В парной линейной зависимости. С помощью корреляционного анализа изучают тесноту взаимосвязи между признаками

С помощью корреляционного анализа изучают тесноту взаимосвязи между признаками. Для этой цели можно было бы использовать коэффициент регрессии, исходя из его экономического смысла, но данный коэффициент имеет размерность. Поэтому преобразуем коэффициент регрессии:

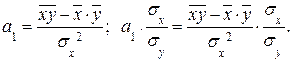
Величина 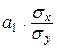размерности не имеет. Эту величину называют линейным парным коэффициентом корреляции. Так как коэффициент корреляции вычисляется по выборочным данным, то его еще называют выборочным линейным коэффициентом корреляции и обозначают 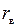. Итак,

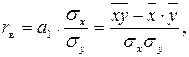
где 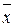, , 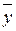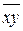- выборочные средние; 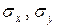- выборочные средние квадратические отклонения.

Из формулы 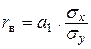выразим .

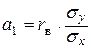Тогда уравнение регрессии можно записать так:

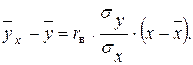
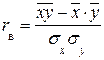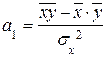Сравнивая формулы расчета и , видим, что эти коэффициенты имеют одинаковые знаки.

Выборочный коэффициент корреляции 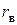является показателем тесноты взаимосвязи между признаками. Этот коэффициент применяют для оценки тесноты связи между признаками Х и У в линейной корреляционной зависимости.

Отметим свойства выборочного коэффициента корреляции:

1) 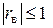, то есть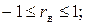

2) чем ближе 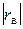к 1, тем взаимосвязь между признаками Х и У будет более тесной, а чем ближе 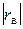к 0, тем взаимосвязь слабее;

3) если 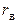= +1, то связь между признаками Х и У линейная функциональная;

4) если r_в <0, то связь между признаками обратная; если r_в >0, связь прямая;

5) если 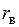=0, то между признаками отсутствует линейная корреляционная зависимость.

Докажем это свойство. Если 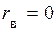, то 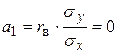, следовательно, уравнение регрессии примет вид 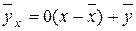, то есть 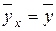. Поэтому линия регрессии будет параллельна оси абсцисс, и с ростом значений Х условная средняя 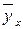не меняется. Отсюда следует, что линейная корреляционная зависимость между признаками Х и У отсутствует, что и требовалось доказать.

Замечание. Равенство 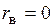говорит лишь об отсутствии линейной корреляционной зависимости, а не об отсутствии корреляционной связи вообще. Между признаками может существовать и нелинейная корреляционная связь (например, параболическая или гиперболическая).

В генеральной совокупности показателем линейной корреляционной связи между признаками Х и У является генеральный коэффициент корреляции .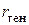

Можно показать, что 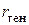вычисляется по формуле

.

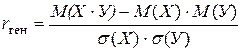Чем ближе 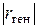к единице, тем теснее линейная связь между признаками Х и У.

Как правило, генеральный коэффициент корреляции 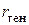неизвестен. О тесноте линейной связи между признаками судят не по величине 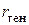, а по величине его выборочного аналога, то есть 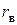. Так как 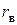вычисляется по значениям переменных, случайно попавшим в выборку, то величина 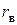меняется от выборки к выборке. Следовательно, в отличие от 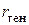, выборочный коэффициент корреляции 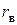- величина случайная. Поэтому 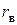является оценкой генерального коэффициента корреляции, то есть .

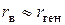Пусть найденный по выборке коэффициент корреляции 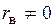. Возникает вопрос: чем объясняется такая величина ?

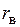Ответов может быть несколько.

1) Действительно существует линейная корреляционная связь между признаками Х и У в генеральной совокупности. Поэтому 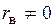отражает тот факт, что и .

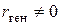2) Вследствие случайности отбора значений признаков в выборку оказалось, что 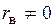. При другом отборе, возможно, 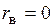или же 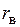изменит свой знак.

Для того чтобы выбрать правильный ответ, следует решить, значимо ли 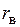, найденный по выборке, отличается от нуля. Если выборочный коэффициент корреляции значимо отличается от нуля, то между признаками Х и У в генеральной совокупности действительно существует линейная корреляционная зависимость. Если же выборочный коэффициент корреляции отличается от нуля незначимо, то можно считать, что линейная корреляционная связь между признаками отсутствует.

Задача эта очень важная, так как линейное уравнение регрессии имеет смысл строить только в том случае, если признаки Х и У находятся в тесной линейной корреляционной зависимости между собой.

С этой целью выдвигаются нулевая и конкурирующая гипотезы:

Н₀: r_ген = 0, Н₁: r_ген № 0.

В этом случае рассматривается двусторонняя критическая область.

Нулевая гипотеза проверяется при заданном уровне значимости a с помощью случайной величины Т,имеющей распределение Стьюдента с k = n - 2 степенями свободы:

.

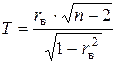По выборочным данным вычисляют Т_набл, а по таблице критических точек распределения Стьюдента находят t_{крит.дв}(a, k) с учетом двусторонней критической области. Сравнивают Т_набл и t_{крит.дв}(a, k).

ЕслиЅТ_наблЅ < t_{крит.дв}(a, k), то есть наблюдаемое значение критерия попало в область принятия гипотезы, то нет оснований отвергать нулевую гипотезу по данным наблюдения r_ген = 0, признаки Х и Y не коррелированы, r_в незначим.

А если Т_набл попало в критическую область, то есть 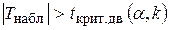, то нулевую гипотезу отвергаем, принимаем конкурирующую Н₁: r_ген № 0, признаки Х и Y коррелированы, r_в значим.

Итак, если r_в оказался значим, то можно найти коэффициент детерминации по формуле D = 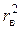Ч 100 % , который показывает, на сколько процентов в среднем вариация результативного признака Y объясняется за счет вариации факторного признака X.

Пример 2. Ранее по корреляционной таблице было установлено, что себестоимость единицы продукции и производительность труда находятся в корреляционной зависимости. Получены следующие данные:

Хi
	13,80	12,20	11,00	9,73	7,67	.

Требуется провести корреляционно-регрессионный анализ.

Решение. Результативный признак У - себестоимость единицы продукции, р. Факторный признак Х - производительность труда, тыс. шт. Предполагаем, что признаки имеют совместный нормальный закон распределения.

Установим форму корреляционной зависимости. С этой целью строим точки с координатами (х_i, у_i) (рис. 5).

Эмпирическая линия регрессии изображена на рис. 5. По расположению построенных точек делаем вывод, что корреляционную связь можно считать линейной. Выборочное уравнение регрессии в общем виде: 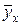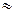a₀ + a₁х. Итак, форма связи линейная.

Проведем корреляционный анализ. Вычислим выборочный линейный коэффициент корреляции:

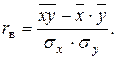
Рис. 5

Будем выполнять расчеты, опираясь на исходную корреляционную таблицу:

Себестоимость единицы продукции,	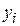Производительность труда,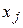

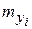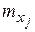При вычислении выборочных характеристик признаков Х и У будем учитывать, что данные сгруппированы. Расчеты удобно представить в следующих таблицах:

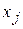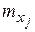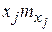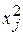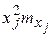Итого

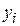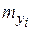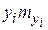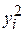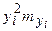Итого

Тогда

;

;

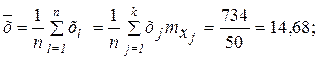
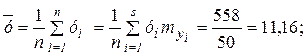
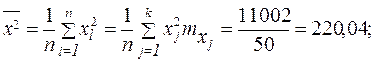
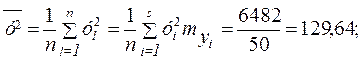
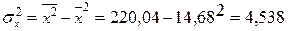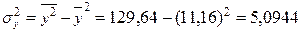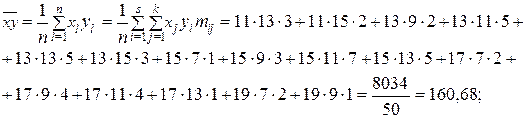
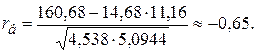
Проверим значимость выборочного коэффициента корреляции. Для этого выдвигаем гипотезы:

Н₀: r_ген = 0, Н₁: r_ген № 0. Примем уровень значимости .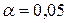

Для проверки нулевой гипотезы используем случайную величину 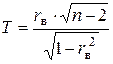, имеющую распределение Стьюдента с k = n - 2 = 48 степенями свободы. По выборочным данным находим наблюдаемое значение критерия Т_набл = 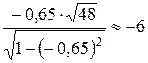. По таблице критических точек распределения Стьюдента находим t_{крит.дв}(0,05; 48) 2,02. Сравниваем Т_набл и t_крит(0,05; 3). Так как ЅТ_наблЅ  t_{крит.дв}(0,05; 3), то есть Т_набл попало в критическую область, нулевая гипотеза отвергается, принимается конкурирующая гипотеза Н₁: r_ген № 0, r_в значим. Признаки Х и Y коррелированы. Так как Ѕr_вЅ достаточно близок к единице, следовательно, себестоимость единицы продукции и производительность труда находятся в тесной корреляционной зависимости.

Найдем коэффициент детерминации. D = r_в² Ч 100 % 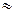42 %, то есть вариация себестоимости единицы продукции в среднем на 42 % объясняется вариацией производительности труда.

Выразим зависимость между этими признаками приближенно в виде линейного уравнения регрессии:

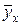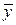- » a₁(х - ),

,

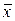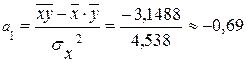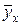- 11,16 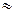- 0,69 (x – 14,68) или 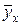» - 0,69x + 21,36.

Отсюда следует, что с увеличением производительности труда на 1 тыс. шт. себестоимость единицы продукции снизится в среднем на 0,69 р.

Найдем по уравнению регрессии себестоимость одного изделия, если производительность труда составит 18 тыс. шт.

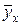» - 0,69 Ч 18+ 21,38 =8,96 (р.).

Пример 3. Для нормирования труда проведено статистическое исследование связи между количеством изготавливаемых изделий (Х, шт.) и затратами времени на обработку одного изделия (Y, мин). Сделана выборка объемом n = 51, и получены следующие данные: r_в = 0,8, 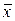= 8, s_x= 3,2, 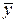= 40, s_y = 8.

Проверить значимость коэффициента корреляции при a = 0,02. Построить уравнение регрессии.

Решение. Признак Х - количество изготавливаемых изделий, шт. Признак Y - затраты времени на обработку одного изделия, мин.

Предполагаем, что признаки имеют нормальный закон распределения. Они находятся в статистической зависимости, так как затраты времени зависят не только от количества изготавливаемых изделий, но и от многих других факторов, которые здесь не учитываются. В данном случае связь между признаками линейная, так как теснота связи характеризуется линейным коэффициентом корреляции r_в = 0,8. Но прежде чем делать вывод о тесноте взаимосвязи, необходимо проверить значимость выборочного коэффициента корреляции. Выдвигаем нулевую гипотезу и ей конкурирующую:

Н₀: r_ген = 0, Н₁: r_ген № 0.

Проверяем нулевую гипотезу с помощью случайной величины, имеющей распределение Стьюдента с k = n - 2 = 49 степенями свободы: .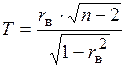

По выборочным данным найдем наблюдаемое значение критерия Т_набл = 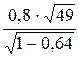» 9,33. По таблице критических точек распределения Стьюдента находим t_{крит.дв}(a, k) = t_{крит.дв}(0,02; 49) = 2,40. Сравниваем Т_набл и t_{крит.дв}(0,02; 49). Так как ЅТ_наблЅ > t_{крит.дв}(0,02; 49), то есть наблюдаемое значение критерия попало в критическую область, нулевая гипотеза отвергается, принимается конкурирующая гипотеза Н₁: r_ген № 0, признаки Х и Y коррелированы, r_в значим.

D = 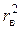Ч 100 % = 64 % , то есть вариация затрат времени на обработку одного изделия в среднем на 64 % объясняется за счет вариации количества изготавливаемых изделий.

Представим эту взаимосвязь аналитически в виде уравнения регрессии вида

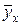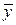- » a₁(х - ).

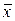Коэффициент a₁ выразим через парный линейный коэффициент корреляции

.

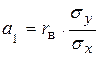Тогда по выборочным данным будем иметь

a₁ = 0,8 Ч 8/32 = 2; 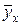- 40 » 2(x - 8) или 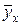» 24 + 2x .

Отсюда следует, что с увеличением количества выпускаемых изделий на 1 шт. затраченное время в среднем увеличится на 2 мин.