Приведение ОБЩЕГО уравнения ЛВП к каноническому виду

ОБЩЕЕ УРАВНЕНИЕ ЛИНИИ ВТОРОГО ПОРЯДКА

1. Уравнения ЛВП с осями симметрии, параллельными координатным осям.

Пусть имеются два прямоугольных репера. Найдем в старом репере уравнение эллипса с центром в точке О¢, полуосями а и b, оси которого параллельны координатным осям, т.е. полученном при параллельном переносе. Пусть координаты нового начала координат О¢(х₀; у₀)_R. Тогда в новом репере уравнение эллипса:

.

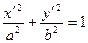По формулам параллельного переноса: 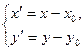получим:

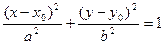. (4)

Раскроем скобки, приведем подобные слагаемые, получим:

.

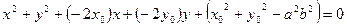Введем соответствующие обозначения для коэффициентов при различных степенях неизвестных, получим уравнения вида:

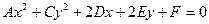(5)

Аналогичные преобразования можно выполнить для гиперболы и параболы. Коэффициенты А и С не равны нулю одновременно.

Теорема 1. Уравнение вида (5) всегда определяет: либо окружность (А=С), либо эллипс (АС>0, т.е. А и С одного знака), либо гиперболу (АС<0, т.е. А и С разных знаков).

Примечание. Возможны случаи, когда эллипс вырождается в точку или мнимый эллипс, гипербола – в пару пересекающихся прямых, парабола – в пару параллельных прямых:

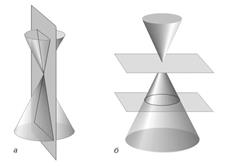
2. Общее уравнение ЛВП, с осями симметрии, не параллельными координатным осям.

Рассмотрим случай расположения ЛВП относительно старого репера, когда ее оси симметрии не параллельны координатным осям, т.е. при повороте. Линии соответствует уравнение:

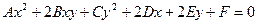(6)

Это уравнение называется общим уравнением линии второго порядка.

Используем формулы поворота: 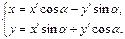Подставим их в уравнение (6) и выполним тождественные преобразования:

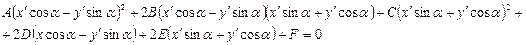
Выберем угол a так, чтобы коэффициенты при 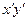обратился в нуль, т.е.

.

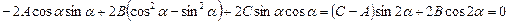Отсюда .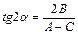

При повороте осей на угол, удовлетворяющий последнему условию, уравнение (6) приведется к уравнению (5).

Вывод. Общее уравнение второго порядка определяет на плоскости линию второго порядка.

Классификация ЛВП

Дано общее уравнение линии второго порядка 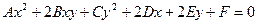(6)

Уравнение (6) всегда определяет линию второго порядка.

Рассмотрим определитель второго порядка .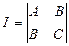

1) Если I>0, то уравнение определяет эллипс 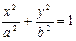, вырожденные случаи: точку (пара мнимых пересекающихся прямых) 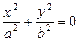и мнимый эллипс .

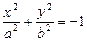2) Если I<0, то уравнение определяет гиперболу 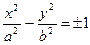, вырожденный случай: пару пересекающихся прямых .

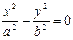3) Если I=0, то уравнение определяет параболу 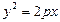, вырожденные случаи: пару действительных параллельных прямых 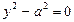, пару мнимых параллельных прямых 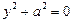, пару совпавших прямых .

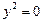Типы ЛВП

Линия	Каноническое уравнение	Дискриминант I	Действительные точки	Центры
1. Эллипс		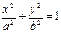+	¥	не на линии
2. Гипербола		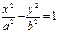–	¥	не на линии
3. Парабола		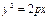	¥	нет
4. Мнимый эллипс		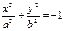+		не на линии
5. Пара пересекающихся прямых		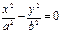–	¥	на линии
6. Пара мнимых пересекающихся прямых		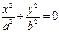+		на линии
7. Пара параллельных прямых		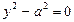	¥	Прямая центров не на линии
8. Пара мнимых параллельных прямых		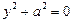		Прямая центров не на линии
9. Пара совпавших прямых		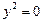	¥	Прямая центров на линии

Приведение ОБЩЕГО уравнения ЛВП к каноническому виду

1 способ. Выделение полного квадрата.

2 способ. Применение формул преобразования координат (с исследованием линии второго порядка).