Демонстрационная задача № 2

Пусть на 12 участках заданного хозяйства получены оценки качества земли и средние для каждого участка урожайности озимой пшеницы (таблица 3). По результатам оценок установить функциональную зависимость урожайности (y) озимой пшеницы от балла оценки земли (x).

Таблица 4

Исходные данные для решения задачи

№ п/п (j)	Балл оценки земель (xj)	Урожайность, ц/га (yj)
		23.5
		23.7
		24.0
		26.7
		24.3
		28.8
		33.5
		27.6
		23.0
		29.4
		30.5
		35.0

Рассчитать показатели, характеризующие тесноту связи между урожайностью и баллом оценки земель, оценить погрешность определения коэффициента корреляции , рассчитать экономические характеристики, определить коэффициент детерминации, стандартное отклонение.

Решение

Для определения зависимости между значением урожайности и баллом оценки земель построим график в двухмерной системе координат (x,y), где у – урожайность озимой пшеницы, х – балл оценки земли (рис. 2).

Рисунок свидетельствует о том, что зависимость урожайности озимой пшеницы от балла оценки земли имеется и близка к линейной.

Рассчитаем коэффициенты для системы нормальных уравнений в случае линейного представления зависимости: y=a₀+ a₁x.

25 30 35 40 45 50 x

Рис. 2 . Графическое представление зависимости между значением урожайности и баллом оценки качества земли

Для получения нормальных уравнений приравняем нулю первые производственные суммы квадратов отклонений случайных величин y^j , полученных в выборках от соответствующих значений 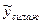по параметрам а₀ и а₁.

, то тогда ;

;

Вид системы нормальных уравнений:

.

Для расчета параметров составим таблицу 5.

Таблица 5

Расчет коэффициентов для системы нормальных уравнений

(случай линейного представления зависимости)

№ п/п j	Балл оценки земель , xj	Урожайность ц/га, yj	(xj)2	xj yj	Сглаженное значение
		23,5		705,0	23,01
		23,7		829,5	25,55
		24,0		840,0	25,55
		26,7		1014,6	27,08
		24,3		704,7	22,50
		28,8		1152,0	28,09
		33,5		1507,5	30,63
		27,6		1021,2	26,57
		23,0		805,0	25,55
		29,4		1176,0	28,09
		30,5		1525,0	33,18
		35,0		1820,0	34,19
S		330,0		13100,5	330,0

С учетом результатов расчетов сумм, представленных в последней строке таблицы, система нормальных уравнений для рассматриваемой задачи будет иметь вид:

Для того, чтобы решить данную систему уравнений, разделим каждое уравнение на коэффициент при a₁. Получим:

Вычтем из второго уравнение первое, получим:

1,206a₁ = 0,613; a₁ = 0,508.

Подставив значение a₁ в любое из уравнений, найдем a₀:

a₀ = 27,5 - 38,833×0,508 = 7,77.

Решение системы:

а₀=7,77;

а₁=0,508.

Линейное представление зависимости урожайности пшеницы от оценки качества земли имеет вид:

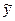=f(x)=7.77+0.508x.

Рассмотрим пример, когда функциональное представление рассматриваемой зависимости ищется в классе полиномов второй степени (парабол. ) y= a₀+ a₁x+a₂x².

По условию задачи № 2 рассчитаем коэффициенты для системы нормальных уравнений - случай полиномиального 2-й степени представления.

Зависимость в классе полиномов 2^ой степени - парабола:

y= a₀+ a₁x+a₂x².

Для определения параметров а₀, а₁ и а₂ решимсистему нормальных уравнений:

Для расчета коэффициентов системы нормальных уравнений (случай полиномиального 2-й степени представления) составим таблицу 6.

Таблица 6

Расчет коэффициентов системы нормальных уравнений

(случай линейного представления зависимости)

j	x	y	x­y	x2	x2y	x3	x4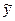
		23,5 23,7 24,0 26,7 24,3 28,8 33,5 27,6 23,0 29,4 30,5 35,0	705,0 829,5 840,0 1014,6 704,7 1152,0 1507,5 1021,2 805,0 1176,0 1525,0 1820,0		21150,0 29032,5 29400,0 38554,8 20436,3 46080,0 67837,5 37784,4 28175,0 47040,0 76250,0 94640,0			23,11 25,52 25,52 27,01 22,64 28,02 30,58 26,51 25,52 28,02 33,23 34,32
S		330,0	13100,5		536380,5			330,01

Решив систему нормальных уравнений:

,

получим a₀=10.3, a₁=0.38, a₂=0.0016.

Сглаженная зависимость урожайности пшеницы от качества земли имеет вид:

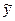= f(x) = 10.3+0.38x + 0.0016x².

Если сравнить значения показателя 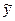, вычисленного по функциональному представлению линейной зависимости (таблица 4) и по представлению квадратичной параболы (таблица 5), то видим незначительные расхождения. Если выбор функциональной зависимости осуществить между этими двумя представлениями, то достаточно ограничиться линейным.