Уравнение прямой в отрезках
Пусть 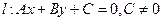 .
.
Преобразуем данное уравнение:
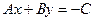 .
.
Поделим уравнение на (-С).
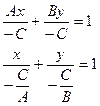
Обозначим 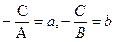 тогда получим уравнение вида
тогда получим уравнение вида
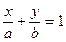 - уравнение прямой в отрезках.
- уравнение прямой в отрезках.
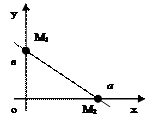 Геометрический смысл уравнения.
Геометрический смысл уравнения.
1 Если х=0, получим 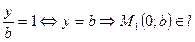 .
.
2 Если у=0, получим 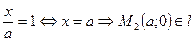 .
.
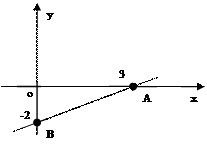 Пример 10 Построить прямую
Пример 10 Построить прямую 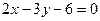 .
.
Решение: Преобразуем данное уравнение к виду 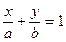
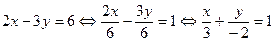
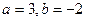 .
.
И проведем через точки А и В искомую прямую.
Угол между двумя прямыми, заданными уравнениями с угловыми коэффициентами. Условия параллельности и перпендикулярности
Пусть 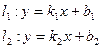
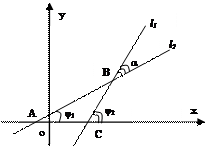 Углом между прямыми l1 и l2 будем называть угол α, на который нужно повернуть прямую l1 против хода часовой стрелки до первого совмещения с прямой l2.
Углом между прямыми l1 и l2 будем называть угол α, на который нужно повернуть прямую l1 против хода часовой стрелки до первого совмещения с прямой l2.
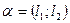
Пусть φ1 – угол наклона прямой l1, к оси ОХ, φ1 – угол наклона прямой l2 к оси ОХ.
Из ΔАВС имеем 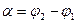 .
.
Следовательно, 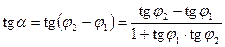 .
.
Но т.к. 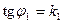 , а
, а 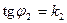 , то последнее равенство можно записать так:
, то последнее равенство можно записать так:
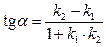 .
.
Следствие:
1 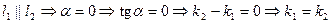
2 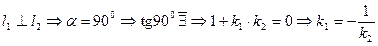
Пример 11Определить угол между прямыми 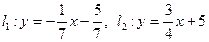
Решение: 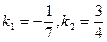 . Тогда по формуле имеем
. Тогда по формуле имеем
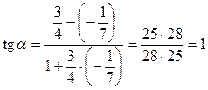 .
.
Следовательно 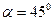 .
.
Рассмотренные уравнения прямой представлены в таблице 1.
Таблица 1 - Уравнения прямой
| Вид уравнения | Название уравнения | |
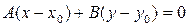 | Уравнение прямой, проходящей через точку с координатами (x0,y0), перпендикулярно вектору 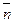 (A,B) (A,B) | |
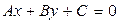 | Общее уравнение прямой | |
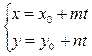 | Параметрические уравнения прямой (уравнение прямой, проходящей через точку с координатами (x0,y0), параллельно вектору 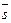 (m,n )) (m,n )) | |
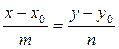 | Каноническое уравнение прямой (уравнение прямой, проходящей через точку с координатами (x0,y0), параллельно вектору 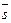 (m,n )) (m,n )) | |
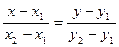 | Уравнение прямой, проходящей через точки с координатами (x1, y1) и (x2, y2) | |
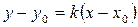 | Уравнение прямой, проходящей через точку с координатами (x0,y0 ), и имеющей угловой коэффициент k. | |
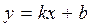 | Уравнение прямой с угловым коэффициентом k и начальной ординатой b | |
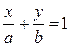 | Уравнение прямой в отрезках (а,в– отрезки на осях х и у) |
Тема 3.2 Кривые второго порядка
План:
1 Основные понятия
2 Окружность
3 Эллипс
4 Гипербола
5 Парабола
1Основные понятия
Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат. В общем случае это уравнение имеет следующий вид:
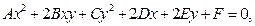
При этом предполагается , что хотя бы один из коэффициентов А, В, С не равно нулю.
Любая линия второго порядка представляет собой либо окружность, либо эллипс, либо параболу, либо гиперболу. Другие случаи линий второго порядка называются вырожденными.
Окружность
Простейшей кривой второго порядка является окружность.
Окружностью называют множество точек плоскости, равноудаленных от заданной точки О на одно и тоже расстояние R. Точка О - центр окружности, R – радиус окружности. Пусть точка О в прямоугольной системе координат Оху имеет координаты 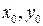 , а
, а 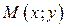 - произвольная точка окружности.
- произвольная точка окружности.
Тогда из условия 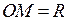 получаем уравнение
получаем уравнение
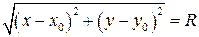
то есть 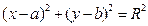 (1)
(1)
Уравнение (1) называется каноническим уравнением окружности. Это уравнение второй степени относительно х и у. Следовательно, окружность есть кривая второго порядка.
Пример 1Найти координаты центра и радиус окружности:
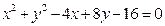 .
.
Решение: Выделяя полные квадраты в левой части данного уравнения, приведем его к виду (1):
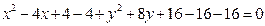 ,
,
т.е. 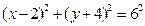 . Центр окружности находится в точке (2;-4), а радиус равен 6.
. Центр окружности находится в точке (2;-4), а радиус равен 6.
Эллипс
Эллипсомназывается множеством всех точек плоскости, сумма расстояний от каждой из каждой из которых до двух данных точек данной плоскости, называемых фокусами, есть величина постоянная, большая расстояния между фокусами.
Обозначим фокусы через 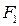 и
и 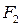 , расстояние
, расстояние 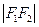 между ними 2с, получим
между ними 2с, получим 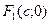 и
и 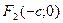 . Постоянную величину, равную сумме расстояний от каждой точки эллипса до фокусов обозначим через 2а (по условию 2а > 2c), М(х;у)- произвольная точка эллипса. Расстояния
. Постоянную величину, равную сумме расстояний от каждой точки эллипса до фокусов обозначим через 2а (по условию 2а > 2c), М(х;у)- произвольная точка эллипса. Расстояния 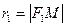 и
и 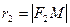 называются фокальными радиусамитолчки М..
называются фокальными радиусамитолчки М..
Пусть дан эллипс. Если оси декартовой прямоугольной системы координат выбраны так, что фокусы данного эллипса располагаются на оси абсцисс симметрично относительно начала координат (рисунок 3), то в этой системе координат уравнение данного эллипса имеет
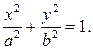 (2)
(2)
где 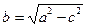 ; очевидно,
; очевидно, 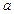 >
> 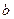 .
.
Уравнение вида (2) называется каноническим уравнением эллипса.
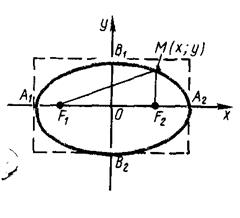
Рисунок 3 - Эллипс, фокусы которого лежат на оси ОХ
Точки А1, А2, В1, В2, пересечения эллипса с осями координат называются вершинами эллипса. Отрезок 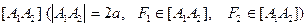 называется большой осью эллипса, а отрезок
называется большой осью эллипса, а отрезок 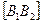
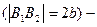 малой осью. Оси
малой осью. Оси 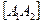 и
и 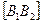 являются осями симметрии эллипса, а точка О – центром симметрии (или просто центром) эллипса.
являются осями симметрии эллипса, а точка О – центром симметрии (или просто центром) эллипса.
Отношение фокального расстояния к длине большой оси называется эксцентриситетом эллипса и обозначается 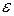 :
:
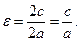 (3)
(3)
Так как с<a, то 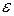 <1 . Эксцентриситет характеризует форму эллипса.
<1 . Эксцентриситет характеризует форму эллипса.
Две прямые, перпендикулярные к Ох и расположенные на расстоянии 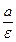 от центра, называются директрисами эллипса:
от центра, называются директрисами эллипса:
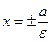 . (4)
. (4)
Если эллипс, определяемый каноническим уравнением, расположен так, что его фокусы лежат на оси Оу, то тогда b> a и большой осью служит отрезок 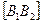 длиной 2b, а малой осью – отрезок
длиной 2b, а малой осью – отрезок 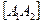 длиной 2а. Эксцентриситет такого эллипса вычисляется по формуле
длиной 2а. Эксцентриситет такого эллипса вычисляется по формуле
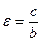 , где
, где 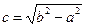 .
.
Эллипс, фокусы которого лежат на оси ОУ, изображен на рисунке 4
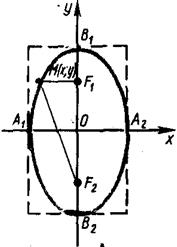
Рисунок 4 - Эллипс, фокусы которого лежат на оси ОУ
Пример 2Дано уравнение эллипса 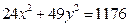 . Найти:
. Найти:
1) длинны его полуосей;
2) координаты фокусов;
3) эксцентриситет эллипса;
4) уравнения директрис и расстояние между ними;
5) точки эллипса, расстояния от которых до левого фокуса F1 равно 12.
Решение: Запишем уравнение эллипса в виде (2), разделив обе его части на 1176:
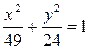 .
.
1 Отсюда 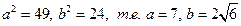 .
.
2 Используя соотношение 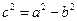 ,
, 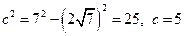 . Следовательно,
. Следовательно, 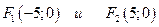
3 По формуле 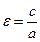 находим:
находим: 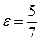
4 Уравнения директрис имеют вид 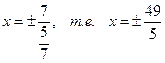 ; расстояние между ними
; расстояние между ними 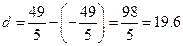
5 По формуле 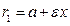 находим абсциссу точек, расстояние от которых до точки
находим абсциссу точек, расстояние от которых до точки 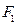 равно 12:
равно 12: 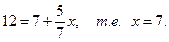 подставляя значения х в уравнение эллипса, найдем ординаты этих точек :
подставляя значения х в уравнение эллипса, найдем ординаты этих точек : 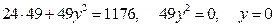 . Условию задачи удовлетворяет точка
. Условию задачи удовлетворяет точка 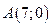
Пример 3Составить каноническое уравнение эллипса, если фокусное расстояние равно 10, а малая ось равна 6.
Решение:По условию задачи
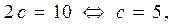
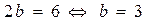 ,
,
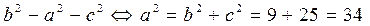 .
.
Следовательно, 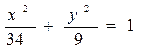 .
.
Гипербола
Гиперболой называется множеством всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек плоскости, называемых фокусами, есть величина постоянная (обозначают 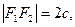 ), меньшая расстояния между фокусами.
), меньшая расстояния между фокусами.
Расстояние между фокусами 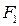 и
и 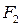 обозначим 2с, а постоянную величину, равную модулю разности расстояний от каждой точки гиперболы до фокусов 2а (0<2а<2с).
обозначим 2с, а постоянную величину, равную модулю разности расстояний от каждой точки гиперболы до фокусов 2а (0<2а<2с).
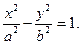 (5)
(5)
уравнение (5) называется каноническим уравнением гиперболы.
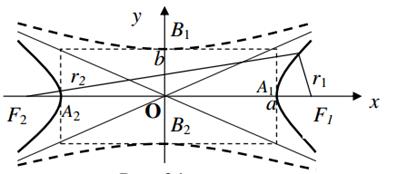
Рисунок 5 - Гипербола, фокусы которой лежат на оси ОХ
Точки А1, А2 пересечения гиперболы с осями координат называются вершинами гиперболы. Отрезок 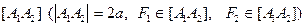 называется действительной осью гиперболы, а отрезок [B1B2]
называется действительной осью гиперболы, а отрезок [B1B2] 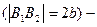 мнимой осью. Оси [A1A2] и [B1B2] являются осями симметрии гиперболы, а точка О– центром симметрии (или просто центром) гиперболы.
мнимой осью. Оси [A1A2] и [B1B2] являются осями симметрии гиперболы, а точка О– центром симметрии (или просто центром) гиперболы.
Эксцентриситет гиперболы 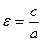 (для гиперболы ε>1).
(для гиперболы ε>1).
Прямые
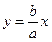 и
и 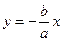 (6)
(6)
Называется асимптотами гиперболы.
Отношение фокального расстояния к длине действительной оси называется эксцентриситетом гиперболы и обозначается 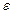 :
:
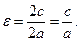 (7)
(7)
Директрисы гиперболы, как и директрисы эллипса, определяются уравнениями
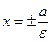 (8)
(8)
Пример 4Дано уравнение гиперболы 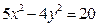 . Найти:
. Найти:
1 Длины его полуосей;
2 Координаты фокусов;
3 Эксцентриситет гиперболы ;
4 Уравнение асимптот и директрис;
5 Фокальные радиусы точки 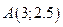
Решение: Разделив обе части уравнения на 20, приведем уравнение гиперболы к каноническому виду
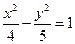 отсюда:
отсюда:
1) 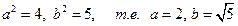
2) используя соотношение 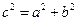 , находим
, находим 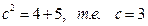 . Отсюда
. Отсюда 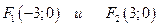
3) По формуле 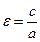 находим:
находим: 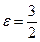
4) Уравнения асимптот и директрис имеют вид 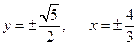 ;
;
5) Точка М лежит на правой ветви гиперболы 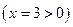 , воспользуемся формулами
, воспользуемся формулами 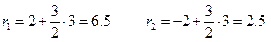
Пример 5 Составьте уравнение гиперболы, вершины которой находятся в точках А (5;0) и В (-5;0), а расстояние между фокусами равно 14.
Решение: По условию задачи имеем: а=5, 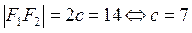 .
.
Найдем 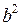 по формуле
по формуле 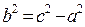 .
.
Получим
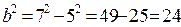 .
.
Следовательно, искомое уравнение имеет вид
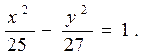
Парабола
Параболой называется множество всех точек плоскости, равноудалённых от данной точки F, называется фокусом, и данной прямой, называемой директрисой.
Обозначим расстояние от фокуса до директрисы p. Эта величина называется параметром параболы.
Уравнение директрисы имеет вид 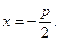
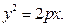 (9)
(9)
Уравнение (9) называется каноническим уравнением параболы.
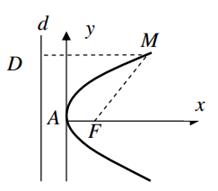
Рисунок 6 - Парабола, фокус которой лежат на оси ОХ
Пример 6Дана парабола 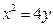 . Найти координаты ее фокуса, уравнение директрисы, длину фокального радиуса точки
. Найти координаты ее фокуса, уравнение директрисы, длину фокального радиуса точки 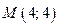 .
.
Решение: Парабола задана каноническим уравнением, значит 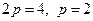 . Используя формулы
. Используя формулы 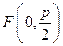 ,
, 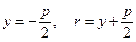 находим , что
находим , что 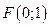 ; уравнение директрисы имеет вид
; уравнение директрисы имеет вид 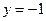 ; фокальный радиус точки М равен
; фокальный радиус точки М равен 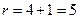 .
.
