Функция для задания комплексного числа по паре действительных чисел в среде Matlab

Алгебраическая форма записи комплексных чисел

Запись числа z в виде z=x+iy является его алгебраической формой записи

Тригонометрическая форма записи комплексных чисел

.

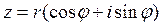Здесь r — модуль комплексного числа (r² = х² + у²), а φ — угол наклона радиус-вектора, проведенного из начала координат в точку (х,у).

Показательная форма записи комплексных чисел

.

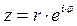Здесь r — модуль комплексного числа (r² = х² + у²), а φ — угол наклона радиус-вектора, проведенного из начала координат в точку (х,у).

Дайте определение суммы и разности двух комплексных чисел

Суммой двух комплексных чисел z₁ и z₂ называется комплексное число вида:

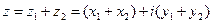
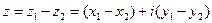
9. Сформулируйте правило умножения и деления комплексных чисел?

Формула умножения двух комплексных чисел, заданных в тригонометрической форме:

;

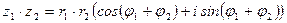Формула умножения двух комплексных чисел в показательной форме

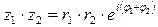
Формула умножения двух комплексных чисел, заданных в алгебраической форме:

;

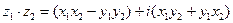Формула деления двух комплексных чисел, заданных в алгебраической форме:

;

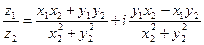Практически частное двух комплексных чисел находят путем умножения делимого и делителя на число, сопряженное делителю

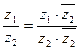
Формула деления двух комплексных чисел, заданных в тригонометрической форме:

;

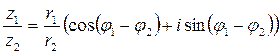Формула деления двух комплексных чисел в показательной форме

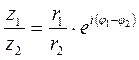
Формула Муавра для возведения в натуральную степень комплексного числа

;

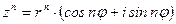Как задать комплексное число в среде Matlab

Запись комплексных величин, используемых в формулах, напоминает общепринятые математические стандарты.

Мнимые части комплексных чисел сопровождаются либо буквой i, либо

буквой j :

>> x=1.2+10i

x = 1.2000 +10.0000i

>> y=3+4j

y = 3.0000 + 4.0000i

Если "переменным" i или j не присвоены какие-либо значения, то их можно применять для формирования комплексных данных, используя знак умножения и располагая такой "сомножитель" до или после мнимой части:

а=1;

x=i*a

х =

0 + l.0000i

y=(i) *а;

У

У =

0 + l.0000i

z=a*i

z =

0 + l.0000i

Однако если i или j представляют настоящие переменные, которым уже присвоены какие-либо значения, то их использование в подобных выражениях не приводит к появлению комплексных данных.

Когда полные комплексные числа используются в операциях умножения, деления или возведения в степень, то для устранения неоднозначности их заключают в круглые скобки:

z=(1.5-0.5i)( 2.5+0.8j)

z =4.1500 - 0.0500i

Функции для выделения мнимой и действительной частей комплексного числа в среде Matlab

С помощью стандартных функций realи imag можно выделить вещественную и мнимую части комплексного значения:

Функция для задания комплексного числа по паре действительных чисел в среде Matlab

Функция complex позволяет сконструировать комплексное значение по паре вещественных чисел:

complex(2,6.6)

ans = 2.0000 + 6.6000i