Дифференциальное исчисление функций одной переменной 3 страница

Пусть 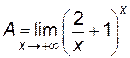. Тогда с учетом того, что логарифмическая функция непрерывна, имеем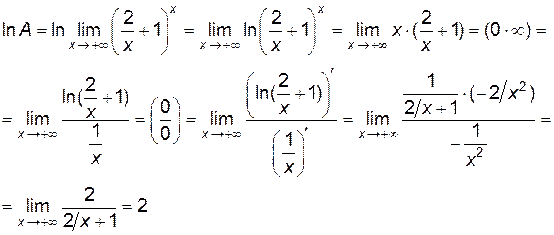

Так как 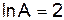, то .

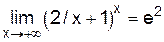7. применение производной для
исследования свойств функций.

7.1. Возрастание и убывание функций

Функция 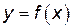называется возрастающей (убывающей) на некотором интервале 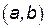, если большему значению аргумента из этого интервала соответствует большее (меньшее) значение функции, т. е. при 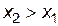выполняется неравенство .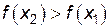

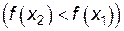Интервалы, в которых функция возрастает или убывает, называются интервалами монотонности функции.

Рассмотрим применение производной для нахождения интервалов монотонности функций.

Теорема 1 (достаточное условие возрастания функции). Если функция 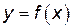непрерывна на отрезке 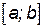и дифференцируема на интервале 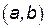, причем 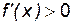( 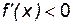) для любого 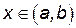, то эта функция возрастает (убывает) на отрезке .

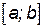Пример 7.1. Исследовать на монотонность (т. е. возрастание и убывание) функцию: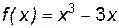

Решение.

.

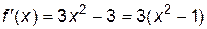Неравенство 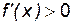, т. е. 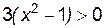, справедливо для x<–1 и для x>1. Следовательно, функция 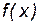возрастает на интервалах (–¥, –1)
и (1, +¥).

Поскольку неравенство 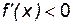, т. е. 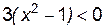справедливо для

xÎ(–1, 1), то на интервале (–1, 1) функция 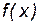убывает.

7.2. Экстремумы функции

Дадим точные определения точкам максимума и минимума функции. Пусть функция 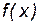определена на промежутке X и x₀ÎX. Говорят, что в точке x₀ функция 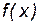имеет максимум (минимум), если существует такая окрестность точки x₀, что для любого x из этой окрестности ( ).

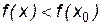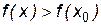Точки максимума и минимума называются точками экстремума.

Замечание 1. Точки экстремума всегда являются внутренними точками промежутка, т. е. не могут быть его концом.

Теорема 2 (необходимое условие экстремума). Если функция 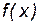дифференцируема в точке x₀ и некоторой ее окрестности и x₀ – точка экстремума, то .

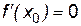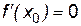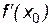Следствие. Если x₀ – точка экстремума, то или не существует.

В качестве примера приведем функцию 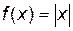(рис. 3).

Рис. 3

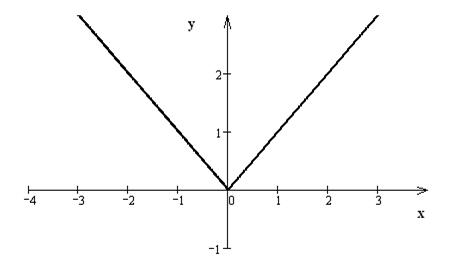
Очевидно, что x₀ = 0 является точкой минимума, так как |0|<|x| для любого x ≠ 0. А в точке x₀ = 0 производной 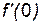не существует.

Если 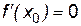или f'(x₀) не существует, то точку x₀ будем называть критической (или подозрительной на экстремум). Критическая точка может и не быть точкой экстремума.

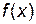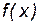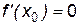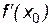Теорема 3 (первое достаточное условие экстремума). Пусть функция определена и непрерывна в точке x₀ и некоторой ее окрестности, дифференцируема в этой окрестности, за исключением, быть может самой точки x₀, и точка x₀ – критическая точка для функции (т. е. или не существует). Тогда:

1) если при x < x₀ производная 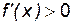, а для x > x₀: 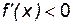, то x₀ – точка максимума;

2) если при x < x₀: 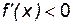, а при x > x₀: 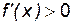, то x₀ – точка минимума.

Пример 7.2. Исследовать на монотонность и экстремумы функцию 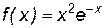. Построить её график.

Решение.

Заданная функция определена и непрерывна на всей числовой оси 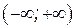. Найдем производную: .

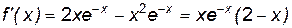Тогда 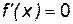при x₁=0 и x₂ =2. Точки x₁, x₂ – критические точки. Эти точки разбивают всю числовую ось на три интервала: (–¥; 0), (0; 2),
(2; +¥). Составим таблицу, в первой строке которой поместим указанные точки и интервалы, во второй строчке – сведения о производной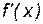
в точках и на интервалах, а в третьей – поведение данной функции 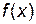(табл. 2).

Таблица 2

x		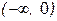	(0, 2)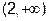
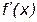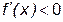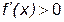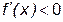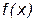	убывает		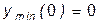возрастает		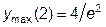убывает

Определим знак 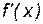на каждом из интервалов: если xÎ(–¥, 0), то 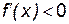; если xÎ(0, 2), то 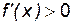; если xÎ(2, +¥ ¥), то 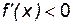. Отсюда определяется поведение функции 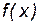: на первом и последнем интервалах функция 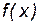убывает, а на втором – возрастает (рис.4).

y(x)=x2e-x

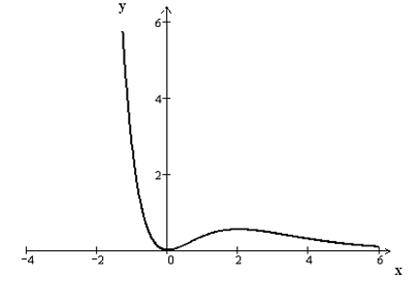
Рис. 4

Отсюда следует, что x₁ = 0 является точкой минимума, ,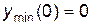
а x₂ =2 – точка максимума, .

7.3. Наибольшее и наименьшее значения функции на отрезке

Известно, что если функция непрерывна на отрезке, то она достигает на этом отрезке своего наименьшего и наибольшего значения. Иногда требуется найти наименьшее или наибольшее значение такой функции.

Если на отрезке 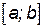есть точки минимума и максимума функции 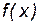, то наименьшее значение функция будет принимать либо в одной из точек минимума, либо на конце отрезка 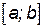. Аналогично для наибольшего значения.

Сформулируем алгоритм нахождения наибольшего и наименьшего значения функции f(x), непрерывной на отрезке:

1. Найти критические точки x₁, x₂, ..., x_n функции 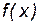. Для этого необходимо решить уравнение .

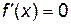2. Отобрать все критические точки, принадлежащие отрезку .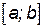

3. Вычислить значения функции 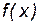в этих критических точках и на концах отрезка.

4. Из этих значений выбрать самое большое и самое малое. Эти числа и будут наибольшим и наименьшим значениями 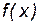на отрезке .

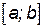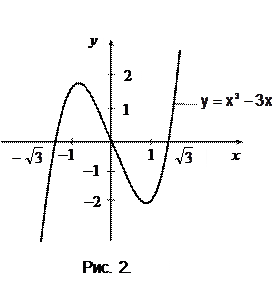
Пример 7.3. Найти наименьшее и наибольшее значения функции

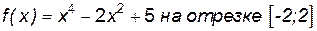
Решение.

1. Найдем критические точки для данной функции:

;

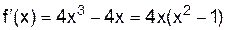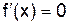при x₁=0, x₂ =–1, x₃ =+1.

2. Все три критические точки принадлежат данному отрезку.

3. Вычислим значения функции в точках: :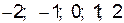

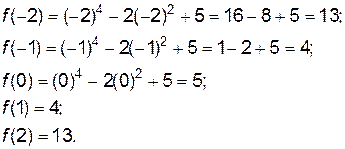
4. Из найденных значений самое малое число 4, а самое большое число 13.

Таким образом, наименьшее значение функции равно 4, в точке х = 1, наибольшее значение равно 13, в точке х = 2 и в точке х = -2.

Пример 7.4. Найти наибольшее и наименьшее значения функции

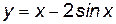на отрезке .

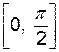Решение.

1. 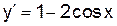, 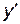определена во всех точках; 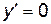при .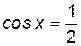

2. На отрезке 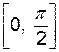, 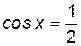при .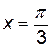

3. Имеем три точки: 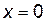, , 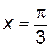, 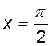в которых может достигаться наибольшее и наименьшее значения.

;

;

.

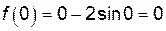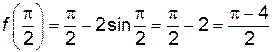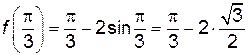Итак, , .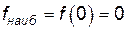

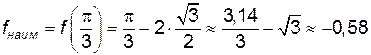Пример 7.5. Найти наибольшее и наименьшее значения функции

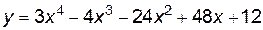на отрезке .

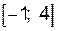Решение.

1. Найдем критические точки функции из условия, что 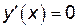или такие, при которых 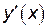не существует:

.

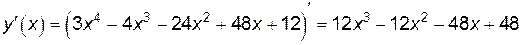Производная 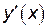во всех точках существует, 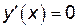, когда .

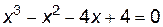Раскладывая левую часть на множители, получаем:

.

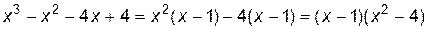Отсюда находим критические точки: , , .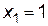

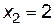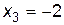2. Из этих точек отрезку 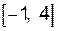принадлежат только две: 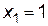и .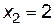

3. Найдем значения функции в этих точках и на концах отрезка, т. е. при , , , :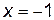

;

;

= ;

.

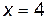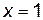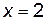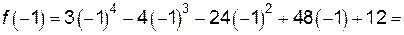
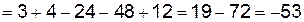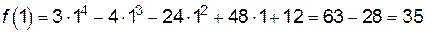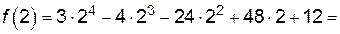
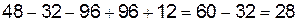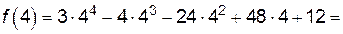
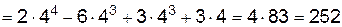Итак, получили , .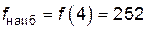

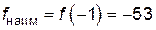Среди многих применений производной функции одной переменной важное значение имеет решение так называемых задач на максимум (минимум).

Пример 7.6. Найти прямоугольный треугольник наибольшей площади, у которого сумма катета и гипотенузы равна .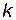

Решение.

Обозначим один из катетов треугольника через 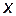, тогда гипотенуза будет равна 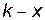, а другой катет, по теореме Пифагора будет равен:

.

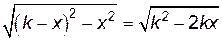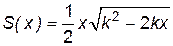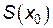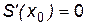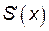Площадь треугольника , так как должна быть максимальной, то или не существует. Находим производную:

.

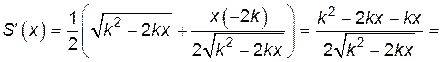
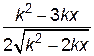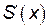не существует, если 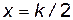, но тогда катет окажется равным гипотенузе, что невозможно. 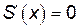, если 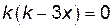. Тогда .

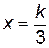Проверяем является ли эта точка точкой максимума. При 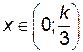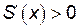, а при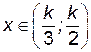 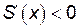. Таким образом при 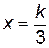площадь треугольника будет наибольшей.

Гипотенуза будет равна 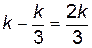, т. е. 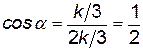, где
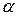– угол, прилежащий к катету 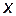. Значит, 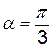; другой угол будет .

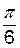Следовательно, искомый треугольник – это прямоугольный треугольник с углами 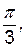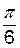и сторонам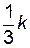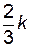и , и .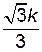

Пример 7.7. Из трех одинаковых досок изготовить симметричный желоб с наибольшей площадью поперечного сечения.

Решение.

Ширину данных досок обозначим через 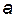. Поперечное сечение желоба изображено на рис. 5,.

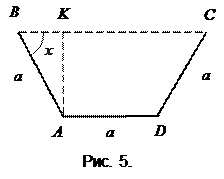
Обозначим через 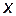угол 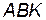( 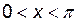), тогда , .

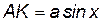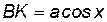Площадь поперечного сечения (площадь трапеции) будет:

.

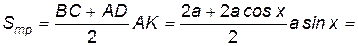
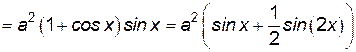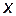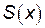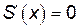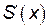Наибольшее значение эта функция принимает в точке максимума, а необходимым условием того, что точка является точкой максимума функции , является то, что или не существует. Найдем :

.

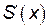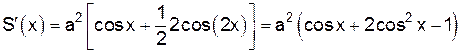Но 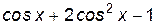всегда существует. Точки, в которых 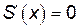, находятся из уравнения: 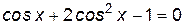. Тогда 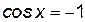или 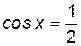. Если 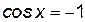, то .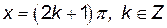

Но в этом случае никакого желоба не получится, так как 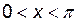. Остается случай, когда, 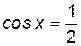, тогда 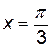, так как .

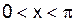Проверим, является ли эта точка 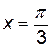точкой максимума функци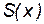и . При 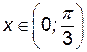, производная функции принимает положительные значения, а при 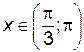- отрицательные. То есть при 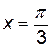площадь поперечного сечения желоба будет наибольшей.

Таким образом, 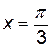действительно точка максимума. А площадь поперечного сечения составит

.

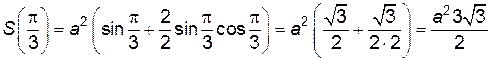7.4. Выпуклость, вогнутость графика функции, точки перегиба

Пусть 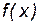– функция, дифференцируемая на интервале 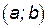. Рассмотрим кривую, являющуюся графиком функции .

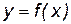Кривая, заданная функцией 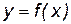, называется выпуклой на интервале 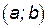, если все точки кривой лежат ниже любой ее касательной на этом интервале.

Кривая называется вогнутой на интервале 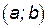, если все точки кривой лежат выше любой ее касательной на этом интервале.

Точка кривой M₀(x₀, f(x₀)), отделяющая выпуклую ее часть от вогнутой, называется точкой перегиба.

Теорема 4 (достаточные условия выпуклости и вогнутости графика функции). Если во всех точках интервала 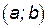вторая производная функции 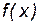отрицательна, т. е. 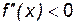, то кривая 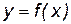на этом интервале выпукла; если во всех точках интервала 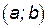– 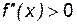, то кривая 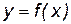на этом интервале вогнута.

Пример 7.8.Определитьнаправление выпуклости и точки перегиба кривой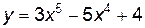

Решение.

Ищем точки х из области определения функции, в которых 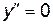или не существует.

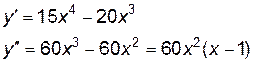
Вторая производная равна нулю 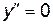в точках 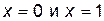. Эти точки являются искомыми, так как область определения и область непрерывности данной кривой есть вся ось абсцисс. Других точек х, которые могли бы быть абсциссами точек перегиба, нет, так как 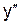существует всюду.