Базисы и размерность линейного пространства.

Размерность. Определение. Если существует натуральное число n такое, что X содержит линейно независимую систему из n векторов, а любая система из n + 1 вектора линейно зависима, то X называется n–мерным линейным пространством, а число n – его размерностью.

Будем обозначать n –мерное линейное пространство X_n , где n = dimX_n — размерность пространства X_n .

Из определения следует, что размерность линейного пространства равна максимальному количеству линейно независимых векторов.

Базис.

Определение. Упорядоченная система векторов e₁, e₂, … , e_n  X называется базисом в X , если

• система векторов e₁, e₂, … , e_n линейно независима;
• любой вектор x пространства X может быть представлен в виде

x = ξ1e1 + ξ2e2 + … + ξnen.

(1)

• Выражение (1) называется разложением вектора x по базису e₁, e₂, … , e_n .
• Коэффициенты ξ₁, ξ₂, … , ξ_n в разложении векторапо данному базису определяются однозначно.

40. Комплексные числа, основные понятия, определения.

Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:

1. Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда

a = c и b = d.

1. Суммой двух комплексных чисел a + ib и c + id называется комплексное число

a + c + i(b + d).

1. Произведением двух комплексных чисел a + ib и c + id называется комплексное число

ac – bd + i(ad + bc).

Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z. Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z. Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел.

Заметим, что арифметические операции над комплексными числами вида z = a + i · 0 осуществляются точно так же, как и над действительными числами. Действительно,

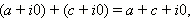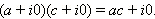Следовательно, комплексные числа вида a + i · 0 естественно отождествляются с действительными числами. Из-за этого комплексные числа такого вида и называют просто действительными. Итак, множество действительных чисел содержится в множестве комплексных чисел. Множество комплексных чисел обозначается 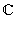. Мы установили, что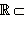 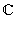, а именно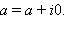

В отличие от действительных чисел, числа вида 0 + ib называются чисто мнимыми. Часто просто пишут bi, например, 0 + i3 = 3i. Чисто мнимое число i1 = 1i = i обладает удивительным свойством:

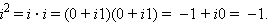Таким образом: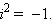

С учётом этого замечательного соотношения легко получаются формулы сложения и умножения для комплексных чисел. Нет нужды запоминать сложную формулу для произведения комплексных чисел – если на комплексные числа смотреть как на многочлены с учётом равенства 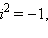,то и перемножать эти числа можно как многочлены. В самом деле,

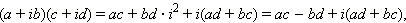то есть как раз получается нужная формула.