Программная реализация метода
Математическое описание метода.
Метод Монте-Карло состоит в том, что рассматривается некоторая случайная величина ξ, математическое ожидание которой равно искомой величине z, т.е.
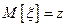
Осуществляется серия n независимых испытаний, в результате которых получается (генерируется) последовательность n случайных величин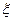 
: 
, 
, …, 
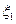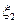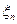и по совокупности этих значений приближенно определяется искомая величина, т.е.
.
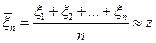Интеграл же может быть вычислен как математическое ожидание некоторой случайной величины ξ, которая определяется независимыми реализациями ηi случайной величины ηс равномерным законом распределения. Двукратные интегралы вычисляются следующим образом:
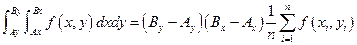, (1)
где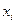 
, 
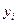– независимые реализации равномерно распределенных на 
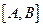величин.
Для использования метода Монте-Карло при вычислении определенных интегралов, как и в других его приложениях, необходимо вырабатывать последовательности случайных чисел с заданным законом распределения. Существуют различные способы генерирования таких чисел. В настоящее время наиболее распространенный способ выработки случайных чисел на ЭВМ состоит в том, что в памяти хранится некоторый алгоритм выработки таких чисел по мере потребности в них. Поскольку эти числа генерируются по наперед заданному алгоритму, то они не совсем случайны (псевдослучайны), хотя и обладают свойственными случайным числам статистическими характеристиками. То есть случайные величины, равномерно распределенные на отрезке 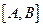, в ЭВМ задаются с помощью специальных программ – генераторов псевдослучайных чисел.
Алгоритм метода в программе:
1. Ввод количества испытаний n.
2. Запустить генератор случайных чисел.
3. Определение общих пределов интегрирования.
4. Случайным образом (с учетом общих пределов интегрирования) генерировать значения x и y.
5. Если значения x и y лежат в текущих пределах интегрирования, то к значению интеграла прибавить значение функции при этих значениях.
6. Пункты 4 и 5 повторить n раз.
7. Окончательно полученную сумму (из формулы 1) перемножить на оставшиеся части формулы (1) для получения значения интеграла.
Описание основных значений в программе.
| n | Количество испытаний |
| DInt | Основная подпрограмма |
| F | Функция для вычисления значений точек подынтегральной функции |
| x, y | Аргументы функции |
| S | Текущее значение суммы (интеграла) |
| Ax, Ay, Bx, By | Пределы интегрирования |
| i | Счетчик |
В программе MonteKarlo используются стандартные модули WinCrt, Strings. В программе MonteKarlo описан метод Монте-Карло, который осуществляется с помощью функций: function F(x,y: real): real; - расчет значения функции и function DInt(A: real; n: longint): real; - вычисление двойного интеграла.
Инструкция по работе с программой.
Для начала работы программы запустить файл MonteKarlo.pas. Код программы.
program MonteKarlo;
uses WinCrt,Strings;
{Расчет значения функции}
function F(x,y: real): real;
begin
F:= exp(x+y)+exp(x-y)*sin(x);
end;
{Подпрограма вычисления двойного интеграла}
function DInt(n: longint): real;
var
S, x, y, Ax, Ay, Bx, By: real;
i: longint;
begin
randomize;
Ax:= 0; Bx:= 4; Ay:= 1; By:=5;
S:=0;
for i:= 1 to n do begin
x:= Ax+random*(Bx-Ax);
y:= Ay+random*(By-Ay);
if ((x>=0) and (x<=4))and((y>=1) and (y<=5)) then S:= F(x,y)+S;
end;
DInt:= (Bx-Ax)*(By-Ay)*S/n;
end;
var
a: real;
n: longint;
BEGIN
StrCopy(WindowTitle, 'Программа вычисления двукратного интеграла методом Монте-Карло');
ClrScr;
WriteLn;
WriteLn(' 5 4');
WriteLn(' / / ');
WriteLn(' Интеграл | | (exp(x+y)+exp(x-y)*sin(x)dxdy');
WriteLn(' / / ');
WriteLn(' 1 0');
WriteLn;
WriteLn;
WriteLn;
Write(' Введите количество вычисляемых значений подынтегральной функции n = ');
ReadLn(n);
WriteLn;
WriteLn;
WriteLn(' Подожтите пожалуйста некоторое время, пока программа произведет расчеты...');
WriteLn;
WriteLn;
WriteLn(' Результаты расчета:');
WriteLn;
WriteLn(' Значение интеграла I = ',DInt(n):10:4);
ReadKey;
DoneWinCrt;
END.
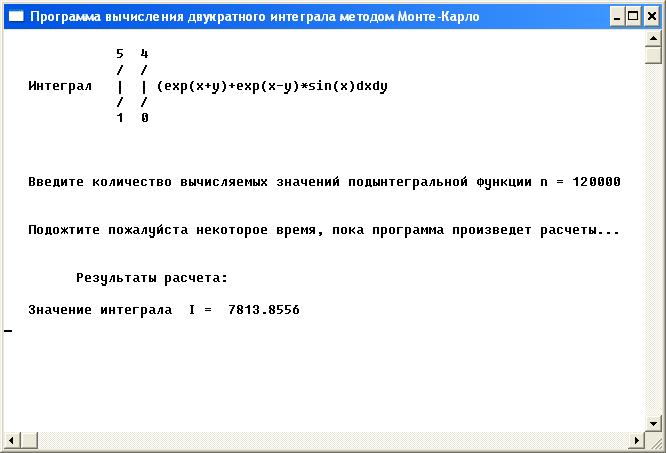
Запустите программу меню Run 
Run или Ctrl+F9, перед вами появится окно:
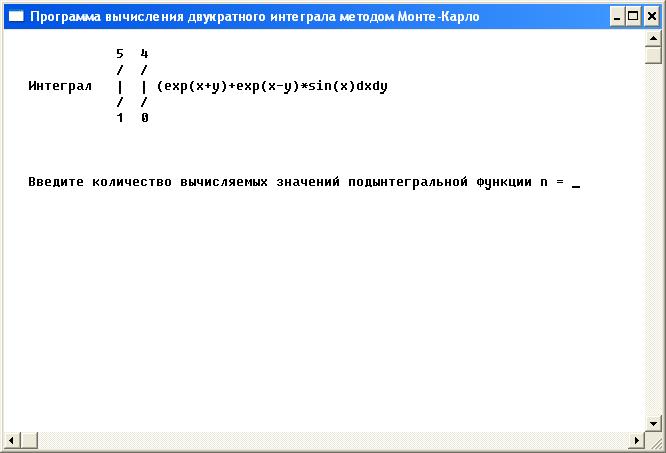
Необходимо ввести количество испытаний n. После этого будет получен результат.
Результат программы.
