Физический смысл производной.

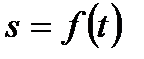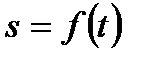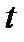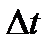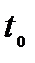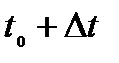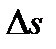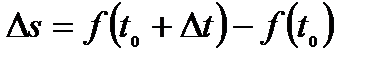Предположим, что функция описывает закон движения материальной точки по прямой линии, т.е. - путь, пройденный точкой за время . За малый промежуток времени от момента до момента материальная точка пройдет путь, равный , где и средняя скорость движения за время 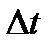составляет .

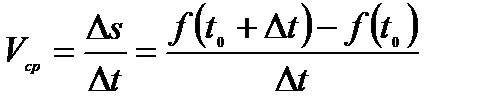Средняя скорость не характеризует состояние движения в определенные моменты времени, а является обобщенной характеристикой движения на промежутке времени .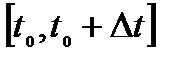

Реальная механическая система за малый промежуток времени мало меняет свои параметры. В частности, средняя скорость за малый промежуток времени приближенно равна мгновенной или истинной скорости движения, и чем меньше промежуток времени, тем ближе средняя скорость к мгновенной и в пределе дает скорость движения в данный момент времени (мгновенная скорость). Таким образом, 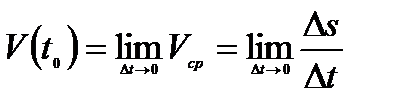, т.е. физический смысл производной состоит в следующем: производная 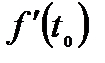функции 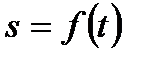в момент времени 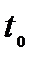равна мгновенной скорости движения, определяемого законом движения 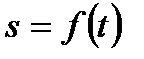, т.е. 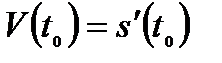или .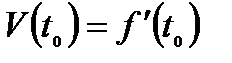

Заметим, что между понятиями непрерывности и дифференцируемости функции в точке существует определенная связь. А именно, если функция 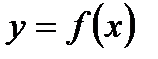дифференцируема в данной точке 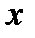, то она непрерывна в этой точке. Обратное утверждение неверно. Функция может быть непрерывной в точке, но не иметь производной в этой точке. Например, функция 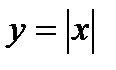является непрерывной в точке 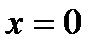, так как

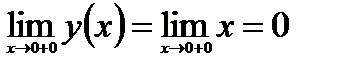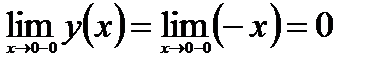, и ,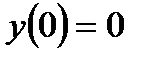

однако производной в этой точке функция не имеет, так как

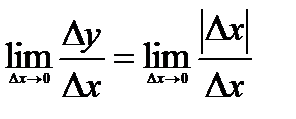не существует, так как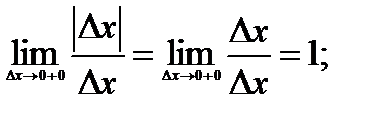 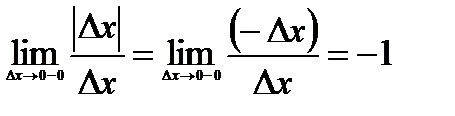, а это и означает, что функция 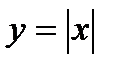в данной точке производной не имеет.

Правила дифференцирования функций.

Пусть функции 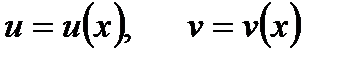дифференцируемы в точке 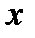, – постоянная. Тогда:

1. ;

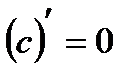2. ;

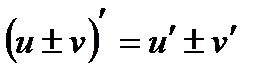3.

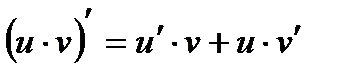
В частности, 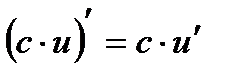, т.е. постоянный множитель можно выносить за знак производной.

4. .

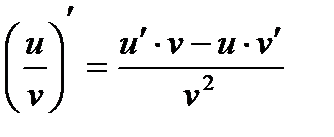
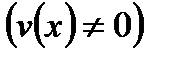Производные основных элементарных функций:

1.		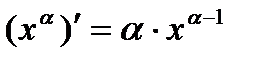8.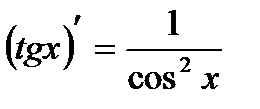
2.		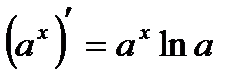9.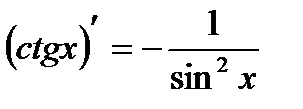
3.		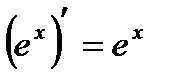10.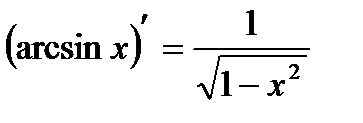
4.		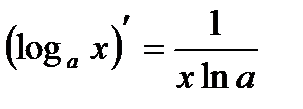11.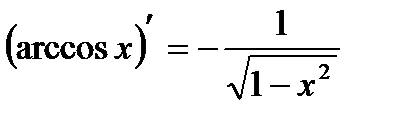
5.		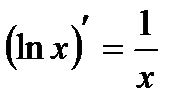12.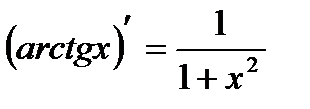
6.		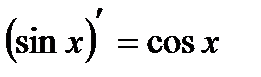13.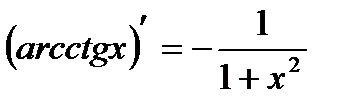
7.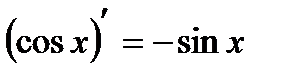

Производная сложной функции.

Если 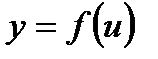, аргумент которой 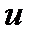является в свою очередь, функцией независимой переменной , т.е. 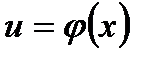, где функци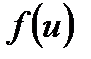и и 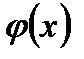имеют производные, то 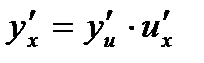- правило дифференцирования сложной функции.

Таким образом, производная сложной функции по независимой переменной равна её производной по промежуточной переменной, умноженной на производную промежуточной переменной по независимой переменной.

Пример 1. Применяя формулы и правила дифференцирования, найти производные следующих функций:

1)

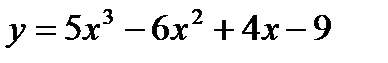
2)

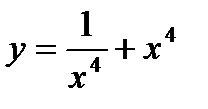
3)

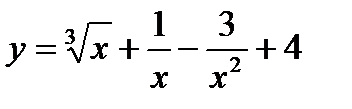
4)

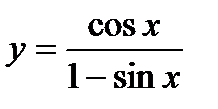
5)

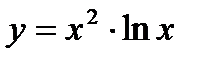
Решение:

1) ;

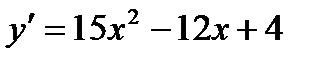2) ;

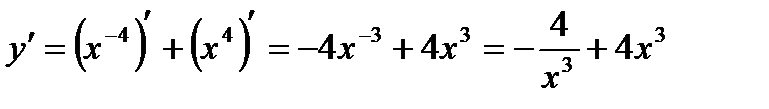3) ;

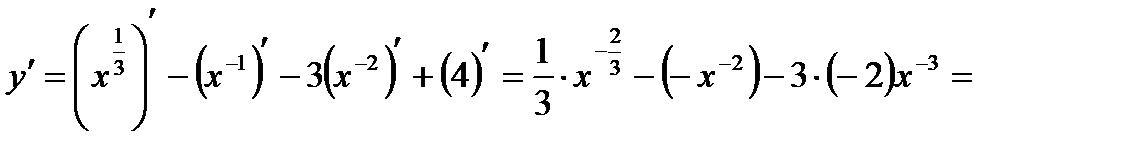
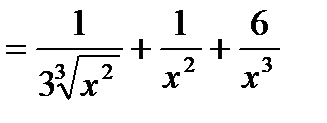4) ;

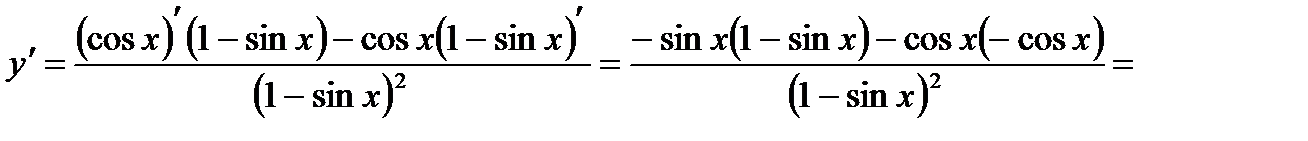
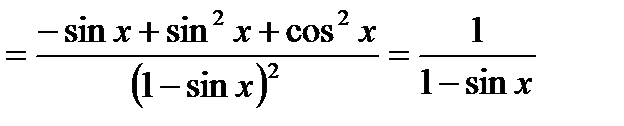5) .

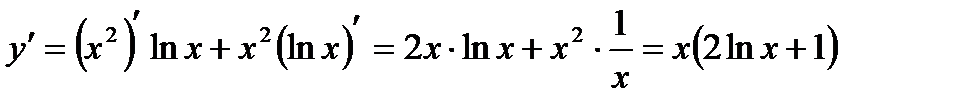Пример 2. Найти производные следующих сложных функций:

1)

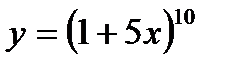
2)

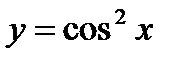
3)

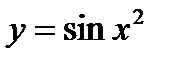
4)

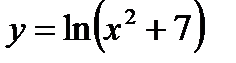
5)

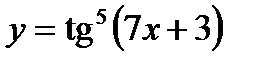
6)

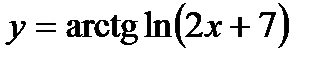
Решение:

1) Обозначим 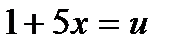, тогда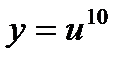
;

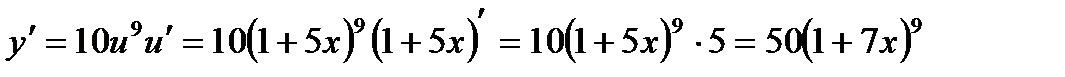2) Полагая 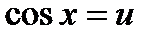, получится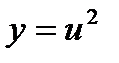
;

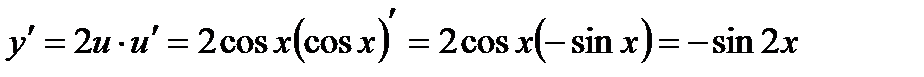3) При 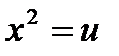, имеем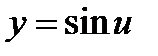
;

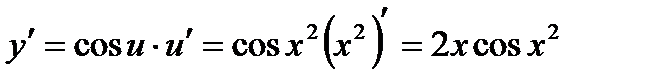4) ;

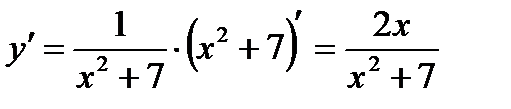5)
;

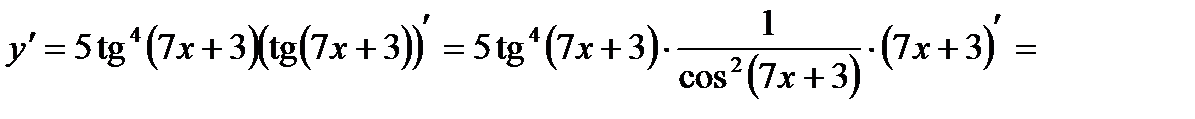
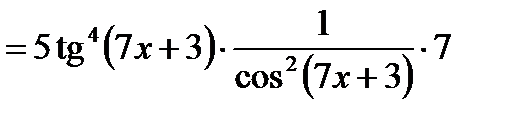6) .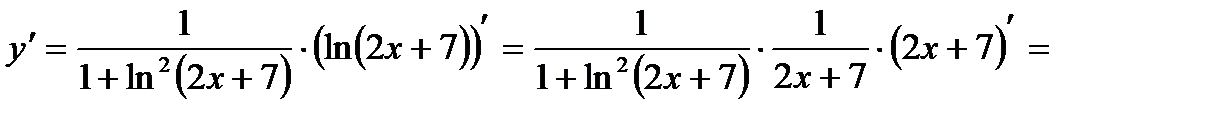
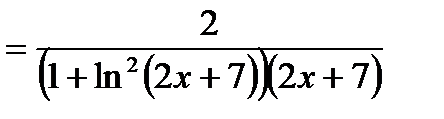