Дифференциальные уравнения первого порядка. Теорема о существовании и единственности решения

Определение

Уравнение вида

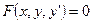(8.2.1)

Где x – независимая переменная, y и y’ – соответственно неизвестная функция и ее производная, называется дифференциальным уравнением первого порядка.

Примеры дифференциальных уравнений первого порядка:

, , .

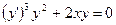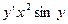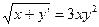В случае, когда из этого уравнения можно выразить 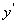, оно имеет вид

.

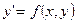(8.2.2)

Уравнение (8.2.2) называется уравнением первого порядка, разрешенным относительно производной. В дальнейшем мы будем рассматривать уравнения первого порядка именно такого вида.

Примерыуравнений, разрешенных относительно производной:

, , .

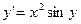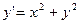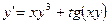Примерыуравнений, которые можно разрешить относительно производной:

1. 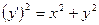, откуда получаем два уравнения первого порядка: .

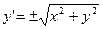2. 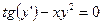, откуда .

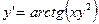3. 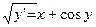, откуда .

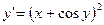Существование и единственность решения дифференциального уравнения

Определение

Решением дифференциального уравнения первого порядка называется функция 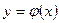, определенная на некотором интервале 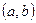, которая при подстановке уравнение (8.2.1) обращает его в тождество.

В теории дифференциальных уравнений основной задачей является вопрос о существовании и единственности решения. Ответ на него дает Теорема Коши, которую мы при водим без доказательств.

Теорема: (Теорема Коши). Пусть дано дифференциальное уравнение (8.2.2). Если функция 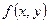и ее частная производная 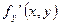непрерывны в некоторой области 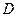плоскости 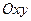, тогда:

Для любой внутренней точки 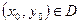найдется решение уравнения (8.2.2), удовлетворяющее условию 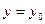при .

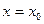Если два решения 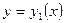и 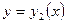уравнения (8.2.2) совпадают хотя бы для одного значения 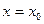, т.е. 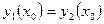, то эти решения совпадают для всех .

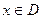При соблюдении условий теоремы Коши через каждую внутреннюю точку области 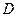проходит только одна интегральная кривая. Условия, которые задают значение функции 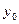в фиксированной точке 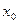, есть начальные условия (или условия Коши) и записываются в такой форме:

.

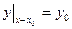(8.2.3)

Задача нахождения решения уравнения (8.2.2), удовлетворяющих условию (8.2.3) называется задачей Коши или иными словами – из множества интегральных кривых выделяется та, которая проходит через заданную точку 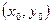области .

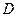В ряде случаев, когда условия теоремы Коши не выполнены, через некоторые точки плоскости 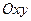либо не проходит ни одна интегральная кривая, либо проходит более одной интегральной кривой. Эти точки называются особыми точками данного дифференциального уравнения.

Приведем пример использования теоремы Коши.

Пример:

Решить уравнение

.

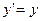(8.2.4)

Решение

В данном случае 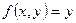, 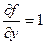определены и дифференцируемы при любых 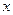и 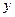. Следовательно, условия теоремы выполнены на всей плоскости .

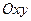Функция 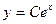является решением уравнения. Покажем, что это решение является общим решением уравнения (8.2.4). Пусть существует какое–либо другое решение уравнения (8.2.4) 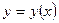. Пусть 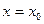– точка, в которой это решение определено, и 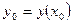. Положим, что 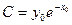, тогда 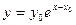. В этом случае решения уравнения (8.2.4) совпадают в точке 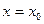. Следовательно, решение уравнения (8.2.4) единственно при конкретном значении константы .

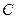Определение

Общим решением уравнения (8.2.2) называется функция 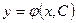, удовлетворяющая этому уравнению при произвольном значении постоянной .

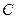Определение

Частным решением уравнения (8.2.2) в области Dназывается функция 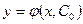, полученная при определенном значении постоянной .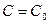