Координаты вектора и точки на плоскости

Пусть на плоскости заданы два неколлинеарных вектора , и произвольная точка O. Пару B = {, } назовем базисом, а тройкуR = {O, , } – аффинным репером. Пусть – произвольный вектор. Отложим все векторы из точки O:

= , = , = .

Проведем прямые l₁= OA , l₂ = OB. Построим параллелограмм, две стороны которого лежат на прямых l₁, l₂, так чтобы C являлась его вершиной. Пусть A₁ и B₁ – вершины параллелограмма, лежащие на l₁ и l₂ соответственно. Пусть = , = . Тогда по правилу параллелограмма = + . Поскольку ||, а ||, то существуют такие числа x₁, x₂ , что = x₁ , = x₂ Þ

= x₁ + x₂. (4)

Это выражение называется разложением векторапо базису B = {, }. Числа x₁, x₂ называются координатами вектора в данном базисе. Они же называются координатами точки C относительно репера R = {O, , }. Пишем (x₁, x₂)_B, C(x₁, x₂)_R. Если заранее известно, о каком базисе или репере идет речь, то их обозначение к координатам не добавляют. Репером на плоскости также называют тройку точек {O, A, B}.

Точка O называется началом координат. Прямые l₁, l₂ вместе с выбранными на них направленными отрезками , называются координатными осями. А совокупность координатных осей и начала координат называется аффинной системой координат (СК) на плоскости. Иногда репером называют также тройку точек {O, A, B}, не лежащих на одной прямой.

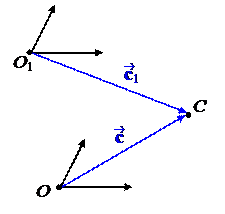Вектор называется радиус-вектором точки C в данной СК или в данном репере. Если мы выберем другое начало координат O₁, то та же самая точка C будет задаваться другим радиус-вектором = . Поэтому ее координаты изменятся. Координаты же вектора не зависят от выбора начала координат.

Действительно, пусть мы имеем еще одно разложение:

= y₁ + y₂, (4¢)

где, например, x₂ ≠ y₂ . Вычтем (4¢) из (4):

= (x₁ – y₁) + (x₂ – y₂) Þ = .

Мы получили, что ||, но мы с самого начала предполагали, что векторы и неколлинеарны. Противоречие. Значит, x₂ = y₂. Аналогично доказывается, что x₁ = y₁.

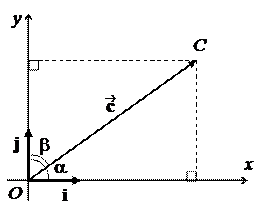Определение. БазисBи реперRназываются ортонормированными, если базисные векторы являются единичными и взаимно перпендикулярными (| |= | |=1 и · = 0). В этом случае СК тоже называется ортонормированной. Если, к тому же, пара (, ) является правой, то СК называется декартовой.

Тогда приняты следующие обозначения: координаты (x, y), координатные оси – Ox, Oy, базисные векторы – i , j , направленные отрезки на осях – OE₁, OE₂ . Векторы i, j называются базисными ортами.

Пусть произвольный вектор в декартовой СК имеет координаты (x, y), т.е. = xi + yj . Домножим это равенство скалярно на вектор i:

· i = x(i·i) + y(j·j) =x·1 + y· 0 = x.

А, с другой стороны,

· i =½½½i½ cosÐ(,i) =½½ cosÐ(i, ) = P_Ox.

Значит, x = P_Ox . Аналогично получаем y = P_Oy. Таким образом, в декартовой СК координаты вектора совпадают с его скалярными проекциями на координатные оси.

Пусть a =Ð( i, ), b =Ð( j, ). Тогда величины cos a и cos b называются направляющими косинусами вектора .

Пусть в произвольной аффинной СК, которая задаётся репером R = {O, , } известны координаты двух векторов: (x₁, x₂), (y₁, y₂). Тогда

+ = (x₁ + x₂ ) + (y₁ + y₂ ) = (x₁+y₁) + (x₂+y₂).

l = l(x₁ + x₂ ) = (lx₁) + (lx₂).

Значит, вектор + имеет координаты (x₁+ y₁, x₂ + y₂), а вектор l имеет координаты (lx₁,lx₂). Таким образом, при сложении векторов их координаты складываются, а при умножении вектора на число его координаты умножаются на это число. Также легко убедиться, что при вычитании векторов их координаты вычитаются.

Допустим, нам известны координаты двух точек P(x₁, x₂), Q(y₁, y₂), а = . Выясним, как найти координаты этого вектора.

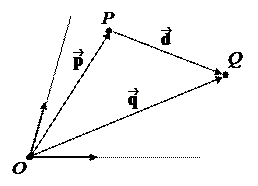Пусть = , = . Согласно определению, координаты точки совпадают с координатами ее радиус-вектора. Значит, (x₁, x₂), (y₁, y₂). По правилу тре-угольника + = , т.е. = – .

Значит, (y₁– x₁, y₂ – x₂).

Таким образом, для того, чтобы найти координаты вектора надо от координат его конца вычесть координаты начала.