Непрерывные системы случайных величин.
Так же как и раньше мы определим двумерную непрерывную случайную величину  как такую случайную величину, функция распределения которой
как такую случайную величину, функция распределения которой  непрерывна.
непрерывна.
С помощью функции  можно найти вероятность любого события вида
можно найти вероятность любого события вида
 , (6)
, (6)
т.е. вероятность попадания точки с координатами  в прямоугольник Q вида
в прямоугольник Q вида
 (Рис.1)
(Рис.1)
 |
Для этого применим к событиям  и
и  формулу сложения вероятностей:
формулу сложения вероятностей:
 Если теперь учесть, что события
Если теперь учесть, что события  и (6) несовместны и в сумме составляют событие
и (6) несовместны и в сумме составляют событие  , то будем иметь:
, то будем иметь:
 что и решает поставленную задачу.
что и решает поставленную задачу.
Перечислим ряд свойств функции  .Их доказательство проводится так же, как и в случае одной случайной величины
.Их доказательство проводится так же, как и в случае одной случайной величины  .
.
1. F(x2,y2)+F(x1,y1)-F(x1,y2)-F(x2,y1)≥0, если х1≤х2, у1≤у2 это следует из (7)
2. F(x, y) является неубывающей функцией по каждому из аргументов.
3. F(x, y) непрерывна слева по каждому из аргументов.
4. F(x, y) удовлетворяет соотношениям:
F (+∞, +∞ ) =  F(х, y ) =1,
F(х, y ) =1,

Свойства 1-4, как можно показать, являются характеристическими свойствами функции распределения. Это значит, что любая функция F(х, у), удовлетворяющая свойствам 1-4, является двумерной функцией распределения для некоторой системы случайных величин (ξ ,η).
Рассмотрим наиболее важный класс систем (ξ,η) с непрерывным распределением, для которых существует плотность вероятности.
Определение.Двумерная случайная величина (ξ,η) с функцией распределения F(x,y) имеет плотность вероятности, если существует неотрицательная функция
p(x, y) такая, что
F(x, y) =  . (8)
. (8)
Функция p(х,у)называется двумерной плотностью распределения (или плотностью вероятности) системы (ξ, η).
Из определения плотности p(x, y) следуют её свойства.
p(х,y)≥0,  . (9)
. (9)
Функция p(х,у), удовлетворяющая (9), может быть плотностью некоторого распределения с функцией распределения, заданной формулой (8).
Из формулы (8) следует, что
p(х,у)=  . (10)
. (10)
Заметим, что в случае непрерывного распределения, вероятность события ( (ξ,η) 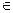 Г), где Г-кривая на плоскости, равна нулю.
Г), где Г-кривая на плоскости, равна нулю.
Из определения  также следует, что
также следует, что
Fξ(x)= 
 .
.
В случае существования плотности формула (7) преобретает наглядный вид:
P(x1≤ξ≤x2, y1≤η≤y2)=  , (11)
, (11)
где Q- прямоугольник (см. рис.1).
Из формулы сложения вероятностей и определения двойного интеграла, отсюда следует, что вероятность попадания точки с координатами (ξ,η) в заданную (измеримую) область произвольной формы G будет равна
P((  )
) 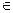 G)=
G)=  . (12)
. (12)
Примером многомерной плотности служит плотность p(x,y) равномерного распределения на области G конечной площади μ(G)в плоскости, задаваемая равенством
p(x,y)= 
Если В какая то область на плоскости, то вероятность
P((ξ,η) 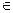 B)) в этом случае определяется отношением площадей B∩G и G:
B)) в этом случае определяется отношением площадей B∩G и G:
 . (13)
. (13)
По этой формуле вычисляются, так называемые, геометрические вероятности (см. §7 гл.1).
