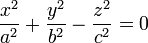Расстояние от точкидо плоскостивыражается формулой
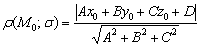
Билет №2(2)
Поверхность называется цилиндрической, если она образована параллельным перемещением некоторой прямой, называемой образующей, вдоль некоторой кривой, называемой направляющей. Тело, ограниченное цилиндрической поверхностью, называют бесконечным цилиндром.
Теорема. Если уравнение 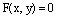 является уравнением кривой на координатной плоскости Оху, то это же уравнение является уравнением цилиндрической поверхности, направляющей которой служит данная кривая, а образующей является прямая, проходящая через точку данной кривой и параллельной оси Оz.
является уравнением кривой на координатной плоскости Оху, то это же уравнение является уравнением цилиндрической поверхности, направляющей которой служит данная кривая, а образующей является прямая, проходящая через точку данной кривой и параллельной оси Оz.
Цилиндрическойповерхностью называется поверхность, которая в некоторой декартовой системе координат определяется уравнением, в котором не фигурирует одна из переменных:
| F(x, y) = 0, F(x, z) = 0 или F(y, z) = 0 | |
| Если некоторая точка M0(x0, y0, z0) принадлежит цилиндрической поверхности, описываемой уравнением F(x, y) = 0 , то все точкипрямой, проходящей через эту точку параллельно оси OZ , также принадлежат цилиндрической поверхности. Такие прямые называются образующими цилиндрической поверхности, а кривая, описываемая уравнением F(x, y) = 0 и получающаяся в сечении любой плоскостью z = h , называется направляющей. | |
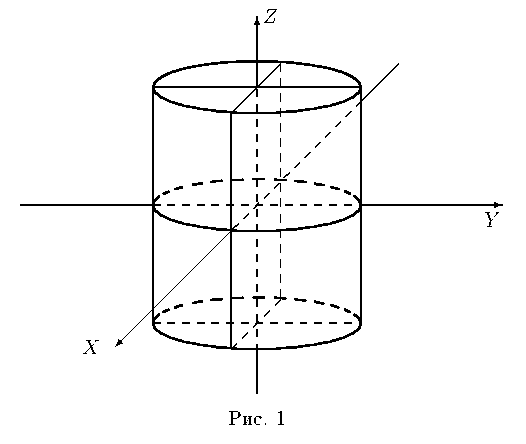 Эллиптический цилиндр.Уравнение Эллиптический цилиндр.Уравнение 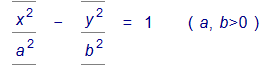 в трехмерном пространстве определяет цилиндрическую поверхность с образующими, параллельными оси OZ , направляющей является эллипсс полуосями a и b (рис. 1). в трехмерном пространстве определяет цилиндрическую поверхность с образующими, параллельными оси OZ , направляющей является эллипсс полуосями a и b (рис. 1). 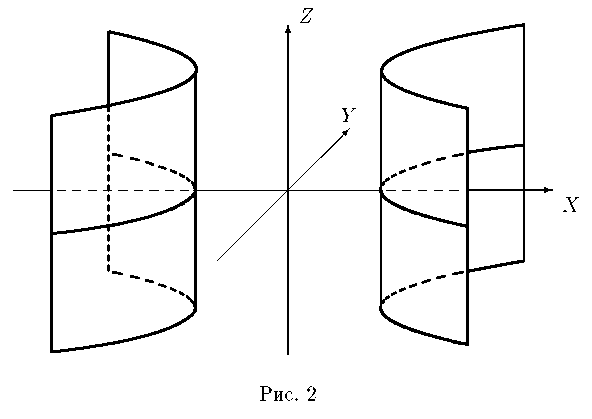 В частности, уравнение x2 + y2 = R2 в трехмерном пространстве определяет круглый цилиндр. Гиперболический цилиндр. Уравнение В частности, уравнение x2 + y2 = R2 в трехмерном пространстве определяет круглый цилиндр. Гиперболический цилиндр. Уравнение 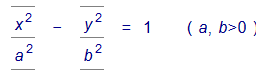 в трехмерном пространстве определяет цилиндрическую поверхность с образующими, параллельными оси OZ , направляющей является гиперболас полуосями a и b (рис. 2). в трехмерном пространстве определяет цилиндрическую поверхность с образующими, параллельными оси OZ , направляющей является гиперболас полуосями a и b (рис. 2). 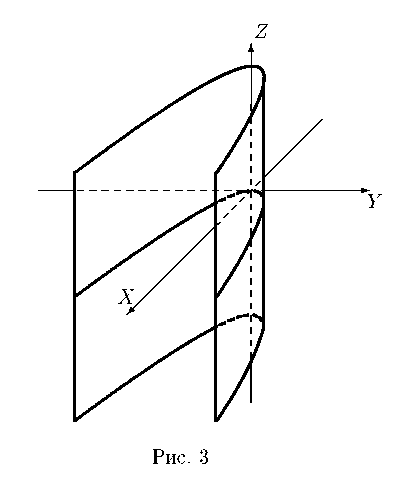 Параболический цилиндр. Уравнение Параболический цилиндр. Уравнение
в трехмерном пространстве определяет цилиндрическую поверхность с образующими, параллельными оси OZ , направляющей является парабола (рис. 3).
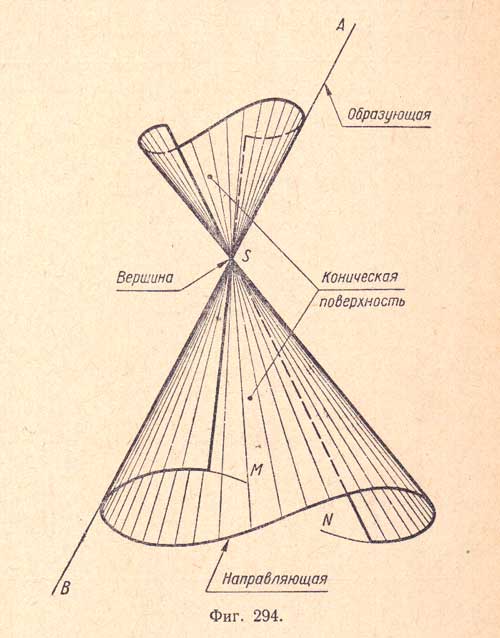
Конической поверхностью называется поверхность, образуемая движением прямой (AВ), перемещающейся в пространстве так, что она при этом постоянно проходит через неподвижную точку S и пересекает данную линию MN (фиг.294). Прямая АВ называется образующей, линия MN - направляющей, а точка S- вершиной конической поверхности. Каноническое уравнение круговой конической поверхности в декартовых координатах: Под действительным конусом второго порядка понимается поверхность второго порядка, которая задается этим уравнение:
|
Теорема:Если в некоторой декартовой прямоугольной системе координат поверхность 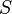 задана уравнением
задана уравнением 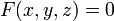 , где
, где 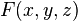 — однородная функция, то
— однородная функция, то 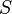 — коническая поверхность с вершиной в начале координат.
— коническая поверхность с вершиной в начале координат.
Если поверхность 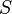 задана функцией
задана функцией 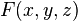 , являющейся однородным алгебраическим многочленом второго порядка, то
, являющейся однородным алгебраическим многочленом второго порядка, то  называется конической поверхностью второго порядка.
называется конической поверхностью второго порядка.
Билет №4(1)
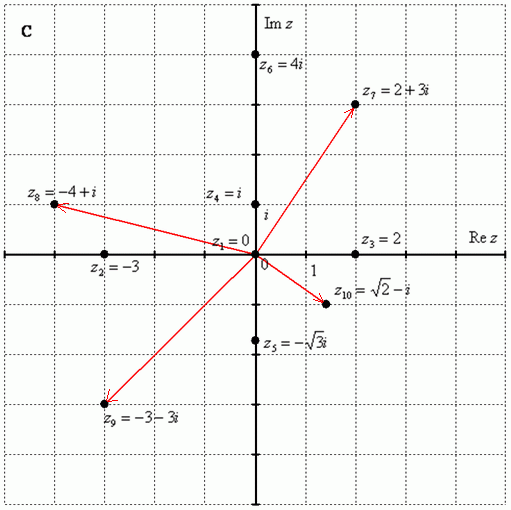 Ко́мпле́ксные чи́сла (устар. мнимые числа) — числа вида
Ко́мпле́ксные чи́сла (устар. мнимые числа) — числа вида 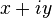 , где
, где 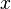 и
и 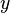 — вещественные числа,
— вещественные числа, 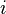 — мнимая единица; то есть
— мнимая единица; то есть 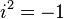 .
. 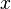 - действительная часть комплексного числа.
- действительная часть комплексного числа. 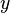 - мнимая часть комплексного числа.
- мнимая часть комплексного числа.
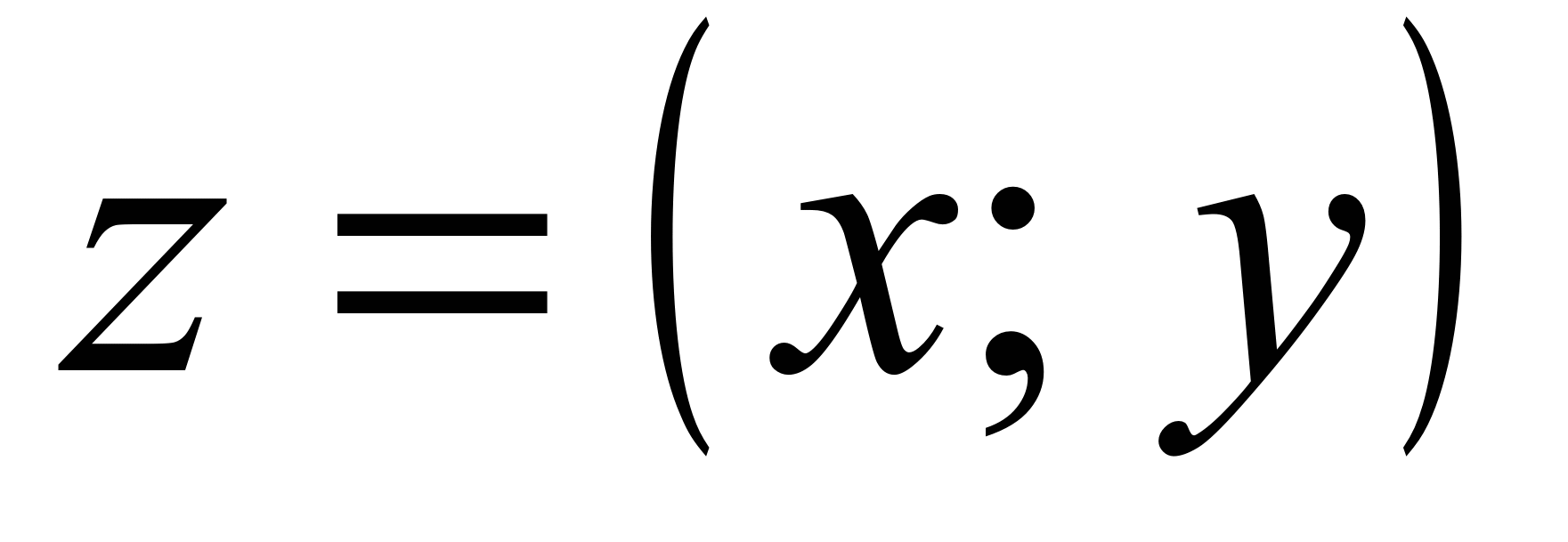
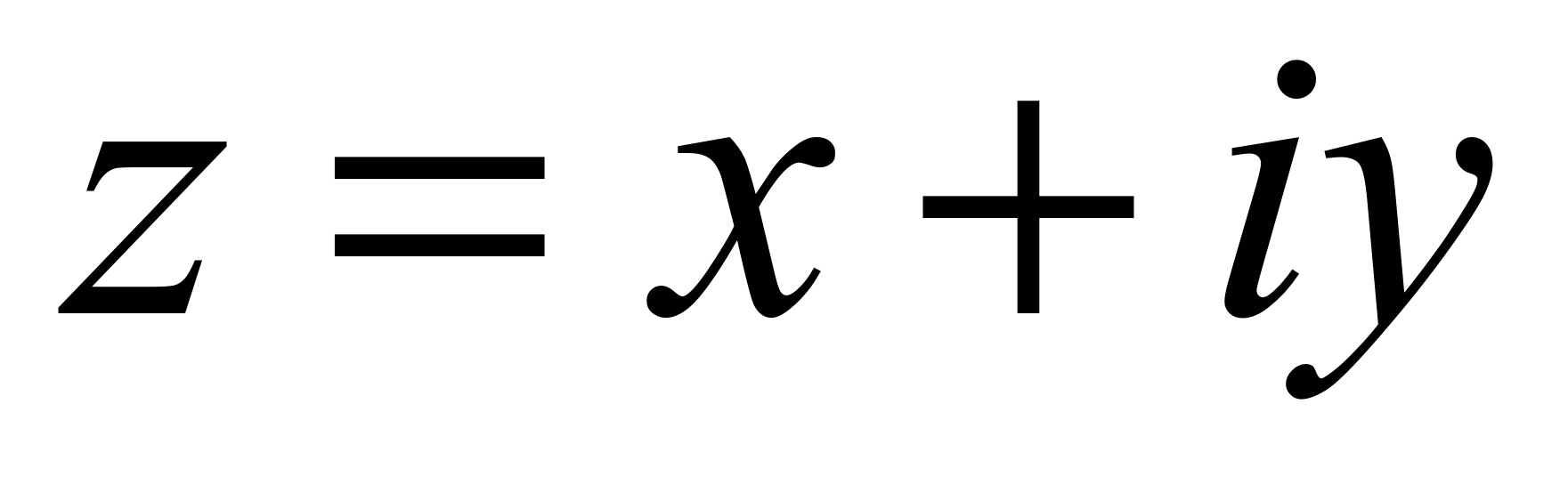 - Алгебраическая форма записи.
- Алгебраическая форма записи.
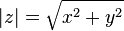
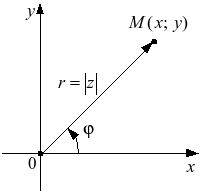
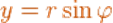
 Угол
Угол  между действительной осью
между действительной осью 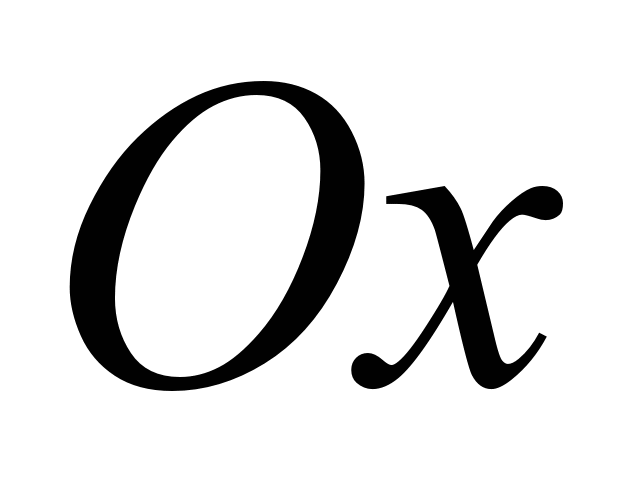 и вектором
и вектором 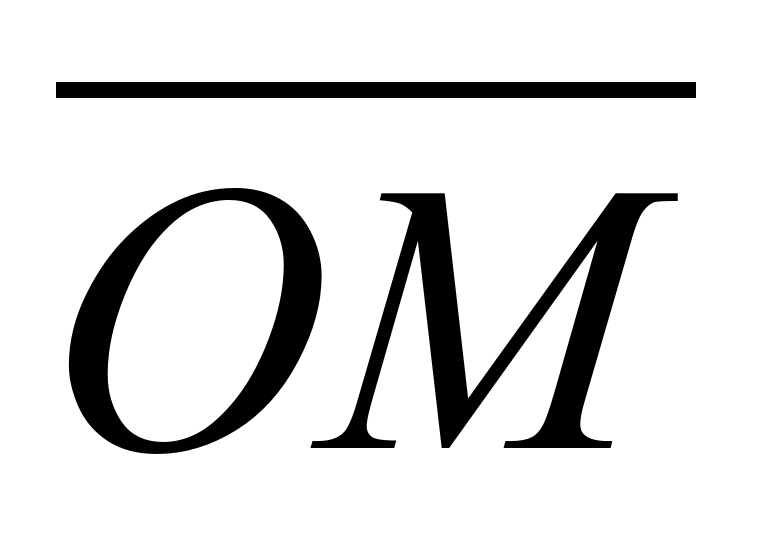 называется аргументом комплексного числа
называется аргументом комплексного числа  :
: 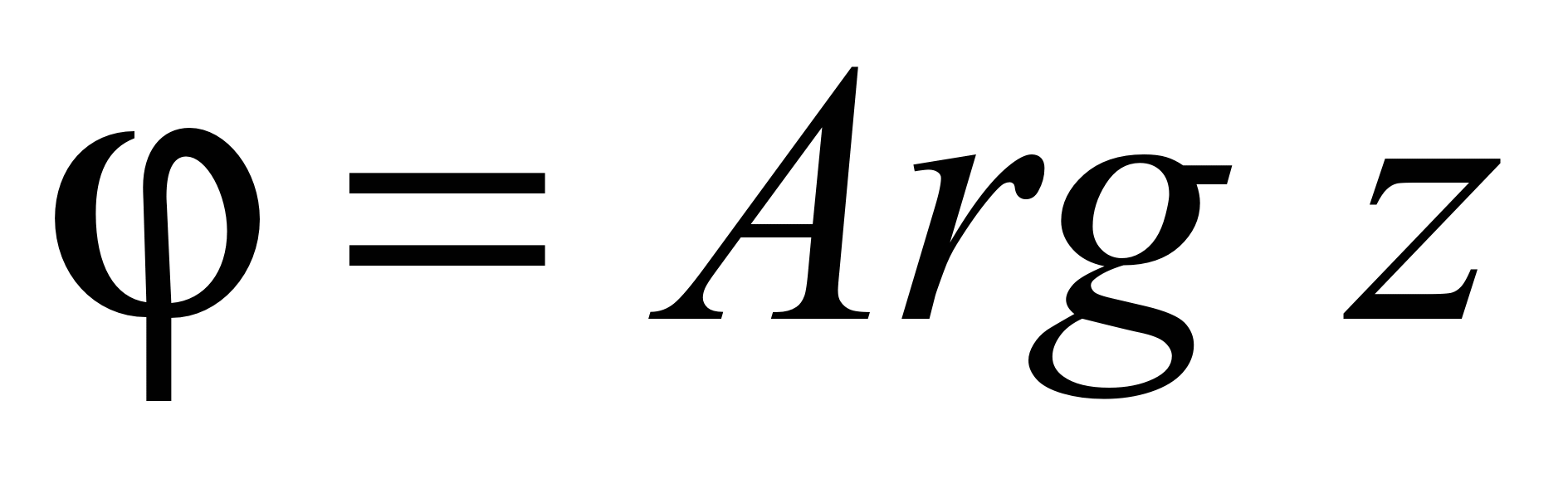 . Значение
. Значение  , заключенное в промежутке
, заключенное в промежутке 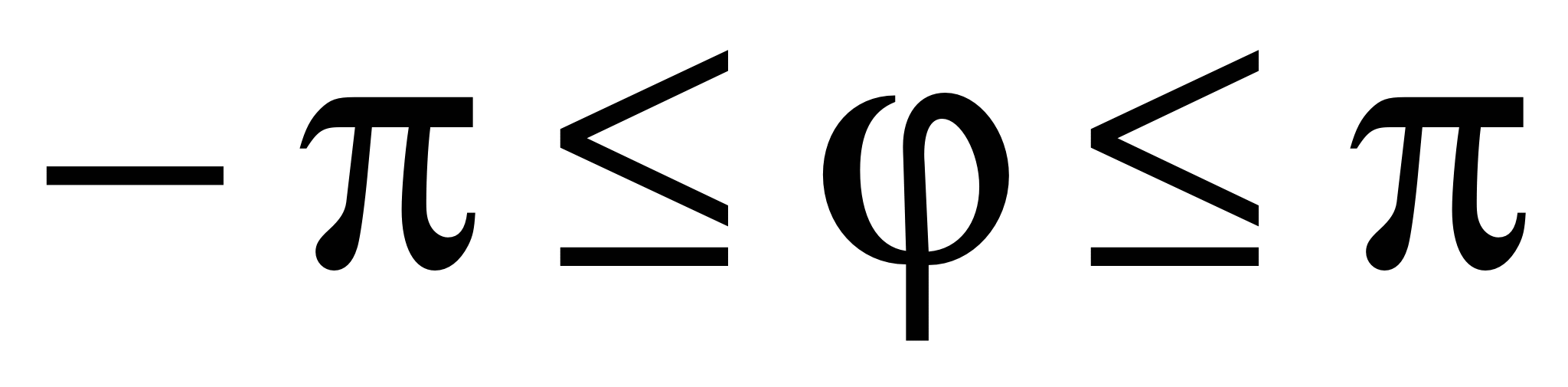 ,
,
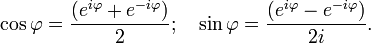

 - Тригонометрическая форма записи ,
- Тригонометрическая форма записи ,
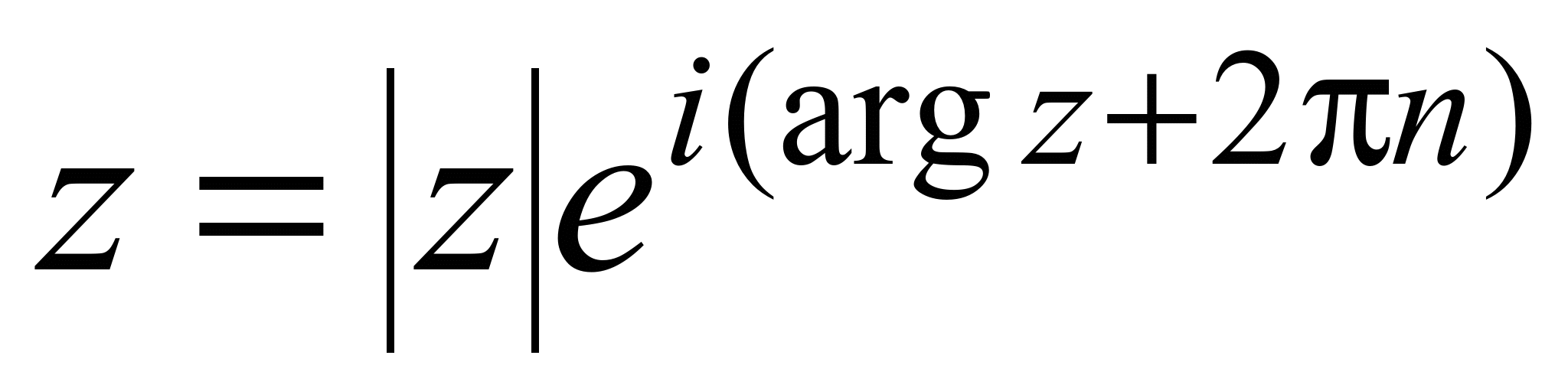 - Показательная форма записи.
- Показательная форма записи.
1) два комплексных числа z1 = (x1, y1) и z2 = (x2, y2) называются равными, если x1 = x2 и y1 = y2;
2) суммой комплексных чисел z1 и z2 называется комплексное число z вида
z = (x1 + x2, y1 + y2);
3) произведением комплексных чисел z1 и z2 называется комплексное число
z = (x1x2 - y1y2, x1y2 + x2y1);
4) множество комплексных чисел 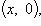
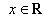 , отождествляется с множеством действительных чисел R.
, отождествляется с множеством действительных чисел R.
Сравнение
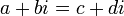 означает, что
означает, что  и
и 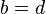 (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
(два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
Сложение
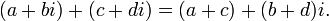
 Вычитание
Вычитание
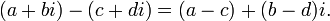
Умножение
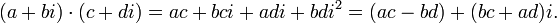
Деление
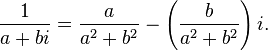
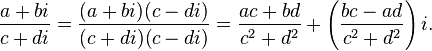
 Если комплексное число
Если комплексное число 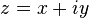 , то число
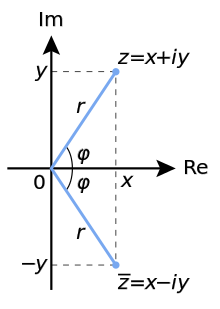
, то число 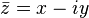 называется сопряжённым.На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.
называется сопряжённым.На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.

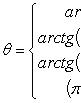
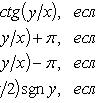
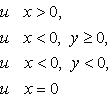
Формула Муавра для комплексных чисел 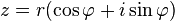 утверждает, что … для любого
утверждает, что … для любого 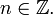
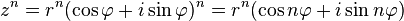
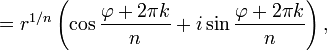
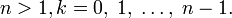
Билет № 7(2)«Множество есть совокупность различных элементов, мыслимая как единое целое»
Объекты, из которых состоит множество, называют элементами множества или точками множества. Множества чаще всего обозначают заглавными буквами латинского алфавита, его элементы — строчными. Если а — элемент множества А, то записывают а ∈ А(а принадлежит А). Если а не является элементом множества А, то записывают а ∉ А (а не принадлежит А).
Множество 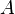 является подмножеством множества
является подмножеством множества 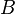 , если любой элемент, принадлежащий
, если любой элемент, принадлежащий 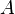 , также принадлежит
, также принадлежит 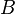 . Формальное определение:
. Формальное определение:
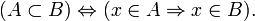
Пусто́е мно́жество— множество, не содержащее ни одного элемента. Ø Оно является подмножеством любого множества.
Числовые множества: (отрезок 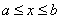 [a; b], полуотрезок[a; b),промежуток(a, b), числовой луч [a; +∞)).
[a; b], полуотрезок[a; b),промежуток(a, b), числовой луч [a; +∞)).
· множество всех натуральных чисел ( 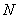 );
);
· множество всех положительных рациональных чисел ( 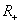 );
);
· множество всех рациональных чисел( 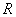 );
);
· множество всех целых чисел (  );
);
· множество всех чисел, удовлетворяющих неравенству 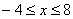 ;
;
· множество всех чисел вида 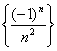 , где n принимает все натуральные значения.
, где n принимает все натуральные значения.
С каждым уравнением связаны два числовых множества. Первое из них – область определения уравнения. Второе - это множество его корней, т.е. чисел, при подстановке которых в уравнение оно обращается в тождество.
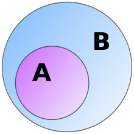
Пересечением множеств А и В называют новое множество Х, содержащее те и только те элементы, которые входят и в множество А и в множество В. Пересечение множеств А и В обозначают 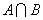 или AB
или AB
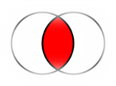
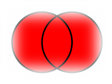
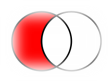

Объединением называют множество Х, состоящее из тех и только тех элементов, которые входят хотя бы в одно из этих множеств. Объединение двух множеств А и В обозначают 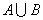 .
.
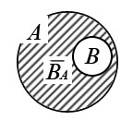
Разностью двух множествАиВ называют такое множество 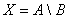 , в которое входят все элементы из А, не принадлежащие множеству В. При этом не предполагается, что множество В является частью множества А.
, в которое входят все элементы из А, не принадлежащие множеству В. При этом не предполагается, что множество В является частью множества А.
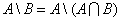
В случае, когда В – часть множества А, 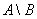 называют дополнением кВв множествеАи обозначают
называют дополнением кВв множествеАи обозначают 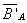 . Симметрическая разность двух множеств — теоретико-множественная операция, результатом которой является новое множество, включающее все элементы исходных множеств, не принадлежащие одновременно обоим исходным множествам.
. Симметрическая разность двух множеств — теоретико-множественная операция, результатом которой является новое множество, включающее все элементы исходных множеств, не принадлежащие одновременно обоим исходным множествам. 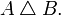
Билет №5(1)
Элементарная комбинаторика имеет дело с множествами, из которых выбираются подмножества с определенными свойствами.
Набор элементов x 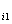 , …, x
, …, x 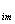 из множества Х = { x
из множества Х = { x 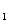 , …, x
, …, x 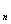 } называется выборкой объема m из n элементов.
} называется выборкой объема m из n элементов.
Выборки называются упорядоченными, если порядок следования элементов в них задан. Две упорядоченные выборки, различающиеся лишь порядком следования элементов, считаются различными.
Например, упорядоченные выборки ( x1, x5 ) и ( x5, x1 ) различные выборки объемом 2.
Если порядок следования элементов в выборке не является существенным, то такие выборки называются неупорядоченными
· Размещением без повторений из m элементов называется упорядоченная выборка объемом m, в которой элементы различны.
Число всех размещений без повторений объемом m , составленных из n различных элементов, обозначается через А 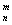 и вычисляется по формуле
и вычисляется по формуле
А 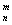 = n·(n-1)· … ·(n - m + 1) =
= n·(n-1)· … ·(n - m + 1) = 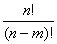
· Размещением с повторениями из m элементов называется упорядоченная выборка объемом m в которой элементы могут повторяться.
Число всех размещений с повторениями объемом m, составленных из nразличных элементов, обозначается через 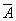
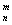 и вычисляется по формуле
и вычисляется по формуле
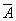
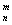 = n
= n 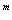 .
.
· Перестановкой из n элементов называется размещение без повторений объемом n.
Число всех перестановок из n элементов обозначается через Р 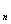 и вычисляется по формуле
и вычисляется по формуле
Р 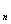 = n! = n·( n-1 )· … ·2·1.
= n! = n·( n-1 )· … ·2·1.
· Сочетанием без повторений из m элементов называется неупорядоченная выборка объемом m, в которой элементы различны.
Число всех различных сочетаний без повторений объемом m, которые могут быть составлены из n различных элементов обозначается через С 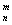 и вычисляется по формуле
и вычисляется по формуле
С 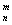 =
= 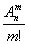 =
= 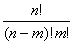
Граф — это совокупность непустого множества вершин и наборов пар вершин (связей между вершинами). Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра.
Билет №6(1)
Эллипсом называется геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух заданных точек 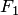 , и
, и 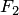 есть величина постоянная
есть величина постоянная 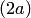 , бо́льшая расстояния
, бо́льшая расстояния 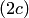 между этими заданными точками Это геометрическое определение выражает фокальное свойство эллипса.
между этими заданными точками Это геометрическое определение выражает фокальное свойство эллипса.
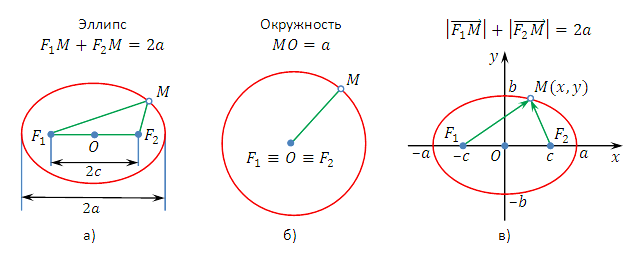
Точки  , и
, и 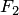 называются фокусами эллипса, расстояние между ними
называются фокусами эллипса, расстояние между ними 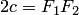 — фокусным расстоянием, середина
— фокусным расстоянием, середина 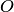 отрезка
отрезка 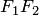 — центром эллипса, число
— центром эллипса, число 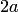 — длиной большой оси эллипса (соответственно, число
— длиной большой оси эллипса (соответственно, число  — большой полуосью эллипса). Отрезки
— большой полуосью эллипса). Отрезки 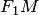 и
и 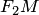 , соединяющие произвольную точку
, соединяющие произвольную точку 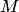 эллипса с его фокусами, называются фокальными радиусами точки
эллипса с его фокусами, называются фокальными радиусами точки 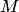 . Отрезок, соединяющий две точки эллипса, называется хордой эллипса.
. Отрезок, соединяющий две точки эллипса, называется хордой эллипса.
Отношение 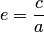 называется эксцентриситетом эллипса. Из определения
называется эксцентриситетом эллипса. Из определения 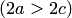 следует, что
следует, что 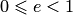 . При
. При 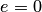 , т.е. при
, т.е. при 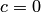 , фокусы
, фокусы 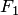 и
и 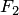 , а также центр
, а также центр 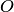 совпадают, и эллипс является окружностью радиуса
совпадают, и эллипс является окружностью радиуса  .
.
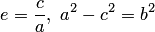 Каноническое уравнение эллипса:
Каноническое уравнение эллипса: 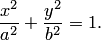
Директрисами эллипса называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии 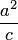 от нее. При
от нее. При 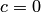 , когда эллипс является окружностью, директрис нет (можно считать, что директрисы бесконечно удалены).
, когда эллипс является окружностью, директрис нет (можно считать, что директрисы бесконечно удалены).
Эллипс с эксцентриситетом 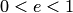 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки
можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки 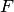 (фокуса) к расстоянию до заданной прямой
(фокуса) к расстоянию до заданной прямой 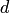 (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету
(директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету  (директориальное свойство эллипса). Здесь
(директориальное свойство эллипса). Здесь 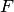 и
и 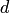 — один из фокусов эллипса и одна из его директрис, расположенные по одну сторону от оси ординат канонической системы координат, т.е.
— один из фокусов эллипса и одна из его директрис, расположенные по одну сторону от оси ординат канонической системы координат, т.е. 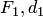 или
или 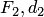 .
.
В самом деле, например, для фокуса 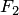 и директрисы
и директрисы 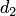 (рис.3.37,6) условие
(рис.3.37,6) условие 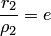 можно записать в координатной форме:
можно записать в координатной форме:
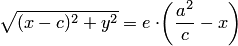
Уравнение эллипса в полярной системе координат 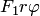 (рис.3.37,в и 3.37(2)) имеет вид
(рис.3.37,в и 3.37(2)) имеет вид
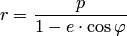 где
где 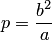 фокальный параметр эллипса.
фокальный параметр эллипса.
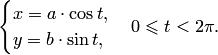 Параметрическое уравнение эллипса в канонической системе координат имеет вид
Параметрическое уравнение эллипса в канонической системе координат имеет вид
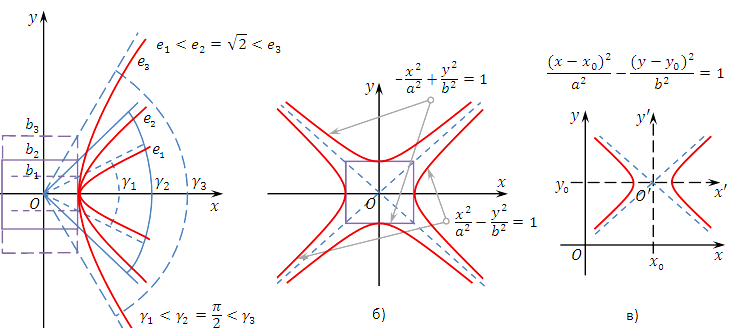
Гиперболойназывается геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек 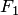 и
и 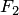 есть величина постоянная
есть величина постоянная 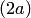 , меньшая расстояния
, меньшая расстояния 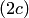 между этими заданными точками (рис.3.40,а). Это геометрическое определение выражает фокальное свойство гиперболы.
между этими заданными точками (рис.3.40,а). Это геометрическое определение выражает фокальное свойство гиперболы.
Точки 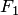 и
и 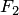 называются фокусами гиперболы, расстояние
называются фокусами гиперболы, расстояние 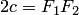 между ними — фокусным расстоянием, середина
между ними — фокусным расстоянием, середина  отрезка
отрезка 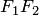 — центром гиперболы, число
— центром гиперболы, число 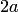 — длиной действительной оси гиперболы (соответственно,
— длиной действительной оси гиперболы (соответственно,  — действительной полуосью гиперболы). Отрезки
— действительной полуосью гиперболы). Отрезки 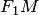 и
и 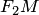 , соединяющие произвольную точку
, соединяющие произвольную точку 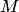 гиперболы с ее фокусами, называются фокальными радиусами точки
гиперболы с ее фокусами, называются фокальными радиусами точки 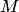 . Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.
. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.
Отношение 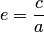 , где
, где 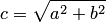 , называется эксцентриситетом гиперболы. Из определения
, называется эксцентриситетом гиперболы. Из определения 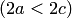 следует, что
следует, что 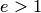 .
.
Геометрическое определение гиперболы, выражающее ее фокальное свойство, эквивалентно ее аналитическому определению — линии, задаваемой каноническим уравнением гиперболы:
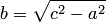
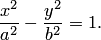
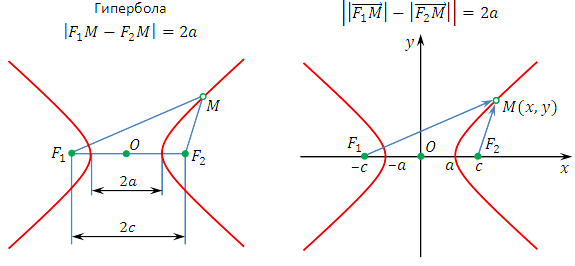
Составим уравнение гиперболы, используя геометрическое определение, выражающее фокальное свойство. В выбранной системе координат определяем координаты фокусов 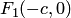 и
и 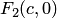 . Для произвольной точки
. Для произвольной точки 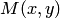 , принадлежащей гиперболе, имеем:
, принадлежащей гиперболе, имеем:
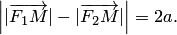
Записывая это уравнение в координатной форме, получаем:
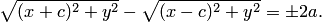
Директрисами гиперболы называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии 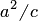 от нее. При
от нее. При 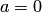 , когда гипербола вырождается в пару пересекающихся прямых, директрисы совпадают.
, когда гипербола вырождается в пару пересекающихся прямых, директрисы совпадают.
Гиперболу с эксцентриситетом 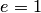 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки
можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки 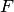 (фокуса) к расстоянию до заданной прямой
(фокуса) к расстоянию до заданной прямой 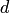 (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету
(директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету  (директориальное свойство гиперболы). Здесь
(директориальное свойство гиперболы). Здесь 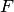 и
и 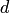 — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.
— один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.
В самом деле, например, для фокуса 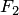 и директрисы
и директрисы 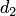 (рис.3.41,а) условие
(рис.3.41,а) условие 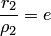 можно записать в координатной форме:
можно записать в координатной форме:
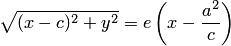
Избавляясь от иррациональности и заменяя 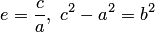 , приходим к каноническому уравнению гиперболы.
, приходим к каноническому уравнению гиперболы.
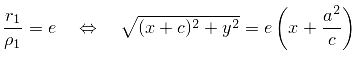
Уравнение правой ветви гиперболы в полярной системе координат  (рис.3.41,б) имеет вид
(рис.3.41,б) имеет вид
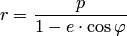 , где
, где 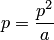 — фокальный параметр гиперболы.
— фокальный параметр гиперболы.
Параметрическое уравнение гиперболы в канонической системе координат имеет вид
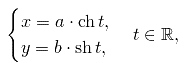
где 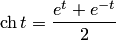 — гиперболический косинус, a
— гиперболический косинус, a 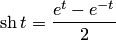 гиперболический синус.
гиперболический синус.
Билет №10(2)
Эллипсоидом называется поверхность, определяемая в некоторой прямоугольной системе координат  каноническим уравнением, и получена деформацией сферы вдоль трёх взаимно перпендикулярных осей.
каноническим уравнением, и получена деформацией сферы вдоль трёх взаимно перпендикулярных осей.
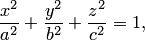
где 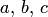 — положительные параметры, удовлетворяющие неравенствам
— положительные параметры, удовлетворяющие неравенствам 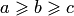
Эллипсоид, у которого две полуоси равны, называется эллипсоидом вращения (или сфероидом). Такой эллипсоид является поверхностью вращения. Например, если 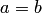 , то линии (4.47) при
, то линии (4.47) при 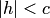 являются окружностями. Следовательно, сечения эллипсоида плоскостями
являются окружностями. Следовательно, сечения эллипсоида плоскостями 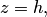
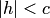 представляют собой окружности с центрами на оси аппликат. Такую поверхность можно получить, вращая вокруг оси
представляют собой окружности с центрами на оси аппликат. Такую поверхность можно получить, вращая вокруг оси 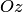 эллипс
эллипс 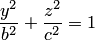 заданный в плоскости .
заданный в плоскости . 
· Если 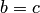 , то все сечения эллипсоида (4.46) плоскостями
, то все сечения эллипсоида (4.46) плоскостями 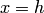 при
при 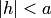 будут окружностями с центрами на оси абсцисс. Такой эллипсоид можно получить, вращая вокруг оси
будут окружностями с центрами на оси абсцисс. Такой эллипсоид можно получить, вращая вокруг оси 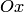 эллипс
эллипс 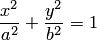
· Если все полуоси эллипсоида равны 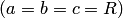 , то он представляет собой сферу
, то он представляет собой сферу 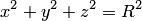 радиуса
радиуса 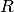 , которую можно получить, например, вращая окружность такого же радиуса вокруг любого диаметра.
, которую можно получить, например, вращая окружность такого же радиуса вокруг любого диаметра.
· Эллипсоид, у которого полуоси попарно различны 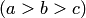 , называется трехосным (или общим).
, называется трехосным (или общим).
Эллипсоид обладает
- центральной симметрией относительно начала координат,
- осевой симметрией относительно координатных осей,
- плоскостной симметрией относительно начала координат.
Билет №11(2)
Параболо́ид ― тип поверхности второго порядка. Параболоид может быть охарактеризован как незамкнутая нецентральная (то есть не имеющая центра симметрии) поверхность второго порядка.
Канонические уравнения параболоида в декартовых координатах:
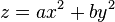
- если
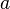 и
и 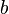 одного знака, то параболоид называется эллиптическим.
одного знака, то параболоид называется эллиптическим. - если
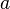 и
и 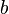 разного знака, то параболоид называется гиперболическим.
разного знака, то параболоид называется гиперболическим. - если один из коэффициентов равен нулю, то параболоид называется параболическим цилиндром.
Эллипти́ческий параболо́ид — поверхность, задаваемая функцией вида
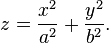
Эллиптический параболоид можно описать как семейство параллельных парабол с ветвями, направленными вверх, вершины которых описывают параболу, с ветвями, также направленными вверх.
Если 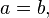 то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы вокруг её оси симметрии.
то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы вокруг её оси симметрии.
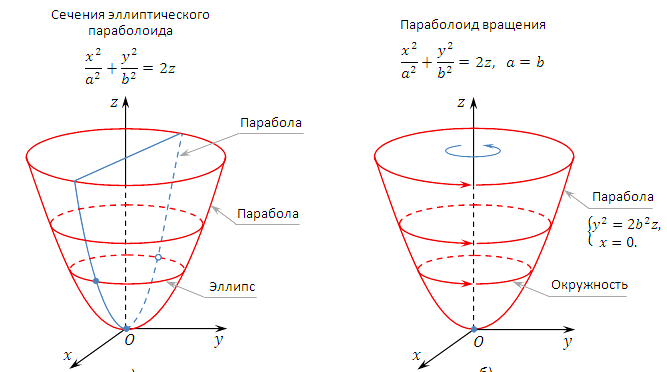
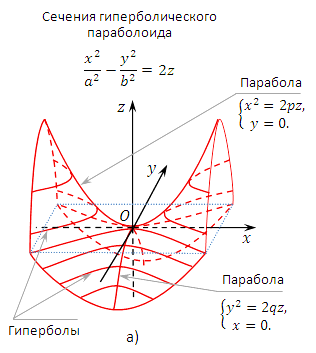
Плоскость 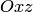 пересекает эллиптический параболоид по линии, имеющей в этой плоскости уравнение
пересекает эллиптический параболоид по линии, имеющей в этой плоскости уравнение 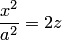 , которое равносильно уравнению
, которое равносильно уравнению 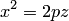 параболы с фокальным параметром
параболы с фокальным параметром 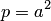 . Сечение параболоида плоскостью
. Сечение параболоида плоскостью 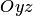 получаем, подставляя
получаем, подставляя 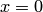 в уравнение:
в уравнение: 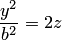 . Это уравнение равносильно уравнению
. Это уравнение равносильно уравнению 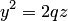 параболы с фокальным параметром
параболы с фокальным параметром 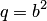 . Эти сечения называются главными параболами эллиптического параболоида
. Эти сечения называются главными параболами эллиптического параболоида
Гиперболи́ческий параболо́ид — седлообразная поверхность, описываемая в прямоугольной системе координат уравнением вида
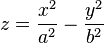 .
.
Также гиперболический параболоид может быть образован движением параболы, ветви которой направлены вниз, по параболе, ветви которой направлены вверх, при условии, что первая парабола соприкасается с вершиной второй. Гиперболический параболоид является линейчатой поверхностью.
Билет №7(1)
Окружностью называется фигура, состоящая из всех точек плоскости, находящихся от данной точки на данном расстоянии. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности.
Часть плоскости, ограниченная окружностью называется кругом.
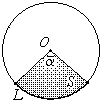
Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сегментомназывается часть круга, ограниченная дугой и стягивающей ее хордой.
Прямая, имеющая с только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
Свойства касательной
- Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
-
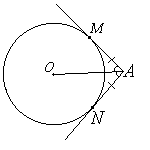
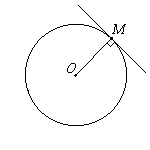 Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Отрезок, соединяющий две точки окружности, называется ее хордой.Хорда, проходящая через центр окружности, называется диаметром.
 Свойства хорд
Свойства хорд
- Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.
- Дуги, заключенные между параллельными хордами, равны.
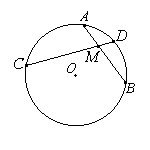
- Если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD.
Свойства окружности
· Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).
· 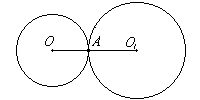 Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
· Точка касания двух окружностей лежит на линии, соединяющей их центры.
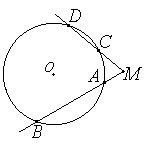
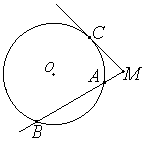 Теорема о касательной и секущей
Теорема о касательной и секущей
Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC^2 = MA•MB. 
Теорема о секущих
Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть. MA•MB = MC•MD.
Центральнымуглом в окружности называется плоский угол с вершиной в ее центре.
Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом.
Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугойокружности. Мерой дуги может служить мера соответствующего ей центрального угла.
Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
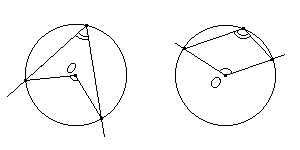
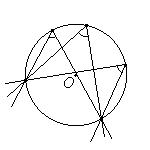
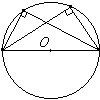
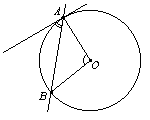
- Вписанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°.
- Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны.
- Вписанный угол, опирающийся на диаметр, равен 90°.
- Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.
- Длина окружности C радиуса R вычисляется по формуле:
 C = 2
C = 2 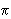 R.
R.
- Площадь S круга радиуса R вычисляется по формуле:
S = 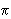 R2.
R2.
- Длина дуги окружности L радиуса R с центральным углом
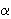 ,измеренным в радианах, вычисляется по формуле:
,измеренным в радианах, вычисляется по формуле:
L = R 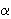 .
.
- Площадь Sсектора радиуса R с центральным углом в
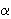 радиан вычисляется по формуле:
радиан вычисляется по формуле:
 S =
S = 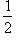 R2
R2 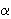 .
.
Окружность и треугольник
- центр вписанной окружности — точка пересечения биссектрис треугольника, ее радиус r вычисляется по формуле:
r = 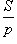 ,
,
где S — площадь треугольника, а 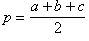 — полупериметр;
— полупериметр;
-
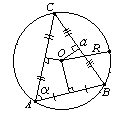 центр описанной окружности — точка пересечения серединных перпендикуляров, ее радиус Rвычисляется по формуле:
центр описанной окружности — точка пересечения серединных перпендикуляров, ее радиус Rвычисляется по формуле:
R = 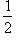
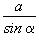 ,
,
R = 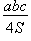 ;
;
здесь a, b, c — стороны треугольника, 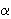 — угол, лежащий против стороны a, S — площадь треугольника;
— угол, лежащий против стороны a, S — площадь треугольника;

 Билет №3(2), Билет №4(2)
Билет №3(2), Билет №4(2)