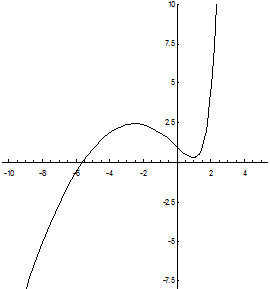Определение. Нахождение решения уравнения , удовлетворяющего начальным условиям , называется решением задачи Коши

Теорема Коши. (Теорема о необходимых и достаточных условиях существования решения задачи Коши).

Если функция (n-1) –й переменных вида 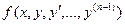в некоторой области D (n-1)- мерного пространства непрерывна и имеет непрерывные частные производные по 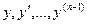, то какова бы не была точка ( ) в этой области, существует единственное решение уравнения , определенного в некотором интервале, содержащем точку х₀, удовлетворяющее начальным условиям .

Дифференциальные уравнения высших порядков, решение которых может быть найдено аналитически, можно разделить на несколько основных типов.

Рассмотрим подробнее методы нахождения решений этих уравнений.

Уравнения, допускающие понижение порядка.

Понижение порядка дифференциального уравнения – основной метод решения уравнений высших порядков. Этот метод дает возможность сравнительно легко находить решение, однако, он применим далеко не ко всем уравнениям. Рассмотрим случаи, когда возможно понижение порядка.

Уравнения вида y⁽ⁿ⁾ = f(x).

Если f(x) – функция непрерывная на некотором промежутке a < x < b, то решение может быть найдено последовательным интегрированием.

…………………………………………………………….

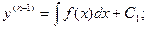
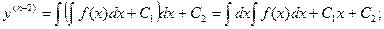
Пример. Решить уравнение 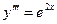с начальными условиями x₀ = 0; y₀ = 1;

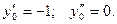
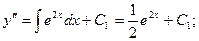
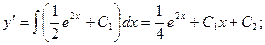
Подставим начальные условия:

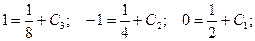
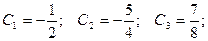
Получаем частное решение (решение задачи Коши): .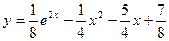

Ниже показана интегральная кривая данного дифференциального уравнения.