Сформулировать свойства пределов функций, имеющих конечные пределы. Рассказать о предельном переходе в неравенствах функций

Дать определение предела числовой последовательности; определения бесконеч-но малых (б.м.) и бесконечно больших (б.б.) числовых последовательностей. Рас-сказать о связи б.м. и б.б. числовых последовательностей.

Число а называется пределом числовой последовательности{x_n}, если для любого сколь угодного малого положительного числа £ существует номер n₀ такой, что все элементы последовательности с номерами n>n₀ удовлетворяющие неравенству |x_n - a|< £.

Число а называется пределом числовой последовательности {x_n}, тогда и только тогда, когда вне любой £-окрестности точки а находится лишь конечное число элементов этой последовательности

Если предел числовой последовательности конечный, то последовательность называется сходящейся. Если предел числовой последовательности бесконечный или не существует называется расходящейся.

Бесконечно малая числовая последовательность – это последовательность, предел которой равен нулю.

Х_n = 1/n, n = 1,2…. – является бесконечно малой.

Бесконечно большая последовательность — это последовательность, предел которой равен бесконечности.

{X_n} = ∞

Связь бесконечно малой и большой числовой последовательности.

Теорема без доказательства.

Если {X_n} – бесконечно большая последовательность, то {1/X_n} является бесконечно малой последовательностью ¹/_{бесконечность} → 0; Если {X_n} – бесконечно малая последовательность и все элементы последовательности отличны от 0, то последовательность {1/X_n} является бесконечно большой последовательностью ¹/_→0→∞.

Билет 14.

Доказать теорему о предельном переходе в неравенствах для числовых последовательностей.

Теорема о предельном переходе в неравенствах.

Пусть f(x) и g(x), x→R (множество действительных чисел) а – предельная точка множества Х. Пусть любой х ϵ Х; f(x) ≤ g(x). Пусть lim_x→a f(x) = A, lim_x→a g(x) = B тогда А≤В.

Доказательство.

Возьмем {X_n}, х ϵ Х, X_n ≠ а, X_n→а. По условию f(X_n)→A, g(X_n)→B. Любой n f(X_n)≤ g(X_n). Откуда по теореме о предельном переходе в неравенствах для последовательностей вытекает, что А≤В.

Билет 16.

Дать определения предела функции в точке и односторонних пределов в точке. Дать определение непрерывности функции в точке и вывести правило о предельном переходе под знаком непрерывной функции.

Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Односторонний предел в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом (или пределом слева) и правосторонним пределом (пределом справа).

Функция f(x), определенная в окрестности некоторой точки Х₀, называется непрерывной в точкеХ₀, если предел функции и ее значение в этой точке равны, т.е.

lim f(x) = f(X₀) 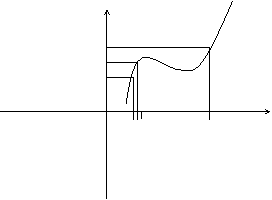Пример непрерывной функции.

Билет 18.

Сформулировать свойства пределов функций, имеющих конечные пределы. Рассказать о предельном переходе в неравенствах функций.

Предел функции — одно из основных понятий математического анализа. Функция f(x) имеет предел L в точке x₀, если для всех значений x, достаточно близких к x₀, значение f(x) близко к L.

1) Предел постоянной велечины равен самой постоянной величине.

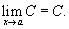
2) Предел суммы 2 функций равен сумме пределов этих функций.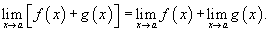

Аналогично предел разности 2 функций равен разности пределов этих функций.

3) Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела.

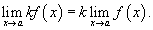
4) Предел произведения двух функций равен произведению пределов этих функций.

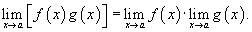
5) Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю.

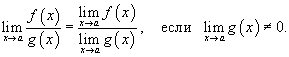
Теорема. Если элементы сходящейся последовательности {xn}, начиная с некоторого номера, удовлетворяют неравенству xn ≥ b (xn ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b).

Доказательство.

Пусть все элементы xn, по крайней мере начиная с некоторого номера, удовлетворяют неравенству xn ≥ b. Требуется доказать неравенство a ≥ b. Предположим, что a < b. Поскольку a - предел последовательности {xn}, то для положительного ε = b - a можно указать номер N такой, что при n ≥ N выполняется неравенство |xn - a| < b - a. Это неравенство эквивалентно следующим двум неравенствам: -(b - a) < xn - a < b - a. Используя правое из этих неравенств, получим xn < b, а это противоречит условию теоремы. Случай xn ≤ b рассматривается аналогично. Теорема доказана.

Билет 20.