Для решения системы (1) необязательно вычислять отдельно, а затем сравнивать ранги матриц А и . Достаточно сразу применить метод Гаусса

Заметим, что метод Гаусса по сравнению с другими:

· менее трудоёмкий;

· позволяет однозначно установить, совместна система или нет;

· в случае совместности позволяет найти её решения;

· позволяет найти максимальное число линейно независимых уравнений – ранг матрицы системы.

Пример.Решите систему методом Гаусса

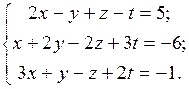
Решение. Для данной системы запишем соответствующую расширенную матрицу и с помощью элементарных преобразований

приведём её к ступенчатому виду:

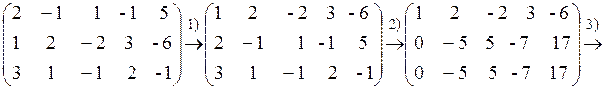
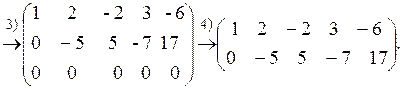
Мы применили следующие элементарные преобразования:

1) переставили местами 2-ю и 1-ю строки;

2) последовательно ко 2-й и 3-й строкам прибавили первую строку, умноженную соответственно на (- 2) и (- 3); тем самым в 1-м столбце получили все нули, кроме первого элемента;

3) из 3-й строки вычли 2-ю, получили нулевую строку;

4) удалили нулевую строку.

В результате расширенную матрицу размера 3 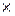5 привели к ступенчатому виду (матрице размера 2 5). Видим, что ранг r = r (А) =

= r ( 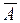) = 2, т.е. система совместна. Так как число неизвестных m = 4, r < m, то система имеет бесконечное множество решений.

Число уравнений системы n = 3; r < n, тогда две переменные (т.к. r = 2) х, у возьмём за основные. Определитель из коэффициентов при них (базисный минор) отличен от нуля:

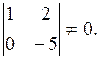
Остальные неосновные переменные z и t перенесём в правые части уравнений. Получим систему уравнений:

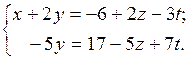
Из последнего уравнения имеем у = 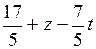. Подставив это выражение в первое уравнение, получим x = .

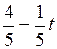Итак, система имеет бесконечное множество решений

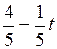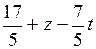( ; ; z; t), где z, t - любые числа.

Пример.Решите систему

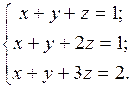
Решение. Для данной системы

А = 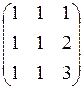- основная матрица; 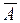= 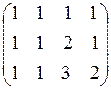- расширенная матрица. Ранг основной матрицы r (А) = 2, т.к. определитель det A = 0, но есть определители 2-го порядка, отличные от нуля, например,

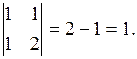
Ранг расширенной матрицы r ( 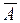) = 3. Так как r (А) ≠ r ( 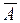), то система не имеет решений, т.е. несовместна.