Под множеством будем понимать любую совокупность определенных и различимых между собой объектов, рассматриваемую как единое целое.

Принадлежность некоторого элемента x множеству A обозначается как xÎA — «x есть элемент множества A» или «x принадлежит множеству A» . В свою очередь, непринадлежность некоторого элемента а множеству Мобозначается в виде: аÏ М или а 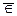М.

· Пустое множество. Пустым множеством называется множество, не содержащее ни одного элемента. Пустое множество обозначают символом Æ.

· Подмножество и надмножество. Множество Aназывается подмножеством множества B, если любой элемент, принадлежащий A, также принадлежит B. Это записывается в виде отношения включения: A Í B. Таким образом, (AÍB) Û (xÎA ® xÎB).Множество B, в свою очередь, называется надмножеством множества A, что записывается в виде отношения обратного включения: B Ê A.

Пустое множество является подмножеством любого множества.

· Универсальное множество. Обычно, в конкретных рассуждениях элементы всех множеств берутся из некоторого одного, достаточно широкого множества, своего для каждого случая, которое называется универсальным множеством (универсумом). Универсальное множество обычно обозначается U (от англ. universe, universal set), реже E.

· Мощность множества можно рассматривать как числовую характеристику (метрику) любого множества. Мощностью некоторого конечного множества А является число его элементов. Мощность множества А принято обозначать |А|, например, мощность множества А={a, b, c} равна |А|=3.

Мощность пустого множества равна нулю: |Æ|=0.

· Конечные и бесконечные множества. Множества, имеющие конечное число элементов и, соответственно, конечное значение мощности, называются конечными, а множества с бесконечным числом элементов и, соответственно, с бесконечной мощностью - бесконечными.

Множества, обладающие одинаковым значением мощности, называются равномощными. Понятие равномощности распространяется и на бесконечные множества.

· Счетные и несчетные множества. Бесконечные множестваразделяются на счётные и несчетные. Бесконечное множество называется счетным, если его элементы можно пронумеровать, в противном случае, бесконечное множество называется несчетным.

Простейшим примером счетного множества является множество всех натуральных чисел,

Простейшим примером счетного множества является множество всех натуральных чисел, в связи с чем можно дать другое определение счетного множества: множество называется счетным, если оно равномощно множеству натуральных чисел, т.е. его можно представить в виде {x₀, x₁, x₂, …}, где х_i – элемент множества, однозначно соответствующий его номеру (индексу) i.

В свою очередь, простейшим примером несчетного множества является множество действительных чисел.

Другими примерами счетных множеств являются множества целых и рациональных чисел, а примером несчетного множества – множество комплексных чисел.

· Булеан множества. Любое конечное множество содержит и конечное число подмножеств. Связь между произвольным множеством и всеми его подмножествами определяется булеаном.

Булеаноммножества А называется множество всех его подмножеств. Булеан множества А будем обозначать В(А).

Иначе булеан множества А называют множеством - степенью множества А.

Булеан как множество всех подмножеств множества А должен включать в себя:

- пустое множество;

- само множество А;

- отдельные элементы множества А;

- всевозможные комбинации различных элементов множества А.

Замечание. Если множество А содержит n элементов, то число его подмножеств из k элементов представляет собой число сочетаний из n по k и определяется по формуле:

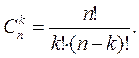
Пример 1.1.Записать булеан (множество – степень) для множества А={a,b, c}.

B(A)={Æ,{a},{b},{c},{a, b},{a, c},{b, c},{a, b, c}}.

Утверждение. Если множество А состоит из n элементов, то множество B(A) всех его подмножеств состоит из 2ⁿ элементов, т.е.

|А|= n ® |B(A)|=2ⁿ=2^|А|.

Способы задания множеств

Множества могут быть заданы списком, порождающей процедурой, описанием свойств элементов или графическим представлением.

1. Задание множеств списком предполагает перечисление элементов. Например, множество А состоит из букв a, b, c, d : A={a ,b, c, d}или множество L включает цифры 0, 2, 3, 4 : L={0, 2, 3, 4 }.

2. Задание множеств порождающей процедурой означает описание характеристических свойств элементов множества: X = { x | H (x) }, т. е. множество X содержит такие элементы x, которые обладают свойством H (x).

Например:

B = { b| b= p / 2 ± k p, k Î N }, N - множество всех натуральных чисел.

3. Задание множества описанием свойств элементов. Например, M- это множество чисел, являющихся степенями двойки.

К описанию свойств естественно предъявить требования точности и недвусмысленности

4. Графическое задание множеств осуществляют с помощью диаграмм Эйлера-Венна.

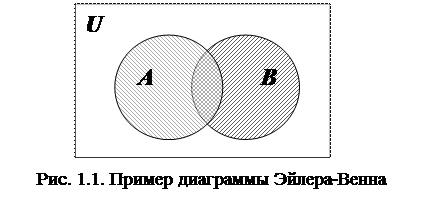
Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих рассматриваемые множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств

Леонард Эйлер (1707-1783) - швейцарский математик, механик, физик, астроном

Джон Венн (1834-1923) - английский математик и логик

На рис. 1.1 приведена диаграмма Эйлера-Венна, на которой показаны универсальное множество U и множества A и B.