Оценка погрешности формул прямоугольников и трапеций

Понятно, что приближенный результат следует использовать лишь тогда, когда известна его оценка.

Из теории приближенных методов вычислений известна оценка абсолютных погрешностей формул прямоугольников 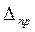и трапеций :

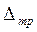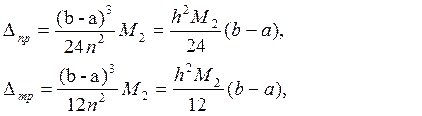(6)

где 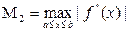, f(x) — подынтегральная функция, [a; b] —отрезок интегрирования, h – шаг интегрирования, ( 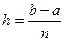). Таким образом, если на [a; b] можно найти М₂, то при заданном n (или h) по формулам (6) определяем абсолютную погрешность соответствующих приближенных результатов.

Из сравнения формул (1) - (3) и (5) и формул для их погрешностей (6) можно заключить, что они одинаково трудоемки и дают примерно одинаковой точности результат (погрешность порядка h²). Поэтому ни у одного из этих методов нет преимущества перед другим.

Замечание. Если функция f(х) задана таблично, то в формулах (6) f"(х) можно заменить на конечную разность 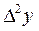. Так что

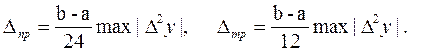
Формула Симпсона

Более точной, чем формула трапеций, является формула Симпсона. Для достижения той же точности в ней можно брать меньшее число n участков разбиения и соответственно больший шаг h, а при одном и том же шаге h, (т. е. при том же объеме вычислений), она дает меньшие абсолютную и относительную погрешности.

Формулу Симпсона можно получить следующим образом. Разобьем участок [а, b] на четное число частей n = 2m точками

а=x₀<x₁<...<x_n-1<x_n=b .

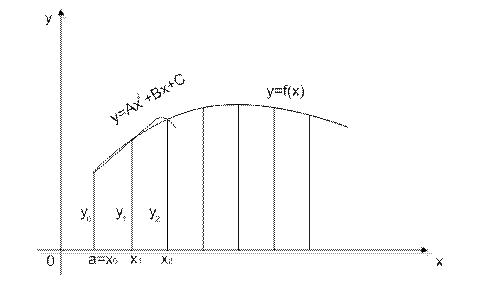
Рисунок 2.5 – Вывод формулы Симпсона

Обозначим ординаты в точках деления через y₀, y₁,...,y_n и рассмотрим пару соседних участков, например, с левым концом в точке а=х₀ (рис. 2.5). Проведем через три точки кривой с координатами (х₀, у₀), (x₁, у₁), (х₂, у₂) параболу с осью, параллельной оси Оу. Ее уравнение будет

у = Ах² + Вх + С (7)

Заменив площадь заданной криволинейной трапеции на участке [х₀, х₂] площадью криволинейной трапеции, ограниченной параболой (7), придем к приближенному равенству:

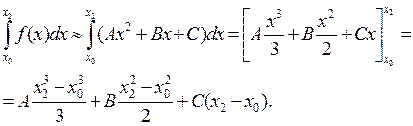
Вынося за скобку общий множитель 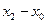и приводя к общему знаменателю, получим:

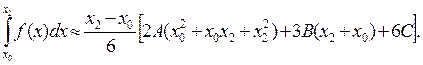(8)

Неизвестные коэффициенты А, В, С в формулах (7) и (8) находятся из условия, что при значениях х, равных х₀, х₁, х₂, функция f(x) принимает соответственно значения у₀, у₁, у₂. Заметив, что 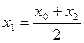, запишем эти условия в виде

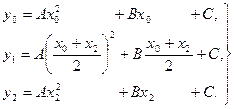(9)

Умножая второе равенство (9) на 4 и складывая после этого все три равенства (9), находим

у₀ + 4у₁ + у₂ = А[x₀² + (х₀ + х₂)² + x₂²] + В[х₀ + 2(х₀ + х₂) + х₂] + 6С =

= 2А (x₀² + х₀х₂ + x₂²) + 3B (х₀ + х₂) + 6С, (10)

что совпадает с квадратной скобкой в правой части равенства (8).

Подставив (10) в правую часть равенства (8) и заметив, что

x₂ – x₀=2h, где h = (b – a)/n, придем к приближенному равенству

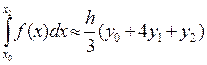. (11)

Ясно, что для каждой следующей пары участков получается такая же формула:

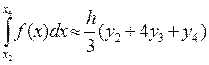(12)

Суммируя равенства вида (11) и (12) по всем участкам, получим формулу Симпсона:

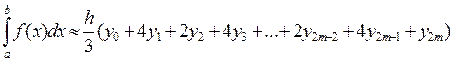(13)

Учитывая геометрический смысл формулы, ее называют также формулой парабол. В ней все ординаты с нечетными номерами умножаются на четыре, а все ординаты с четными номерами (кроме крайних) – на два. Крайние ординаты у₀ и у_2m входят в формулу с коэффициентами, равными единице.

Формула Гаусса

Предыдущие методы предусматривали интегрирование с произвольным разбиением интервала. Фактически разбиение производилось на равные отрезки. Метод Гаусса предусматривает ограниченное количество интервалов, причем концы интервалов располагаются так, чтобы получить наивысшую точность интегрирования (то есть уменьшить ошибку ограничения). Для этого пределы интегрирования заменяются так, чтобы они стали равными (+1;-1). Для этого вводится новая переменная 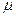так, что

,

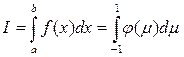где

.

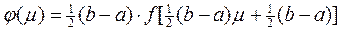Формула метода Гаусса для n ординат имеет вид:

,

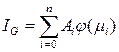где коэффициенты 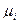, 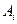определяются из таблиц, как функции количества ординат n.

В частности, для двух ординат формула Гаусса имеет вид:

,

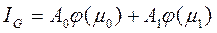Таблица значени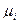й и 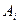для n = 2, 3, 4 приведена ниже.

Таблица 2 – Значения 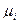и 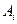для n = 2, 3, 4

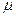n = 2	+0.5773502692 -0.5773502692	1.000
n = 3	+0.7745966692 -0.7745966692 0.00000000000	+0.5555555556 -0.5555555556 0.8888888889
n = 4	+0.8611363116 -0.8611363116 +0.3399810436 -0.3399810436	+0.3478548451 -0.3478548451 +0.6521451540 -0.6521451540