Методы прямоугольников и трапеций

Заменим исходную криволинейную трапецию ступенчатой фигурой, состоящей из n прямоугольников, опирающихся на частичные отрезки, причем высоты этих прямоугольников равны значениям функции 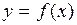в начальных или конечных точках частичных отрезков 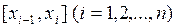(рис. 3.2). Значение площади этой фигуры и будет давать приближенное значение интеграла (3.1). Результат будет тем более точен, чем больше число частичных отрезков разбиения.

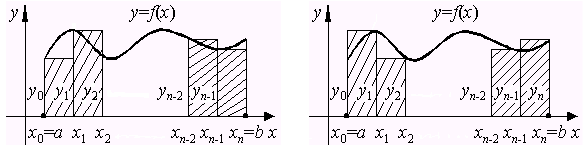
Рис. 3.2. Геометрическая иллюстрация методов левых и правых прямоугольников

Если обозначить значения функции 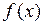в точках деления через 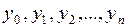, то, очевидно, будут иметь место следующие формулы:

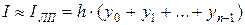, (3.2)

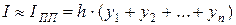, (3.3)

где в формуле (3.2) взяты значения функции в начальных точках, а в (3.3) в конечных точках частичных отрезков. Эти формулы называются формулами левых и правых прямоугольников. Из рис. 3.2 хорошо видно, что если брать значения функции в концах отрезков 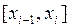, то приближение по площади будет или с избытком, или с недостатком на этих отрезках. Поэтому для повышения точности вычисления интеграла методом прямоугольников берут значения функции 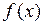в точках 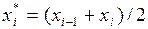, т. е. в серединах частичных отрезков (рис. 3.3).

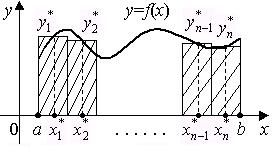
Рис. 3.3. Геометрическая иллюстрация метода средних прямоугольников

Тогда по формуле средних прямоугольников

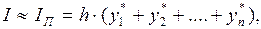(3.4)

где 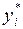– значения 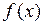в точках .

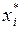Оставим разбиение отрезка 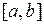прежним, но заменим теперь дугу линии 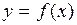, соответствующей частичному отрезку, хордой, соединяющей конечные точки этой дуги. Таким образом, заменяем данную криволинейную трапецию n прямолинейными (рис. 3.4).

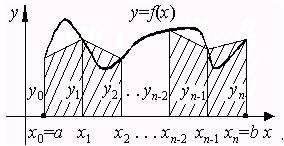
Рис. 3.4. Геометрическая иллюстрация метода трапеций

Как правило, площадь такой фигуры более точно выражает искомую площадь, чем площадь n-ступенчатой фигуры, составленной из прямоугольников. Из рис. 3.4 ясно, что площадь каждой прямолинейной трапеции, построенной на частичном отрезке, равна полусумме площадей, соответствующих этому интервалу левого и правого прямоугольников. Суммируя все эти площади, получим

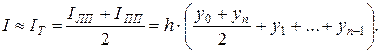(3.5)

Эта формула и носит название формулы трапеций.

Метод Симпсона

Как и раньше, разобьем 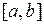на n равных частей, но предположим, что n – четное число: n=2m. Заменим дугу линии 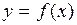, соответствующую отрезку 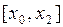, дугой параболы (поэтому метод и называют еще методом парабол), ось которой параллельна оси ординат и которая проходит через следующие три точки: начальную точку дуги 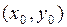, среднюю точку 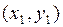и конечную 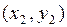(рис. 3.5).

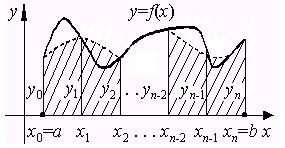
Рис. 3.5. Геометрическая иллюстрация метода Симпсона

Аналитически это означает, что в отрезке данная функция 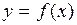заменяется квадратичной функцией

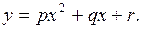(3.6)

Коэффициенты 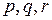выбираются так, чтобы значения обеих функций были равны при 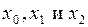соответственно:

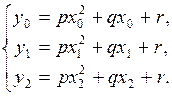(3.7)

Решая систему (3.7), находят коэффициенты 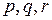. Проведя подобные замены во всех интервалах 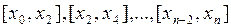(рис. 3.5), будем считать, что площадь исходной трапеции приближенно равна сумме площадей получившихся параболических трапеций, которые называются элементарными.

Покажем, что площадь S трапеции, ограниченной какой-нибудь параболой 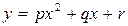с осью параллельной оси ординат будет выражаться формулой

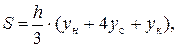(3.8)

где 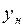– ордината начальной, 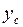– ордината средней и 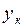– ордината конечной точек дуги параболы.

Предположим сначала, что основанием трапеции служит отрезок оси Ox, симметричный относительно начала координат, 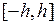(рис. 3.6).

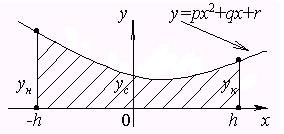
Рис. 3.6. Площадь параболической трапеции

Для площади такой параболической трапеции имеем выражение:

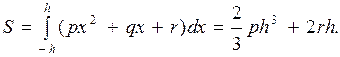
Так как здесь

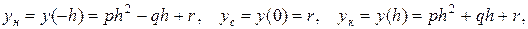
то непосредственной подстановкой этих значений в формулу (3.8) убеждаемся в ее справедливости. Эта формула справедлива для любой параболической трапеции рассматриваемого вида с основанием 2h, т. к. всегда можно выбрать декартову систему координат xOy, как показано на рис. 3.6, чтобы основание стало симметричным относительно начала координат. Тогда, применяя формулу (3.8) для всех элементарных параболических трапеций и суммируя площади этих трапеций, получим формулу Симпсона

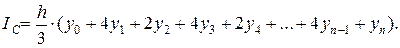(3.9)