Оценка погрешности квадратурных формул

Рассмотрим интеграл по элементарному отрезку

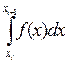
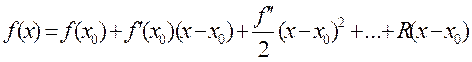
где х₀ Є [x_i,x_i+1]— некая опорная точка, тогда для приближенного значения интеграла верно

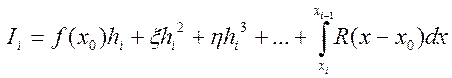
Коэффициенты ξ, η, ... зависят от производных f'(х₀), f''(х₀), ....

С другой стороны, любая из рассмотренных квадратурных формул представима в виде

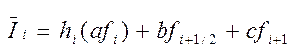
Заменяя в этой формуле значения функций f в точках f_i, f_{i + 1/2}, f_{i + 1} ее разложением по формуле Тейлора, получим

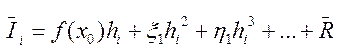
где х₀Є [x_i,x_i+1].

Сравнивая разложения для 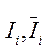, легко заметить, что вместе с первым слагаемым совпадают и другие слагаемые до (m - 1) - го порядка, так что ξ = ξ₁, η = η₁, ...

Разность же несовпадающих слагаемых будет, очевидно, оценкой погрешности квадратурной формулы на интервале

,

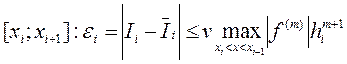где v — константа.

Если просуммировать локальные погрешности по всем интервалам [ x_i, x_{i + 1} ], то получим оценку погрешности квадратурной формулы по всему отрезку [a, b]:

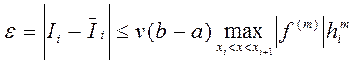
где h=(maxh_i)/i на неравномерной сетке, или h= (b - a)/n на равномерной. Число m называется порядком точности квадратуры.

Если подынтегральная функция имеет непрерывную вторую производную, то оценка погрешности:

Для формулы прямоугольников

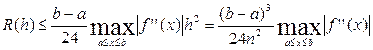
Для формулы трапеций

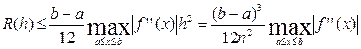
Если подынтегральная функция имеет непрерывную производную четвертого порядка, то справедлива такая погрешность формулы Симпсона:

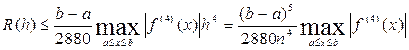
Заметим, что при интегрировании степенной функции, степень которой не выше трех, квадратурная формула Симпсона дает точный результат.

Квадратурные формулы Гаусса

Поскольку формулы Ньютона - Котеса являются интерполяционными, очевидно, что они не могут успешно использоваться для получения формул высокой точности по причине неустойчивости интерполяционного процесса для многочленов высокого порядка. По этой причине обычно используются полиномы степени от нуля до трех (соответственно, формулы прямоугольников со средней точкой, трапеций, Симпсона). Вычисление с их помощью интегралов от функций, обладающих высокой степенью гладкости, например, близким к полиномам высокой степени, представляется нерациональным. В выражение для погрешности этих формул входят первая, вторая или четвертая производные. Погрешность определяется низким порядком производной при высокой степени гладкости интегрируемой функции. Этих недостатков лишены квадратуры Гаусса.

Формулировка задачи построения квадратурных формул, поставленная Гауссом, такова.

Для заданного количества точек, а именно, для (N + 1) точки, найти такое расположение узлов и такие веса c_i, чтобы квадратурная формула

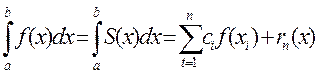
была точной для полиномов как можно более высокой степени

Пусть отрезок интегрирования [a,b] непрерывной функции f(x) разбит на n равных частей точками 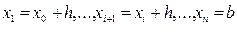(h – шаг разбиения 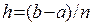. Обозначим через S(x) сплайн-функцию, аппроксимирующую подынтегральную функцию f(x).

Пусть на каждой части разбиения [x_i-1 ,x_i] (i=1,2,…,n) расположено m узлов [x_i1,…,x_im] , в которых подынтегральная функция f(x) на каждой i-й части аппроксимируется многочленом 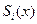степени p, х Є [x_i-1,…,x_i], (i=1,2,…,n). При этом на многочлен 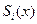накладываются 2 ограничения:

а) значения многочлена и подынтегральной функции равны в узлах интерполяции: S_i(x_ij)=f(x_ij) (i=1,…,n; j=1,…,m);

б) определенный интеграл от функции 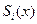на отрезке [x_i-1, x_i] выражается через значения подынтегральной функции f(x_ij) в узлах в виде их линейной комбинации

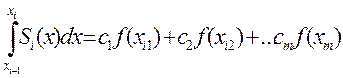(4)

Квадратурные формулы Гаусса для выбранной степени p сплайна будут определены, если из условий а) и б) удастся найти m неизвестных коэффициентов c_i и координаты m узлов x_ij ( j=1,…,m).

Задача решается одновременно для всех n частей разбиения отрезка [a,b] , если выразить х Є [x_i-1,…,x_i], (i=1,2,…,n) через переменную t Є [-1;1]:

;

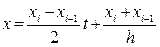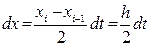
Положим ; ;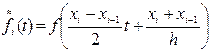

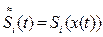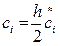
Тогда 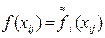(i=1,…,n; j=1,…,m) и соотношение (4) перепишем в виде

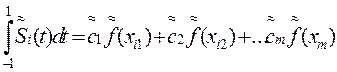(5)

Выведем квадратурную формулу Гаусса с тремя узлами (m=3). Для этого необходимо определить шесть величин: 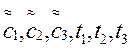. Функция 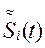-многочлен степени p, общий вид которого

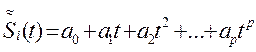(6)

Подставив соотношение (6) и (5) и учитывая, что 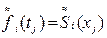(j=1,2,3,…,p), получим тождество относительно коэффициентов a_k (k=0,1,2,…,p):

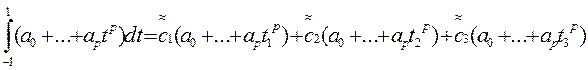
Шесть неизвестных будут определены однозначно из системы шести уравнений. В общем случае степень p аппроксимирующего многочлена всегда является нечетным числом и связана с числом узлов m соотношением p=2m-1. В частности, для трех узлов имеем многочлен пятой степени.

Множители при a_k в левой части тождества вычисляется так:

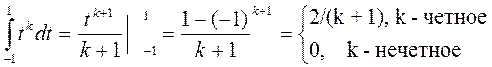
Приравняем подобные выражения в левых и правых частях тождества при одинаковых коэффициентах 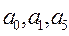. Получим:

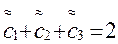
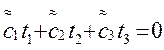
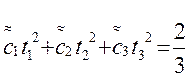
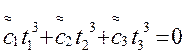(7)

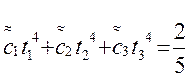
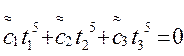
Эту систему позволяет упростить следующее свойство ее решения: неизвестные t_i (i=1,2,…,m) системы 2m уравнений вида

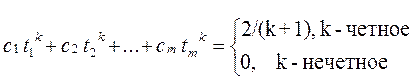
где k=0,1,…,2m-1 являются нулями многочлена Лежандра 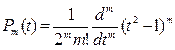; нули принадлежат интервалу (-1;1) и расположены симметрично относительно середины интервала. В нашем случае m=3 и 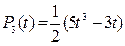. Находим нули многочлена из уравнения 5t³-3t=0. Подставив корни уравнения 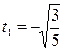, t₂=0, 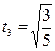в (7), получим систему трех линейных уравнений относительно переменных :

, ,

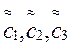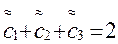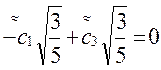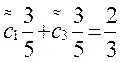
Теперь подставим найденные значения в соотношение (4):

,

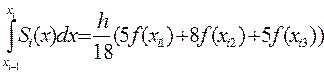где , , .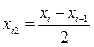

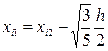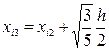Итак, квадратурная формула Гаусса с тремя узлами записывается в виде

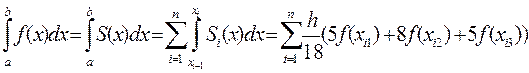
Если подынтегральная функция имеет непрерывную производную шестого порядка, то для оценки погрешности формулы Гаусса с тремя узлами можно использовать неравенство:

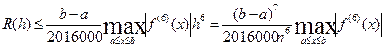
При вычислении интеграла до достижения заданной точности ε методом двойного пересчета условие окончания вычислений имеет вид

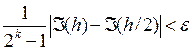,где k=2m (m – число узлов в квадратурной формуле Гаусса). Полагают, что 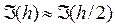с точностью ε. Формулы Гаусса обеспечивают высокую точность уже при небольшом количестве узлов.

Блок-схемы решения задачи рассмотренными методами приведены на рис. 5.4 и 5.5.

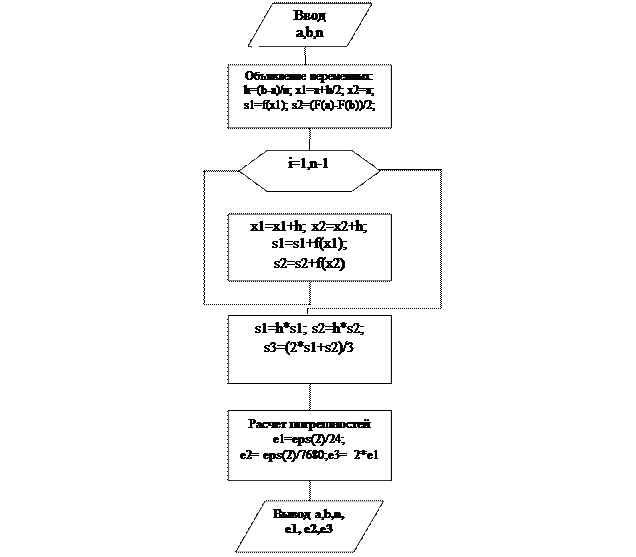
Рис. 5.4 Вычисление определенного интеграла по квадратурным формулам прямоугольников, трапеций и Симпсона

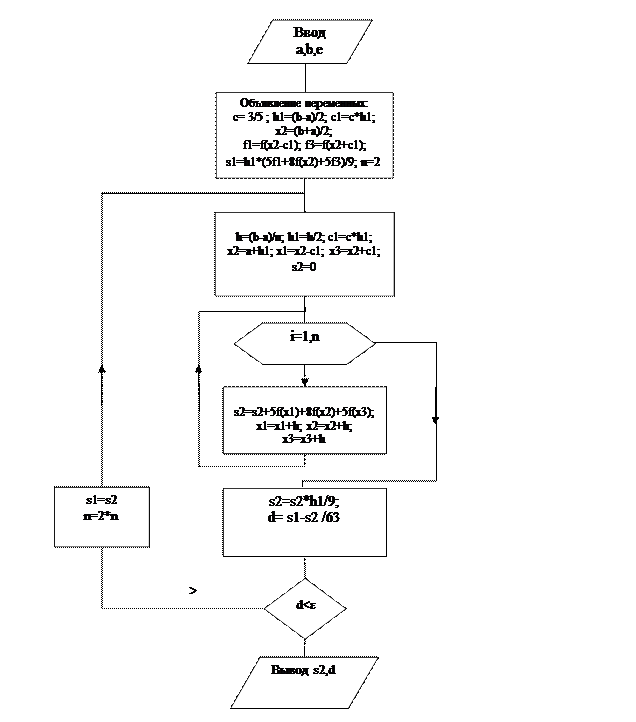
Рис. 5.5 Вычисление определенного интеграла методом двойного пересчета по формуле Гаусса с тремя узлами

Лабораторная работа 6