Интегрирование тригонометрических функций (универсальная тригонометрическая подстановка, расчеты). 3.6
Вопросы к экзамену по математическому анализу для групп 1БЭС
( 1-й семестр)
Понятие последовательности. Символы математической логики. Понятие предела последовательности. Геометрический смысл. Символическая запись. 1.1
Последовательности бесконечно малые и бесконечно большие - определения. Теорема о произведении бесконечно малой последовательности на ограниченную. Неопределенности и рекомендации по раскрытию неопределенностей. Теорема Больцано-Вейерштрасса. Второй замечательный предел. Число Эйлера. 1.1
Теорема Больцано-Вейерштрасса. Второй замечательный предел. Задача о непрерывном начислении процентов (вывод). 1.2
Понятие основной элементарной функции, элементарной функции. Примеры неэлементарных функций, их графики. 1.3
Предел функции, символическая запись. Методы вычисления пределов функций. Первый замечательный предел. 1.3,1.4
6. Сравнение бесконечно малых (разбор трех ситуаций). Символ “o- маленькое”. Теорема об эквивалентных бесконечно малых. Таблица основных эквивалентностей. 1.5
Асимптоты графика функции. Нахождение вертикальной и наклонной асимптот. 1.6
Асимптоты графика функции. Нахождение вертикальной и наклонной асимптот. 5.9.
Понятие непрерывной функции в точке а. Эквивалентное определение непрерывности в точке. Блок схема исследования на непрерывность. 1.7
Теорема об ограниченности непрерывной функции, графическая иллюстрация. Замечание. Доказательство теоремы об устойчивости знака непрерывной функции. 1.8
Теорема Больцано-Коши. Графическая иллюстрация. Геометрический смысл. Теорема о промежуточном значении непрерывной функции. Графическая иллюстрация. Теорема Вейерштрасса, графическая иллюстрация. 1.8
Понятие производной. Правая и левая производные. Производная сложной функции. Логарифмическое дифференцирование. 2.1
Правило Лопиталя. Производная функции заданной параметрически. Вторая производная. Производная неявной функции. 2.2, 2.3
Геометрический смысл производной. Уравнение касательной (два случая). Понятие нормали. Ее уравнение. Графическая иллюстрация (разбор четырех случаев). 2.4
Экономический смысл производной. Понятие эластичности. Расчетная формула. 2.5
Понятие дифференцируемой функции. Дифференциал. Применение дифференциала в приближенных вычислениях. Геометрический смысл дифференциала. 2.6
Доказательство теоремы Ферма. Геометрический смысл. Необходимое условие экстремума. 2.7
Теорема Лагранжа, геометрический смысл. Следствия. Теорема Ролля, геометрический смысл. Физический смысл теоремы Лагранжа. 2.7
Понятия локального максимума и локального минимума. Точки экстремума. Первое достаточное условие экстремума. 2.8
Понятия локального максимума и локального минимума. Второе достаточное условие экстремума. Исследование на экстремум с помощью высших производных. 2.8
Наибольшее и наименьшее значения функции непрерывной на отрезке. 2.9
22. Исследование поведения функции в окрестности точки х0. Формула Тейлора. Правило определения степени n. Формула Маклорена. 2.10
Кривые выпуклые вверх и вниз, связь со второй производной. Точки перегиба. Основные шаблоны точек перегиба. 2.11
Этапы исследования функции с целью построения ее графика. 2.12
25. Понятие первообразной, ее непрерывность, доказательство теоремы об общем виде первообразных. Неопределенный интеграл и обзор таблицы (вывод одной из формул - по выбору преподавателя). 3.1
Нахождение неопределенных интегралов методом занесения под дифференциал. Метод замены переменной. 3.2, 3.3
Формула интегрирования по частям. 3.4
Интегрирование рациональных дробей (правильные и неправильные дроби, разложение на простейшие дроби, метод неопределенных коэффициентов). 3.5
Интегрирование тригонометрических функций (универсальная тригонометрическая подстановка, расчеты). 3.6
Образец экзаменационного билета
(время на подготовку 1,5 часа)
МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № * Дисциплина Математический анализ______________________________________ Факультет Экономический курс 1 группы 1бэс 1. ТЕОРИЯ: Нахождение неопределенных интегралов методом занесения под дифференциал. Метод замены переменной. 2. ЗАДАЧИ: а) найти предел последовательности 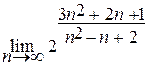 б) найти производную функции б) найти производную функции 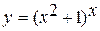 в) верно ли утверждение x = о (х 2) при х → 0 ? Ответ обосновать. г) исследовать на непрерывность функцию: в) верно ли утверждение x = о (х 2) при х → 0 ? Ответ обосновать. г) исследовать на непрерывность функцию: 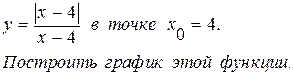 д) д) 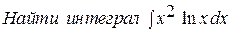 |
