Универсальная тригонометрическая подстановка.

Типовые задания. Неопределенный интеграл

В каждом задании предлагается найти семь интегралов. Согласно порядковому номеру в задании, для вычисления интеграла, предполагается применить вполне определенную подстановку из некоторого класса или другой способ интегрирования. Для удобства ниже приводятся образцы решений на подобный вариант. При затруднении можно обратиться к соответствующему параграфу настоящей главы и желательно просмотреть соответствующие параграфы в [2, 12, 17].

Образцы решений

Интегрирование подстановкой

Пример 1.1. 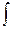cosx sin²x dx

►. Пользуясь тем, что dsinx = cosx перепишем данный интеграл

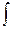. sin²x dsinx=(sin³x)/3+c. ◄

Пример 1.2.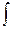

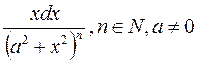
► Сделаем замену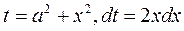

◄

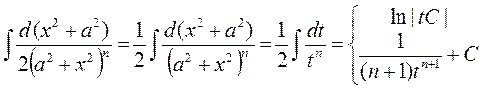Интегрирование по частям

Пример 2.1. 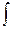x2^xdx

► применим метод интегрирования по частям .

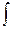uv`dx = uv-. 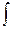vu`dx)

Положим здесь u = x,v`=2^x. Тогда получим:

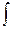. x2^xdx = x2^xlog₂e - 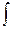2^xlog₂e dx = x2^xlog₂e – 2^x(log₂e)² +c◄

Пример 2.2. 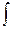arccos²xdx

► положим здесь u = arccos²x, dv = dx, тогда

du = 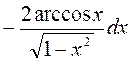, v = x.

Согласно формуле интегрирования по частям

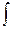. arccos²xdx = xarccos²x+2. ,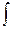

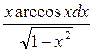Для вычисления полученного интеграла еще раз воспользуемся формулой интегрирования по частям

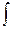
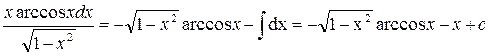
Подставляя в выражение для первоначального интеграла, получаем:

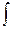. arccos²xdx = xarccos²x – 2 ◄

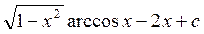Пример 2.3. .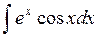

► Положим u = cosx, v`= e^x и применим формулу интегрирования по частям

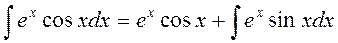
Теперь к интегралу 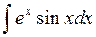применим формулу интегрирования по частям:

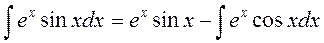
Обозначая исходный интеграл через I получаем следующее уравнение:

. I = e^xcosx + e^xsinx – I

разрешая которое относительно I получаем выражение для I

. ◄

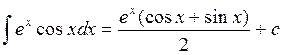Пример 2.4.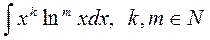

► возьмем 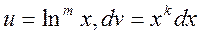тогда

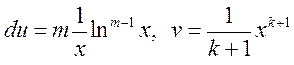
и мы получаем рекуррентную формулу

,

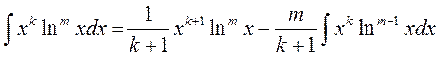если к – вещественное, формула остается справедливой. Проводя интегрирование по частям до «полного исчезновения» логарифма, мы найдем наш интеграл. Подстановка 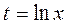а сводит этот интеграл к следующему

◄

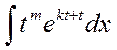3. Метод интегрирования рациональных дробей:

Пример 3.1. .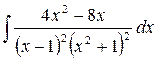

► Разложение подынтегральной функции на элементарные дроби имеет вид

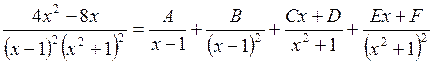
Следовательно,

4x² – 8x = A(x – 1)(x² + 1)² + B(x² + 1) ² + (Cx + D)(x – 1)²(x² + 1) + (Ex +F)(x – 1)²

Приравняв соответствующие коэффициенты этих многочленов, можно получить систему шести линейных уравнений с шестью неизвестными и решить ее. Но проще поступить иначе. Положив в данном равенстве x = 1, найдем B = –1. Затем положим x = i, тогда будем иметь:

-4 – 8i = (Ei + F)(i – 1)² = 2E – 2iF.

Приравнивая действительные и мнимые части, получим

–4 = 2E,-8 = –2F, т.е. E = –2, F = 4.

Продифференцируем обе части равенства (разложения подынтегральной функции на элементарные дроби), причем будем выписывать только слагаемые не равные нулю, при x = 1. Тогда получим

8x – 8 = A(x² + 1)² + 2B(x² + 1)2x+…

Отсюда при х = 1 имеем 0 = 4A + 8B, т.е. A = 2. Теперь продифференцируем обе части равенства, выписывая только те слагаемые, которые не равны нулю при x = i.

8x – 8 = (Cx + D)(x – 1)²2x + E(x – 1)² + (Ex + F)2(x – 1) + …

Подставив в это равенство x=i, найдем последние 2 коэффициента:

C = –2, D = –1. Таким образом,

.

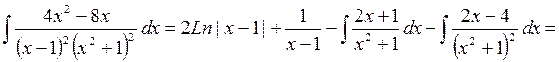
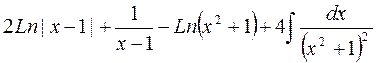Последний интеграл находим пользуясь рекуррентной формулой, выведенной в примере на интегрирование по частям

.

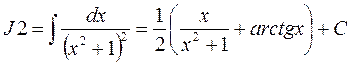В итоге получаем

.◄

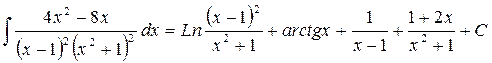Универсальная тригонометрическая подстановка.

Пример 4.1. .I=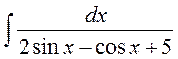

►Положим t = tg(x/2), (2n – 1) p < x < (2n + 1)p (n = 0;±1; ±2;…), получаем:

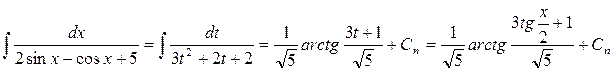
Из непрерывности первообразной следует:

I(2pn+p-0)=I(2pn+p+0),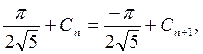

откуда находим 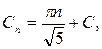где С = С₀ – произвольная постоянная.

Из неравенств 2pn < x + p < (2n + 2)p; n < (x + p )/2p < n+1 следует, что

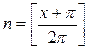. Таким образом,

I=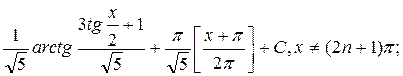

I= 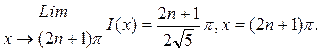◄