Независимость собственных векторов
Теорема. Собственные векторы 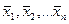 оператора, отвечающие различным собственным значениям λ1λ2…..λn линейно независимы. Важнейшее следствие: определитель матрицы не зависит от выбора базиса.
оператора, отвечающие различным собственным значениям λ1λ2…..λn линейно независимы. Важнейшее следствие: определитель матрицы не зависит от выбора базиса.
Доказательство.Пусть 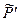 - оператор в новом базисе, тогда
- оператор в новом базисе, тогда
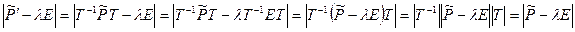
т.е. при переходе к новому базису собственные числа сохраняются. Наиболее простой вид принимает матрица P линейного оператора 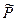 , имеющего n линейно независимых собственных векторов
, имеющего n линейно независимых собственных векторов 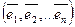 с собственными значениями λ1,λ2…λn .Векторы
с собственными значениями λ1,λ2…λn .Векторы 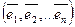 примем за базисные. Тогда разложение векторов
примем за базисные. Тогда разложение векторов 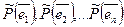 по базису
по базису 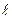 1,
1, 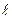 2...
2... 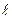 n как это следует из свойств линейных операторов, примет вид :
n как это следует из свойств линейных операторов, примет вид :
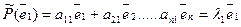
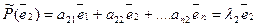
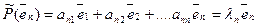
Отсюда следует, что 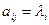 если i=j и aij=0 если i ≠ j. Таким образом, в базисе составленном из собственных векторов, матрицы оператора будет иметь диагональный вид.
если i=j и aij=0 если i ≠ j. Таким образом, в базисе составленном из собственных векторов, матрицы оператора будет иметь диагональный вид.
P= 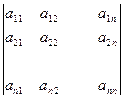 =
= 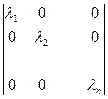
Верно и обратное если матрица P линейного оператора 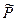 в некотором базисе является диагональной, то все векторы этого базиса- собственные векторы оператора
в некотором базисе является диагональной, то все векторы этого базиса- собственные векторы оператора 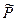 .
.
Симметричный оператор.
Линейный оператор 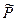 называется симметричным, если для любых векторов
называется симметричным, если для любых векторов 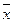 и
и 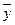 выполняется равенство:
выполняется равенство: 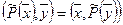 .
.
Теорема. Для того, чтобы линейный оператор был симметричен, необходимо и достаточно, чтобы его матрица в ортогональном пространстве была симметрична.
Рассмотрим для простоты двухмерное пространство. Линейные операторы 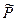 1 и
1 и 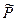 2 определены своими матрицами
2 определены своими матрицами
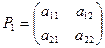 и
и 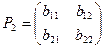
Вычислим векторы 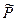 1(
1( 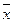 ) и
) и 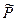 2(
2( 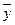 )
)
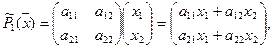
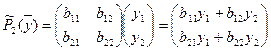
Найдем скалярные произведения 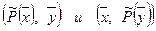 :
:
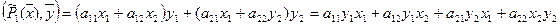
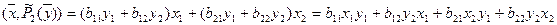
Найдем разность скалярных произведений:
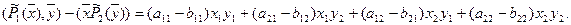 (1)
(1)
Если эта разность равна 0, то будут выполняться равенства (необходимость)
 11= b11,
11= b11,  21 = b12,
21 = b12, 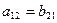 ,
,  22=b22 (2) и обратно, если только что записанные соотношения выполнены для любых
22=b22 (2) и обратно, если только что записанные соотношения выполнены для любых 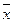 и
и 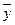 , то и равенство (1) выполнено (достаточность). Система равенств (2) означает, что
, то и равенство (1) выполнено (достаточность). Система равенств (2) означает, что 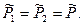
Ортогональность собственных векторов.
Теорема: собственные векторы симметричного линейного оператора, соответствующие различным собственным числам, взаимно ортогональны.
Пусть векторы 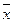 и
и 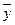 - собственные векторы оператора
- собственные векторы оператора 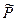 соответствующие собственным числам λ1 и λ2, причем λ1≠λ2 . По определению симметричного оператора:
соответствующие собственным числам λ1 и λ2, причем λ1≠λ2 . По определению симметричного оператора:
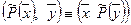 . Подставляя сюда
. Подставляя сюда 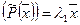 и
и 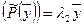 получим
получим 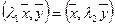 . Вынесем λ1 и λ2 за знак скалярного произведения, перенесем все влево и разложим на множители и получим
. Вынесем λ1 и λ2 за знак скалярного произведения, перенесем все влево и разложим на множители и получим 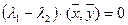 , так как λ1≠λ2 , то
, так как λ1≠λ2 , то 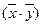 =0, что означает взаимную ортогональность векторов
=0, что означает взаимную ортогональность векторов 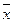 и
и 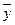 .
.
Квадратичные формы.
Пусть L=( 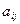 )- симметричная матрица n-го порядка, тогда выражение
)- симметричная матрица n-го порядка, тогда выражение 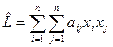 -называется квадратичной формой переменных x1,x2...xn. Матрица L=(
-называется квадратичной формой переменных x1,x2...xn. Матрица L=(  ij) i,j=(1,2...n) -называется матрицей квадратичной формы. Пусть(
ij) i,j=(1,2...n) -называется матрицей квадратичной формы. Пусть( 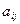 ) –симметричная матрица, т.е.
) –симметричная матрица, т.е. 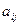 =
= 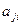 . В матричной форме квадратичная форма имеет вид :
. В матричной форме квадратичная форма имеет вид :
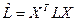 , где X=
, где X= 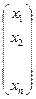 -матрица столбец переменных, а
-матрица столбец переменных, а 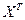 =
= 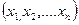 - матрица строка этих же переменных. Найдем произведение этих матриц.
- матрица строка этих же переменных. Найдем произведение этих матриц.
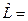
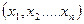
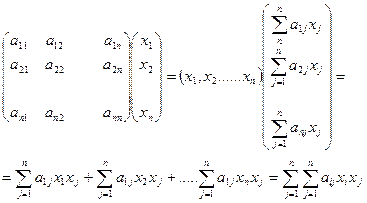
-что является по определению квадратичной формой.
