Элементы векторной алгебры и аналитической геометрии
Задание №5 (экономисты – бакалавры не выполняют)
Вариант 1. Найти уравнение параболы, проходящей через точку (6,9), с вершиной в начале координат и симметричной относительно оси Оу.
Вариант 2. Ось Ох – ось симметрии параболы с вершиной в начале. Найти уравнение этой параболы, зная, что она проходит через точку (2,2).
Вариант 3. Фокусы эллипса делят расстояние между директрисами на три равные части. Найти его эксцентриситет.
Вариант 4. Директрисы гиперболы делят расстояние между фокусами на три равные части. Найти ее эксцентриситет.
Вариант 5. Ординаты окружности x2+y2=36 уменьшены в два раза. Найти уравнение полученной кривой.
Вариант 6. Найти полуоси эллипса 3x2+5y2 –30=0.
Вариант 7. На параболе y2=24x взята точка на расстоянии 14 ед. от фокуса. Определить ее расстояние от вершины.
Вариант 8. Дана парабола y2=4-4x и прямая x+y=1 . Через одну из точек их пересечения провести другую параболу с той же осью и фокусом.
Вариант 9. Даны две точки, лежащие на эллипсе. Оси которого служат осями координат (3,2,4) и (4,1,8). Найти этот эллипс и проекции фокусов на хорду, соединяющую данные точки.
Вариант 10. Даны три точки (-5,2), (1,-4), (5,12), лежащие на параболе с осью, параллельной оси Оу. Найти вершину. Фокус и директрису этой параболы.
Вариант 11. Найти уравнение эллипса , проходящего через точки (1,4) и (7,2) и симметричного относительно осей Ох и Оу.
Вариант 12. Расстояние между фокусами эллипса равно 2, расстояние между директрисами 10. Найти оси.
Вариант 13. Составить каноническое уравнение параболы, если ее фокус имеет координаты (0; -3).
Вариант 14. Составить каноническое уравнение эллипса, если его эксцентриситет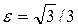 
, большая полуось а = 3.
Вариант 15. Составить каноническое уравнение гиперболы, если расстояние между фокусами равно 10, а расстояние между вершинами равно 8.
Вариант 16. Составить каноническое уравнение эллипса, зная, что расстояние между фокусами равно 24 и большая полуось равно 26.
Вариант 17. Составить каноническое уравнение гиперболы, если действительная полуось равна 5 и эксцентриситет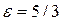 
.
Вариант 18. Составить каноническое уравнение параболы, директриса которой имеет уравнение x + 2 = 0.
Вариант 19. Составить каноническое уравнение эллипса, если большая полуось равна 5, а расстояние между фокусами – 8.
Вариант 20. Составить каноническое уравнение гиперболы, если она равносторонняя и проходит через точку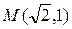 
.
Вариант 21. Составить каноническое уравнение параболы, фокус которой имеет координаты (-5; 0).
Вариант 22.Составить каноническое уравнение эллипса, если большая полуось равна 10 и эксцентриситет равен 0,8.
Вариант 23.Составить каноническое уравнение гиперболы, асимптоты которой заданы уравнениями y=±2x и фокусы находятся на расстоянии, равном 5 от центра.
Вариант 24.Составить каноническое уравнение параболы, симметричной относительно оси ординат и проходящей через точку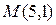 
.
Задание № 6
При каких значениях k вектора a и b перпендикулярны?
a={k*№ варианта, № варианта-10, № варианта-5}
b={k*(№ варианта-10), k*№ варианта, 1}
Задание № 7
По трем заданным точкам построить треугольник и средствами векторной алгебры найти:
1) длину стороны ВС;
2) уравнение линии ВС;
3) угол между сторонами ВА и ВС;
4) координаты точки N – середины стороны АС;
Координаты вершин треугольника даны в таблице.
| № варианта | А | В | С | № варианта | А | В | С |
| (-2, 5) (4, 5) (1, 1) | (4, 9) (2, 4) (5, 7) | ||||||
| (-3, 1) (4, -5) (7, 2) | (6, 9) (5, -4) (4, 6) | ||||||
| (4, -1) (4, 4) (6, 4) | (2, 3) (4, 0) (5, 3) | ||||||
| (-5, 3) (4, 6) (8, 4) | (8, 7) (3, 0) (5, 6) | ||||||
| (0, -6) (3, 5) (-2, 4) | (8, 1) (3, 0) (3, 5) | ||||||
| (-2, -3) (10, 6) (5, 2) | (1, 3) (7, 10) (3, 2) | ||||||
| (-6, 2) (1, 8) (4, 5) | (4, 0) (6, 9) (-2, 1) | ||||||
| (1, 5) (6, 5) (5, 7) | (-2, 1) (-2, 5) (4, 0) | ||||||
| (5, -2) (7, 2) (5, 5) | (-2, 1) (-3, 1) (4, 10) | ||||||
| (5, -2) (8, 4) (6, 5) | (1, -2) (4, -1) (6, 9) | ||||||
| (9, 6) (2, 3) (4, 0) | (4, 7) (3, 2) (2, 3) | ||||||
| (7, 5) (4, 0) (1, 2) | (7, 3) (0, 6) (6, 8) |
Задание 8
По четырем заданным точкам построить пирамиду и средствами векторной алгебры найти:
1) длину ребра А1 А 2;
2) угол между ребрами А1 А 2 и А1 А 4;
3) площадь грани А1 А2 А3;
4) объем пирамиды А1 А2 А3 А4;
5) уравнение плоскости А1 А2 А3.
6) нормальный вектор плоскости А1 А2 А3
7) уравнение прямой, походящей через точку А4 перпендикулярно плоскости А1 А2 А3.
Координаты вершин пирамиды даны в таблице.
| № варианта | А1 | А2 | А3 | А4 |
| (1, 1, 1) (-1, 2, 4) (2, 0, 6) (-2, 5, -1) | ||||
| (0, 5, 0) (2, 3, -4) (0, 0, -6) (-3, 1, -1) | ||||
| (0, 0, 6) (4, 0, -4) (1, 3, -1) (4, -1, -3) | ||||
| (2, -5, 3) (3, 2, -5) (5, -3, -2) (-5, 3, 2) | ||||
| (6, 0, 4) (0, 6, 4) (4, 6, 0) (0, -6, 4) | ||||
| (3, 2, 4) (2, 4, 3) (4, 3, -2) (-2, -4, -3) | ||||
| (6, 3, 5) (5, -4, 3) (3, 5, 6) (-6, -1, 2) | ||||
| (5, -2, -1) (4, 0, 0) (2, 5, 1) (1, 2, 5) | ||||
| (4, 2, 5) (3, 0, 4) (0, 0, 3) (5, -2, -4) | ||||
| (4, 2, -5) (3, 0, 4) (0, 2, 3) (5, -2, -4) | ||||
| (4, 4, 10) (7, 10, 2) (2, 8, 4) (9, 6, 9) | ||||
| (4, 6, 5) (6, 9, 4) (2, 10, 10) (7, 5, 9) | ||||
| (3, 5, 4) (8, 7, 4) (5, 10, 4) (4, 7, 8) | ||||
| (10, 6, 6) (-2, 8, 4) (6, 8, 9) (7, 10, 3) | ||||
| (1, 8, 2) (5, 2, 6) (5, 7, 4) (4, 10, 9) | ||||
| (6, 6, 5) (4, 9, 5) (4, 6, 11) (6, 9, 3) | ||||
| (7, 2, 2) (5, 7, 7) (5, 3, 1) (2, 3, 7) | ||||
| (8, 6, 4) (10, 5, 5) (5, 6, 8) (8, 10, 7) | ||||
| (7, 7, 3) (6, 5, 8) (3, 5, 8) (8, 4, 1) | ||||
| (-2, 1, 2) (4, 0, 0) (3, 2, 7) (1, 3, 2) | ||||
| (3, 2, 7) (1, 3, 2) (-2, 1, 2) (4, 0, 0) | ||||
| (1, 3, 2) (3, 2, 7) (4, 0, 0) (-2, 1, 2) | ||||
| (3, 1, -2) (1, -2, 1) (2, 2, 5) (-2, 1, 0) | ||||
| (-2, 1, 0) (2, 2, 5) (3, 1, 2) (1, -2, 1) |
Литература
1. Высшая математика для экономистов: Учебник для ВУЗов/Под ред. Н.Ш Кремера. – М.: ЮНИТИ, 2001. – 472 с.
2. Кириллов А.Л. Математика для управленцев: Курс лекций. – СПб., 2000. – 240 с.
3. Ибатуллина С.М. Математика. Учебно-методический комплекс. –Уфа, БАГСУ, 2007. - 91 с.
4. Ефимов А.В., Демидович Б.П. Сборник задач по математике для втузов: линейная алгебра и основы математического анализа. – М.: Наука, 1981, 1986, ч.ч. 1,2,3.
5. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, 1978.
6. Рабочая тетрадь по высшей математике «Элементы линейной алгебры и комплексные числа». Ч.1. – Уфа: РИО БАГСУ, 2000. – 25 с.
7. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М.: Наука, 1968.
8. Карасев А.И., Аксютина З.М., Савельева Т.М. Курс высшей математики для экономических вузов. – М.: Высшая школа, 1982.
9. Клетеник Д.В. Сборник задач по аналитической геометрии. – М.: Наука, 1986.
10. Рабочая тетрадь по высшей математике «Элементы векторной алгебры и аналитической геометрии». Ч.2. – Уфа: РИО БАГСУ, 2000. – 32 с.