Определение реакций в кинематических парах группы Ассура (2-3)

Вычерчиваем схему группы (μ_l = 0,00667 м/мм ) и прикладываем к звеньям группы все известные силы и моменты.

К звену 3: R₄₃ = -R₃₄ = 2084,8 Н; G₃= 784 Н; F_и3' = 656,6 Н.

Вектор R₄₃ прикладываем в точке B, развернув вектор R₃₄ на 180˚.

К звену 2 прикладываем: G₂= 441 Н; F_и2' = 379,1 Н.

В раскрытых кинематических парах прикладываем реакции. Реакцию R₀₃ представляем в виде нормальной и касательной составляющих Rⁿ₀₃ и R^τ₀₃ (Rⁿ₀₃ направим вдоль ВЕ, а R^τ₀₃ - перпендикулярно ВЕ). Реакцию R₁₂ представляем в виде нормальной и касательной составляющих Rⁿ₁₂ и R^τ₁₂ (Rⁿ₁₂ направим вдоль АВ, а R^τ₁₂ - перпендикулярно АВ)

Величину R^τ₀₃ определим из уравнения моментов всех сил, действующих на звено 3, относительно точки В (центрального шарнира группы):

ΣM_В³(F_i) = R^τ₀₃·ОВ +F_и3'·h₅ -R₄₃·h₆ = 0 ,

откуда

R^τ₀₃ = (-F_и3'·h₅ +R₄₃·h₇)/ ОВ =

= (-656,6×21,4 + 2084,8×115,96)/120 = 2022 Н

Поскольку знак R^τ₀₃ из уравнения получен положительным, значит предварительное направление этой составляющей реакции на листе выбрано верно.

Величину R^τ₁₂ определим из уравнения моментов всех сил, действующих на звено 2, относительно точки В (центрального шарнира группы):

ΣM_В²(F_i) = R^τ₁₂·АВ- F_и2'·h₄ -G₂·h₃ = 0 ,

Откуда

R^τ₁₂ = (G₂·h₃ +F_и2'·h₄)/ АВ = ( 441·18,64+379,1·67,99)/180 = 188,86 Н

Поскольку знак R^τ₁₂ из уравнения получен положительным, значит предварительное направление этой составляющей реакции на листе выбрано верно.

Поскольку направления реакций Rⁿ₀₃ и Rⁿ₁₂ известны, то, применяя принцип Даламбера, записываем условие равновесия группы Ассура

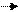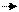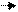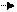Rⁿ₀₃ + R^τ₀₃ + G₃ +F_и3' + R₄₃ + F_и2' + G₂ + R^τ₁₂ + Rⁿ₁₂ = 0 .

Выбрав масштаб К_Р = 20 Н/мм, строим план сил для группы 2-3, последовательно откладывая векторы сил и замыкая силовой многоугольник от точки пересечения направлений неизвестных реакций Rⁿ₀₃ и Rⁿ₁₂.

С учетом масштаба величины реакций

R₁₂ = 228,5·20 = 4570 Н;

R₀₃ = 116,5·20 = 2330 Н.

Силовой расчет ведущего звена

Проводим силовой расчет ведущего звена.

Прикладываем в т. А реакцию R₂₁ =341 Н, G₁=118 H, F_и1¢=64,8 Н развернув вектор R₁₂ на 180˚, а также уравновешивающую силу F_ур перпендикулярно звену.

Величину уравновешивающей силы находим из уравнения моментов относительно т. O:

-F_ур·ОА + R₂₁·h₈ +G₁×h₉= 0,

откуда

F_ур = (R₂₁·h₈+ G₁×h₉)/ОА =(4570×17,79+118×15,91)/45= 1848,4 H.

Выбрав масштаб К_Р = 10 Н/мм, строим план сил для звена 1 по уравнению F_ур + R₂₁ + F_и1¢+G₁+R₀₁ = 0, и определяем из плана сил величину реакции

R₀₁ = 224·10 = 2240 Н.

Выводы

В результате выполнения курсового проекта произведен кинематический, силовой и динамический анализ механизма. В кинематическом расчете определены линейные скорости и ускорения характерных точек, а также угловые скорости и ускорения звеньев механизма.

В ходе силового анализа рассчитаны реакции в кинематических парах, значения которых могут быть использованы при последующих прочностных расчетах звеньев механизма.

Динамический анализ позволил путем создания динамической модели механизма (приведения механизма к входному звену) построить диаграмму энергомасс и с ее помощью рассчитать размеры маховика, обеспечивающего требуемую неравномерность движения механизма.

На четвертом листе построили картину зацепления зубчатых колес, рассчитали коэффициент удельного скольжения. Также подобрал количество чисел зубьев планетарного редуктора, для обеспечения заданного передаточного числа привода механизма конвейера.

В целом выполнение курсового проекта помогло освоить наиболее употребляемые графические и графоаналитические методы анализа и синтеза механизмов.

Литература

1. Езерская С.В., Янченко Т.А., Аллилуева Л.А. Аналитическое исследование кинематически плоских рычажных механизмов с применением ЭВМ: Методические указания к выполнению курсового проекта по теории механизмов и машин. – Ижевск: ИМИ, 1989 – 42с.

2.Андрющенко В.М. Матиматические таблицы для расчета зубчатых передач. – М.: Машиностроение, 1974. – 440 с.

3.Болотовская Т.П., Болотовский И.А., Смирнов В.Э. Справочник по корригированию зубчатых колес. – М.: Машгиз, 1962 – 215 с.

4.Артоболевский И.И. Теория механизмов и машин. – М.: Наука, 1975. -639 с.

5.Кореняко А.С. и др. Курсовое проектирование по теории механизмов и машин. – Киев: Вища школа, 1970 – 332 с.

6.Попов С.А. Курсовое проектирование по теории механизмов и механике машин: Учеб. Пособие для машиностроит. спец. вузов / Под ред. К.В. Фролова. – М.: Высш. шк., 1986 – 295 с.

7.Фролов К.В., Попов С.А., Мусатов А.К. и др. Теория механизмов и машин. – М.: Высш. шк., 1987. – 496 с.