Изучение затухающих колебаний
В ЭЛЕКТРИЧЕСКОМ КОНТУРЕ
Цель работы: изучение затухающих колебаний в электрическом контуре и определение параметров контура.
1. Теория
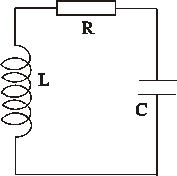
|
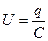 , где С – емкость конденсатора. Воспользуемся вторым правилом Кирхгофа (законом Ома для неоднородного участка цепи), согласно которому сумма падений напряжений в замкнутом контуре равна сумме имеющихся в контуре ЭДС. В рассматриваемом контуре действует ЭДС самоиндукции
, где С – емкость конденсатора. Воспользуемся вторым правилом Кирхгофа (законом Ома для неоднородного участка цепи), согласно которому сумма падений напряжений в замкнутом контуре равна сумме имеющихся в контуре ЭДС. В рассматриваемом контуре действует ЭДС самоиндукции 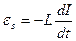 , возникающая в катушке индуктивности при изменении силы тока. Следовательно, уравнение Кирхгофа для данного колебательного контура имеет вид:
, возникающая в катушке индуктивности при изменении силы тока. Следовательно, уравнение Кирхгофа для данного колебательного контура имеет вид: 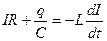 (1)
(1)
Здесь I – сила тока в цепи. С учетом того, что ток 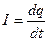 , уравнение (1) может быть преобразовано к следующему виду:
, уравнение (1) может быть преобразовано к следующему виду:
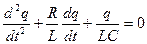 (2)
(2)
с учетом обычно применяемых обозначений 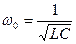 (собственная циклическая частота колебательного контура) и
(собственная циклическая частота колебательного контура) и 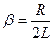 , уравнение (2) можно переписать в виде:
, уравнение (2) можно переписать в виде:
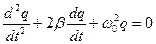 (3)
(3)
Это уравнение позволяет описать динамику изменения заряда конденсатора в рассматриваемом контуре в отсутствие внешней ЭДС.
2. Свободные колебания в контуре без активного сопротивления.
Если активное сопротивление контура R равно нулю, то коэффициент 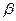 также равен нулю и уравнение (3) превращается в уравнение свободных колебаний:
также равен нулю и уравнение (3) превращается в уравнение свободных колебаний:
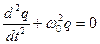 (4)
(4)
Решением этого уравнения является гармоническая функция:
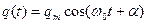 (5)
(5)
В этом легко убедиться путем подстановки (5) в (4), которая превращает (4) в тождество.
Основное свойство колебательных движений – повторяемость через равные промежутки времени. Математически это означает:
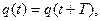 (6)
(6)
где Т – период колебаний. Воспользовавшись явным видом зависимости 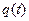 (5) мы получим:
(5) мы получим:
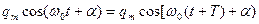 (7)
(7)
Учитывая, что период функции косинус равен 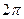 , соотношение будет выполняться, если аргументы косинусов в левой и правой частях соотношения (7) отличаются на
, соотношение будет выполняться, если аргументы косинусов в левой и правой частях соотношения (7) отличаются на 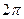 . После несложных преобразований получаем:
. После несложных преобразований получаем:
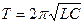 (8)
(8)
Соотношение (8) носит название формула Томсона. Из (5) можно получить выражения для напряжения на конденсаторе U и силы тока в контуре I:
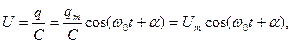 (9)
(9)
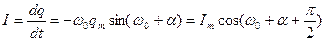 (10)
(10)
где 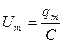 и
и 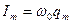 – максимальные значения напряжения и силы тока,
– максимальные значения напряжения и силы тока, 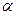 – начальная фаза колебаний. Таким образом, заряд на обкладках конденсатора изменяется со временем гармонически с частотой
– начальная фаза колебаний. Таким образом, заряд на обкладках конденсатора изменяется со временем гармонически с частотой 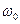 . При этом частота колебаний
. При этом частота колебаний 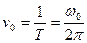 . Сила тока опережает по фазе напряжение и заряд на конденсаторе на
. Сила тока опережает по фазе напряжение и заряд на конденсаторе на 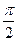 , т.е. в момент времени, когда ток достигает наибольшего значения, заряд и напряжение на конденсаторе обращаются в нуль, и наоборот. Когда конденсатор заряжен до максимальной разности потенциалов
, т.е. в момент времени, когда ток достигает наибольшего значения, заряд и напряжение на конденсаторе обращаются в нуль, и наоборот. Когда конденсатор заряжен до максимальной разности потенциалов 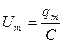 , в его электрическом поле сосредоточена энергия
, в его электрическом поле сосредоточена энергия 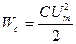 , а ток отсутствует. В момент, когда разность потенциалов и энергия электрического поля между обкладками конденсатора равны нулю, ток в контуре максимален и в магнитном поле катушки индуктивности запасена энергия
, а ток отсутствует. В момент, когда разность потенциалов и энергия электрического поля между обкладками конденсатора равны нулю, ток в контуре максимален и в магнитном поле катушки индуктивности запасена энергия 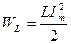 . Колебания в контуре сопровождаются взаимными превращениями энергий электрического и магнитного полей, при этом в идеальном контуре выполняется закон сохранения энергии:
. Колебания в контуре сопровождаются взаимными превращениями энергий электрического и магнитного полей, при этом в идеальном контуре выполняется закон сохранения энергии:
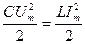 (11)
(11)
и колебания в этом случае являются незатухающими, т.е. их амплитуда не изменяется со временем. Под волновым сопротивлением контура 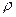 понимают индуктивное
понимают индуктивное 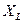 или емкостное
или емкостное 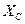 сопротивления контура, соответствующие частоте свободных колебаний, которые равны между собой:
сопротивления контура, соответствующие частоте свободных колебаний, которые равны между собой:
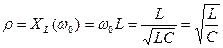 (12)
(12)
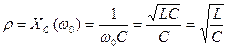 (13)
(13)
3. Затухающие колебания в контуре с активным сопротивлением.
Всякий реальный колебательный контур обладает активным сопротивлением 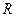 . В отсутствие внешней ЭДС (
. В отсутствие внешней ЭДС ( 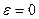 ) энергия, запасенная в контуре, постепенно расходуется в этом сопротивлении на его нагревание в соответствии с законом Джоуля-Ленца, вследствие чего колебания постепенно затухают. Уравнение, описывающее этот процесс, имеет вид (3). Это уравнение совпадает с дифференциальным уравнением затухающих механических колебаний. При условии
) энергия, запасенная в контуре, постепенно расходуется в этом сопротивлении на его нагревание в соответствии с законом Джоуля-Ленца, вследствие чего колебания постепенно затухают. Уравнение, описывающее этот процесс, имеет вид (3). Это уравнение совпадает с дифференциальным уравнением затухающих механических колебаний. При условии 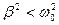 , т.е.
, т.е. 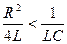 решение уравнения (3) имеет вид:
решение уравнения (3) имеет вид:
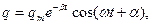 (14)
(14)
где 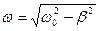 – частота собственных затухающих колебаний, которая меньше собственной частоты колебательного контура
– частота собственных затухающих колебаний, которая меньше собственной частоты колебательного контура 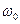 . Для напряжения на конденсаторе
. Для напряжения на конденсаторе 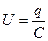 , соответственно, имеем:
, соответственно, имеем:
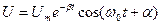 (15)
(15)
Период затухающих колебаний теперь равен:
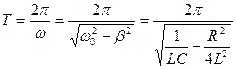 (16)
(16)
За время 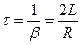 амплитуда колебаний уменьшается в
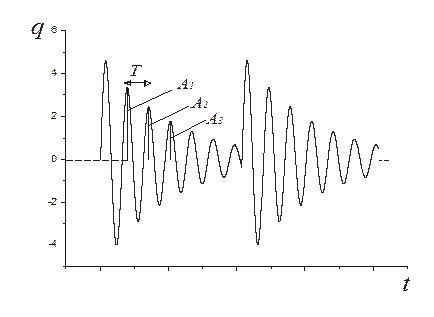
амплитуда колебаний уменьшается в 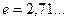 раз. Таким образом, при наличии в контуре активного сопротивления также имеет место колебательный процесс, однако частота колебаний отличается от частоты свободных колебаний и амплитуда колебаний экспоненциально убывает со временем. График изменения заряда со временем в этом случае (при периодическом воздействии внешнего источника возбуждения) изображен на рис. 2.
раз. Таким образом, при наличии в контуре активного сопротивления также имеет место колебательный процесс, однако частота колебаний отличается от частоты свободных колебаний и амплитуда колебаний экспоненциально убывает со временем. График изменения заряда со временем в этом случае (при периодическом воздействии внешнего источника возбуждения) изображен на рис. 2.
 | |||
|
Графики для силы тока и напряжения имеют аналогичный вид. Следует отметить что решение (14) уравнения (3) не является строго периодической функцией, т.к. 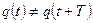 . Говорить о периоде этой функции можно лишь в том смысле, что она принимает нулевые значения через равные промежутки времени. Быстрота убывания амплитуды колебаний определяется параметром
. Говорить о периоде этой функции можно лишь в том смысле, что она принимает нулевые значения через равные промежутки времени. Быстрота убывания амплитуды колебаний определяется параметром 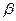 , который пропорционален отношению активного сопротивления контура к его индуктивности. На практике же обычно пользуются другими параметрами, связанными с
, который пропорционален отношению активного сопротивления контура к его индуктивности. На практике же обычно пользуются другими параметрами, связанными с 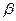 : декрементом затухания
: декрементом затухания 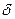 , логарифмическим декрементом затухания
, логарифмическим декрементом затухания 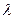 и добротностью контура
и добротностью контура 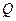 .
.
Декрементом затухания 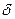 называют отношение амплитуды колебания в некоторый момент времени к амплитуде колебаний через период:
называют отношение амплитуды колебания в некоторый момент времени к амплитуде колебаний через период:
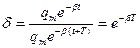 (17)
(17)
Логарифмический декремент затухания 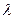 – это натуральный логарифм от декремента затухания
– это натуральный логарифм от декремента затухания 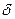 :
:
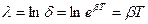 (18)
(18)
Логарифмический декремент затухания связан с числом полных колебаний Nе, совершаемых за время t, зависимостью:
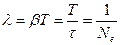 (19)
(19)
Добротность контура определяется через логарифмический декремент затухания 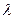 следующим образом:
следующим образом:
(20)
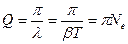 (20)
(20)
Из приведенных определений видно, что чем меньше логарифмический декремент затухания, тем выше добротность контура и тем дольше продолжается в таком контуре колебательный процесс при однократном его возбуждении. При выполнении условия 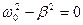 решение (3) для заряда
решение (3) для заряда 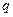 имеет вид:
имеет вид:
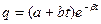 (21)
(21)
где 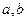 -постоянные интегрирования. При любых
-постоянные интегрирования. При любых 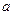 и
и 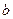 величина
величина 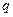 асимптотически приближается к нулю, когда
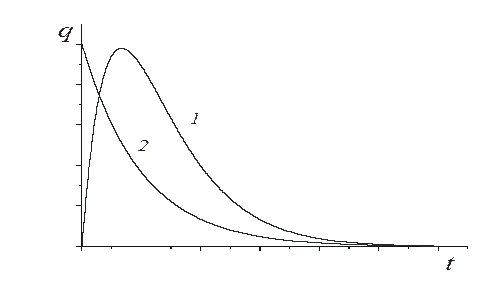
асимптотически приближается к нулю, когда 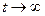 . На рис.3 представлены два частных случая апериодического процесса при
. На рис.3 представлены два частных случая апериодического процесса при 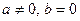 (кривая 2) и при
(кривая 2) и при 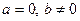 (кривая 1). В этом случае процесс не будет колебательным, а является апериодическим (рис.3). Сопротивление
(кривая 1). В этом случае процесс не будет колебательным, а является апериодическим (рис.3). Сопротивление 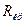 , при котором
, при котором
 | |||
|
колебательный процесс в контуре переходит в апериодический, называется критическим и определяется из условия 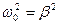 , откуда
, откуда 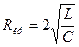 . При
. При 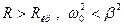 – апериодический характер процессов в колебательном контуре сохраняется.
– апериодический характер процессов в колебательном контуре сохраняется.
4. Задания и порядок выполнения работы.
1. Изучите электрическую схему лабораторной установки. Включите лабораторный стенд и получите на экране осциллографа устойчивую картину затухающих колебаний (рис.2).
2. Измерьте период затухающих колебаний 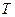 (см. рис.2). Для этого определите расстояние вдоль оси абсцисс между двумя соседними максимумами на экране осциллографа в делениях сетки экрана и умножьте полученный результат на коэффициент развертки по времени (определяется по положению ручки управления разверткой). Запишите полученный результат в таблицу (примерный вид таблицы приведен ниже).
(см. рис.2). Для этого определите расстояние вдоль оси абсцисс между двумя соседними максимумами на экране осциллографа в делениях сетки экрана и умножьте полученный результат на коэффициент развертки по времени (определяется по положению ручки управления разверткой). Запишите полученный результат в таблицу (примерный вид таблицы приведен ниже).
3. Измерьте в делениях сетки осциллографа амплитуды 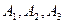 затухающих колебаний и запишите результаты измерений в таблицу. По формулам
затухающих колебаний и запишите результаты измерений в таблицу. По формулам 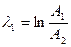 и
и 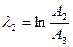 рассчитайте логарифмические декременты затухания
рассчитайте логарифмические декременты затухания 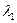 и
и 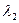 , найдите среднее значение
, найдите среднее значение 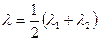 и запишите его в таблицу. Используя полученные значения
и запишите его в таблицу. Используя полученные значения 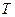 и
и 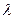 , по формуле
, по формуле 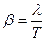 рассчитайте коэффициент затухания
рассчитайте коэффициент затухания 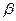 и занесите его в таблицу.
и занесите его в таблицу.
4. Пункты 2 и 3 выполняются при двух значениях 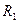 и
и 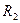 сопротивления контура. Зарисовать наблюдаемые на осциллографе кривые.
сопротивления контура. Зарисовать наблюдаемые на осциллографе кривые.
5. Подобрать значение емкости переменного конденсатора С, при котором происходит апериодический разряд конденсатора. Зарисовать получаемую кривую.
Таблица.
| T | A1 | A2 | A3 | 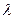 | 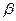 | |
| R1 | ||||||
| R2 |
Контрольные вопросы
1. Что такое колебания? Какие параметры колебательного процесса Вы знаете?
2. Что называется колебательным контуром? Как зависит собственная частота контура от его параметров?
3. Какие колебания называют свободными?
4. Что называют волновым сопротивлением и добротностью контура?
5. В чем физическая причина затухания колебаний в контуре с активным сопротивлением?
Литература
