Тема: Электрический и тепловой расчет кабеля

Цель: Изучение методики электрического и теплового расчета изоляции кабельных линий электропередач.

Знания и умения, приобретаемые студентом при выполнении практического занятия: порядок электрического и теплового расчета кабельной изоляции, навык практического проведения расчета кабельной изоляции.

В результате выполнения практического занятия у студента формируются компетенции ПК-3 (способностью принимать участие в проектировании объектов профессиональной деятельности в соответствии с техническим заданием и нормативно-технической документацией, соблюдая различные технические, энергоэффективные и экологические требования).

Актуальность практического занятия обусловлена необходимостью студентов обладать навыками электрического и теплового расчета кабельных линий.

Теоретическая часть

В общем случае при переменном токе должны рассматриваться электромагнитные процессы в изоляции кабеля. Из курса ТОЭ известно, что если длина электромагнитной волны в изоляции значительно больше диаметра кабеля, то электрическое и магнитное поля можно рассматривать отдельно. При этом для потенциала электрического поля в изоляции U применимо уравнение Пуассона

(8.1)

где Q — заряд единицы объема изоляции;

ε₀=8,85 10^-12 ф/м – диэлектрическая проницаемость вакуума;

– оператор Лапласа;

ε — относительная диэлектрическая проницаемость изоляции.

При постоянной нагрузке в кабеле имеет место стационарное тепловое поле; при этом для температуры в изоляции Т может быть записано уравнение

(8.2)

где q – выделение тепла в единицу времени в единице объема изоляции;

λ – теплопроводность изоляции.

При переменной нагрузке необходимы расчеты переходных тепловых процессов в кабеле, для которых справедливо уравнение

(8.3)

где а=λ/Сγ; С – теплоемкость и γ – плотность диэлектрика. При расчете электрического и теплового полей в кабеле находят применение в основном три указанных уравнения, которые справедливы при постоянных значениях ε, λ, γ, С.

Если в диэлектрике не имеется объемных зарядов и не выделяется тепло, то для электрического и теплового полей будут справедливы уравнения Лапласа:

и (8.4)

Как правило, температуру оболочки можно считать постоянной во всех точках. В этом случае при заданных потенциале или температуре жилы и оболочки получим одинаковую картину электрического и теплового полей. Поэтому при тепловом расчете можно использовать решения, найденные для электрического поля.

Решая приведенные выше уравнения, получим:

(8.5)

Полученное уравнение справедливо лишь при постоянных электрических параметрах среды. Если среда неоднородна, то для простейшего случая радиального поля можно не решать общие сложные уравнения, а получить расчетные формулы более простым способом, который приводится ниже.

Для переменного тока промышленной частоты выражение имеет вид:

(8.6)

где D – электрическое смещение

Для постоянного тока:

(8.7)

где j – плотность тока в изоляции.

Для плотности теплового потока можно записать

(8.8)

где превышение температуры в изоляции над температурой оболочки τ=T-T_об

T_об – температура оболочки;

q – тепловой поток через единицу поверхности в единицу времени.

Очевидна аналогия D~j~q и ~j~λ

U~T (8.9)

Соответственно для уравнений (8.6)-(8.9) можно записать интегральные соотношения:

(8.10)

(8.11)

(8.12)

где Q — заряд;

I — общий ток утечки из жилы через изоляцию;

P_ж = Qt — потери энергии в жиле.

Все величины относятся к единице длины кабеля.

Уравнения для всех трех полей одинаковы, поэтому с учетом аналогии (4.9) достаточно привести решение дли одного из этих случаев.

Проинтегрируем уравнение (8.10) и подставим в качестве пределов радиусы по жиле и изоляции. Получим соотношение между зарядом на жиле и ее потенциалом;

(8.13)

Подставив значение Q из уравнения (8.10) в (8.13), получим:

(8.14)

и для емкости кабеля

(8.15)

При ε = const емкость единицы длины кабеля вычисляется по формуле

(8.16)

Проинтегрировав (8.11), аналогичным образом получим формулы для постоянного тока;

(8.17)

(8.18)

а при γ = const сопротивление изоляции на единице длины кабеля

(8.19)

Для теплового поля из уравнения (8.12) при λ = const можно записать:

(8.20)

где τ_ж — превышение температуры жилы над температурой оболочки. В соответствии с уравнением (8.20) можно ввести понятие о тепловом законе Ома:

(8.21)

где τ_ж соответствует напряжению, — току и S_из — сопротивлению, причем из уравнения (8.21) следует, что тепловое сопротивление единицы длины кабеля

(8.22)

Из уравнений (8.12) и (8.21) можно получить зависимость превышения температуры в изоляции от радиуса кабеля:

(8.23)

Таким образом, к аналогии (8.9) после сравнения уравнений (8.19), (8.20) и (8.22) можно добавить аналогию

(8.24)

Величину 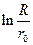— можно рассматривать как геометрический коэффициент (фактор) G, который зависит только от конфигурации электродов.

Из теории поля известно, что если поле подчиняется уравнению Лапласа, то при любой конфигурации электродов для однородной среды геометрический коэффициент будет одинаковым для электрического поля смещения, проводимости, а также для теплового поля. При этом достаточно знать одну из величин аналогии (8.24), чтобы рассчитать обе другие.

Если изоляционная среда неоднородна, то геометрический фактор будет одинаковым при условии, что зависимость параметров среды от радиуса будет одинаковой.

В соответствии с уравнением (8.5) в однородной изоляции напряженность электрического поля возле жилы максимальна и убывает по направлению к оболочке. В этом случае имеет место неполное использование электрической прочности изоляции, которое может быть количественно оценено коэффициентом использования изоляции:

(8.25)

где N=R/r₀

Е_cр — средняя напряженность поля в кабеле, которая имела бы место в конденсаторе с плоскопараллельными электродами и толщиной изоляции Δ, равной R – r₀. В большинстве случаев толщина изоляции кабеля определяется максимально допустимой рабочей напряженностью Е_р. При этом величина N может быть определена по формуле, которая следует из уравнения (8.5):

(8.26)

Из уравнений (8.14) и (8.17) следует, что при соотношении εr = const (переменное напряжение) или γr= — const (постоянное напряжение) напряженность поля будет постоянной и равной . При этом толщина изоляции будет минимальной, а коэффициент использования равен 1.

Практически при переменном напряжении уменьшение величины ε с увеличением радиуса производится ступенями. Такая изоляция называется градированной.

Если мы имеем слоистую изоляцию (рисунок 8.1), а величина ε каждого слоя составляет ε₁, ε₂, ε₃ и т. д., то из уравнения (48.14) можно получить зависимость напряженности поля от радиуса:

(8.27)

и соответственно емкость

(8.28)

Будем исходить из условия равнопрочности каждого слоя, причем электрическую прочность будем определять максимальной напряженностью поля, которая имеет место в начале слоя.

Примем допустимые (расчетные) максимальные напряженности каждого слоя E_1p, E_2p, E_3p..., E_np и введем обозначения:

и (8.29)

Тогда из уравнения (8.29) можно получить:

или и (8.30)

Рисунок 8.1 – Расположение слоев изоляции при градировании.

При этом на границе и в начале каждого слоя будем иметь расчетную напряженность поля, соответствующую этому слою.

После подстановки соотношений (8.30) в уравнение (8.27) и алгебраических преобразований можно получить:

(8.31)

Очевидно, что градирование имеет смысл лишь при

и (8.32)

что следует из соотношений (4.30).

Многослойное градирование с изменением диэлектрической проницаемости возможно для кабелей с резиновой и пластмассовой изоляцией.

В отечественной практике кабели с бумажной изоляцией градируются в два слоя, так как диапазон плотности бумаги лежит в пределах 1,2 – 0,85 г/см³, а допуск на плотность бумаги составляет 0,05 г/см³. При этом ε пропитанной бумаги составляет 4,3 при наибольшей плотности и 3,5 при наименьшей.

При двухслойном градировании

и (8.33)

При расчете изоляции кабеля необходимо учитывать, что кабельные линии во время эксплуатации, помимо длительно приложенного рабочего напряжения, подвергаются воздействию внутренних и атмосферных перенапряжений, величина и длительность которых определяются параметрами сети и установленной аппаратуры.

Необходимо учитывать также неоднородность изоляции по длине кабеля за счет различного взаимного расположения зазоров между бумажными лентами и наличия морщин, вмятин и других дефектов. В связи с этим для выбора изоляции целесообразно установить два расчетных напряжения: промышленной частоты и импульсное. Конструирование изоляции должно производиться с учетом обоих видов напряжений.

Учет различных факторов, определяющих расчетные напряжения, удобно производить в виде соответствующих коэффициентов. Расчетные напряжения промышленной частоты могут быть выбраны по формуле

(8.34)

где U_H – номинальное линейное напряжение системы.

Коэффициент k₁учитывает наибольшее возможное повышение рабочего напряжения и обычно принимается равным 1,16.

Коэффициент k₂ учитывает возможные отклонения фактической пробивной прочности изоляции от среднего значения, принимаемого при конструировании изоляции. Практически расположение зазоров между бумажными лентами распределяется по статистической закономерности. Теоретически пробивное напряжение изоляции кабелей может изменяться в пределах 15–20%. Кроме того, наличие вмятин, морщин и других дефектов может снизить электрическую прочность примерно на 10–25% в зависимости от совершенства технологии изготовления кабеля. Поэтому коэффициент k₂ выбирается в пределах 1,25—1,50.

Коэффициент k₃ учитывает уровень внутренних перенапряжений, воздействующих на кабельную линию. Опыт эксплуатации кабельных линий показывает, что максимальные перенапряжения в сетях напряжением 110 кВдостигают 3,1 U_Ф и постепенно уменьшаются с повышением напряжения до 2,25 U_Ф в сетях напряжением 500 кВ. В большинстве случаев перенапряжения имеют кратность 2,50–2,25. Учитывая, что максимальные перенапряжения имеют место весьма редко, коэффициент k₃ может быть принят равным 2,25 для линий напряжением 500 кВи 2,50 для линий напряжением 110 кВ.

Коэффициент k₄ учитывает уменьшение пробивного напряжения при снижении давления масла от расчетной величины до минимально допустимого значения, определяемого аппаратурой подпитки линии. Он обычно находится в пределах 1,10–1,20.

Таким образом, общий коэффициент запаса составляет 3,3—5,0, причем меньшее значение выбирается при надежной защите сети от перенапряжений, использовании наиболее качественных материалов и высокой культуре производства.

Таблица 8.1 – Испытательные импульсные напряжения.

Номинальное напряжение, кВ	Наибольшее рабочее линейное напряжение, кВдейств	Uисп по МЭК, кВ
минимальное	нормальное	облегченное
				–

Выбор величины расчетного импульсного напряжения может быть произведен по формуле

(8.35)

где U_исп — испытательное импульсное напряжение, соответствующее уровню импульсной прочности по рекомендации Международной электротехнической комиссии (МЭК). Величина U_исп приведена в таблице 8.1.

Минимальное испытательное напряжение рекомендуется для кабелей не имеющих непосредственного элекрического соединения с воздушными линиями передач, а облегченное – для кабелей, имеющих непосредственное соединение с воздушной линией передач в системах с надежно заземленной нейтралью.

Таблица 8.2 – Длительно допустимые температуры изоляции кабелей.

Тип кабеля	номинальное напряжение, кВ	Допустимая температура кабеля, °С
длительно	кратковременно (не более 100 ч в общей сложности)
Маслонаполенные
В стальных трубах с маслом под давлением
Газонаполненные		– –	– –
С изоляцией из сшитого полиэтилена	10-500		При протекании токов КЗ – до 250

Коэффициент k_имп учитывает неоднородность изоляции и снижение пробивной прочности с увеличением числа импульсов. Величина k_имп выбирается в пределах от 1,10-1,30.

Вопрос о предельно допустимой температуре кабеля имеет большое значение, так как от нее зависят срок службы кабеля и надежность его работы. При нагревании кабеля наиболее быстрому старению подвергается изоляция, механическая прочность и эластичность которой при этом понижаются. Значения длительно допустимых температур в кабелях, принятые в различных странах, приведены в таблице 8.2.

Основной целью теплового расчета является определение величины допустимого тока, при котором наибольшая температура в кабеле не превысит установленного значения

При включении постоянной нагрузки температура кабеля постепенно нарастает (неустановившийся режим) и после определенного промежутка времени принимает постоянное значение.

Практически наибольшая температура всегда соответствует жилам кабеля и слоям изоляции, непосредственно прилегающим к жилам. Поэтому тепловой расчет кабеля прежде всего сводится к определению температуры токоведущей жилы.

Ранее было введено понятие о тепловом сопротивлении кабеля (уравнение (8.22)). Аналогично можно рассматривать и тепловое сопротивление среды, окружающей кабель, S₀. Тогда температура жилы без учета потерь в диэлектрике может быть выражена упрощенной формулой

(8.36)

где Т₀ — температура окружающей среды;

∑Р_К — суммарные потери в кабеле; S_n — тепловое сопротивление защитных покровов; S₀ – тепловое сопротивление окружающей среды.

Таким образом, для теплового расчета необходимо произвести следующие вычисления:

1.Определение потерь в жиле Р_ж, оболочках Р_об и изоляции (диэлектрические потери) P_д кабеля.

2. Определение тепловых сопротивлений:

а) изоляции кабеля и его защитных покровов;

б) среды, окружающей кабель.

Кроме того, необходимо учесть колебания температуры окружающей среды Т₀ за счет сезонных изменений температуры и посторонних источников тепла. Потери в токопроводящей жиле на единице длины кабеля при постоянном токе вычисляются по формуле

(8.37)

(8.38)

где I —ток в жиле, А; q – сечение жилы, м²

ρ_о – удельное электрическое сопротивление жилы при 20° С; α — температурный коэффициент увеличения сопротивления меди и алюминия (0,004 град^-1); k₀ – коэффициент, учитывающий удлиннение жил при скручивании, который может быть взят из таблицы 4.3.

Таблица 8.3 – Значения коэффициента k₀ для различных конструкций кабелей

Конструкция кабеля	k0
Одножильные кабели с сечением жилы менее 500 мм2	0,03
Одножильные кабели с сечением жилы 500—1000 мм2	0,04
Одножильные кабели с сечением жилы свыше 1000 мм2	0,05
Многожильные кабели (независимо от сечения жилы) .	0,04

Потери при переменном токе вычисляются по формуле

(8.37)

(8.38)

где коэффициенты вычисляются по следующим формулам:

(8.39)

(8.40)

(8.41)

(8.42)

f – частота сети, Гц, d_Ж – наружный диаметр жилы кабеля, S – расстояние между центрами жил кабеля, k – коэффициент, зависящий от конструкции кабеля (таблица 8.4). При этом для расчета y_П по формулам (8.39-8.40) берется коэффициент из столбца поверхностный эффект, а при расчете коэффициента y_Б берется коэффициент из столбца эффект близости. Формула (8.41) используется для двухжильных кабелей или двух рядом расположенных кабелей, а (8.42) – для трехжильных и трех рядом расположенных кабелей. При прокладке кабеля в стальной трубе используется формула:

(8.43)

Таблица 8.4 – Значения коэффициента k для различных конструкций жил

Тип жилы	Поверхностный эффект	Эффект близости
Круглая, скрученная (уплотненная и неуплотиеиная)		0,8
Круглая, состоящая из четырех изолированных друг от друга секторов или сегментов ( c центральным каналом или без него)	0,435	0,37
Полая		0,8
Секторной формы		0,8

Потери в проводящих оболочках кабеля состоят из потерь на вихревые токи, при расчете данными видами потерь, как правило, пренебрегают, и потерь на продольные токи, которые можно оценить по следующим формулам:

а) для трех кабелей, проложенных по вершинам треугольника

(8.44)

где R_ОБ=ρ_ОБ/π(r_ОБ.Н-r_ОБ.В)², ρ_ОБ – удельное сопротивление материала оболочки, r_ОБ.Н – наружный радиус оболочки, r_ОБ.В – внутренний радиус оболочки; ; ω – круговая частота тока в кабеле.

б) для кабелей, расположенных в одной плоскости:

(8.45)

(8.46)

(8.47)

(8.48)

(8.49)

Для среднего кабеля используется формула (8.45), для крайних кабелей – формула (8.46).

Расчет теплового сопротивления изоляции одножильного кабеля без учета диэлектрических потерь может быть проведен по следующей форме:

(4.50)

где σ_из— удельное тепловое сопротивление изоляции, °С∙м/вт.

Расчет теплового сопротивления защитных покровов производится по такой же формуле, но под знак логарифма необходимо подставлять отношение радиуса с защитными покровами к радиусу без защитных покровов.

Таблица 8.5 – Удельные тепловые сопротивления различных материалов

Материал	σиз, °С∙м/вт	Теплоем­кость С, ккал/кг∙°С	Плотность, г/см
Бумажная изоляция с вязкой пропиткой	В состоянии поставки	1 – 10 кВ 20 и 35 кВ	5-6,5 5-5,5	0,33 0,33	1,252 1,252
В нормальной эксплуатации	1 –10 кВ 20 и 35 кВ	6-7 5,5-6	0,33 0,33	1,252 1,252
Газонаполненный, обедненная пропитка	6,5-7
Бумажная изоляция маслонаполненных кабелей	4,5-5	0.33	1,252-1,365
Полиэтилен	3-4	0,55	0,95
Полихлорвиниловыи пластикат	6-7	0,32	1,25
Резина	5-7	0,33—0,4	1,4
Кабельная пряжа	5,5-6	–	–
То же с ленточной броней		–	–
Медь	0,0027	0,091	8,89
Алюминии	0,0048	0,22	2,7
Свинец	0,029	0,031	11,34
Сталь	0,014-0,012	0,11	7,8
Минеральное масло		0,40	0,9
Почва с повышенной влажностью: песок >9%, песчано-глинистая >14%	0,8	До 0,50	2,80—2,0
Почва с нормальной влажностью: песок 7—9%, песчано-глинистая 12—14%	1,2	0,20	1.9
Почва с пониженной влажностью: песок 4—7°/о, песчано-глинистая 8—12%	1,8	0,20	1,8
Сухая почва: Песок 4% влаги. Каменистая почва	2,4	0,19	1,43
Бетон	0,9	0,20	2.2
Асфальт	1,6	0,40	1,0

Величины удельных тепловых сопротивлений различных материалов приведены в таблице 8.5. Тепловые потери в диэлектрике в отличие от потерь в жиле распределены по всей изоляции кабеля, поэтому расчет превышения температуры жилы кабеля за счет диэлектрических потерь будет несколько иным.

При наличии потерь в жиле и изоляции перепад температур между жилой и оболочкой можно вычислять по формуле

(8.51)

При определении температуры кабелей диэлектрические потери в изоляции учитываются только в кабелях на напряжение 100 кВи выше, так как в современных кабелях на меньшее напряжение диэлектрические потери весьма малы по сравнению с потерями в меди.

Определение теплового сопротивления окружающей среды.

Кабель, проложенный в воздухе, охлаждается путем переноса тепла от наружной поверхности к окружающему воздуху путем конвекции. Наряду с этим некоторое значение имеет и передача тепла посредством теплового излучения.

Охлаждение кабеля может быть различным в зависимости от скорости и направления перемещения воздуха (обдувания). На практике для расчетов обычно принимают среднее значение коэффициента теплопередачи для свободной конвекции.

При прокладке в туннелях и каналах следует учитывать общий нагрев воздуха в туннеле, наличие горячих восходящих потоков воздуха от расположенных ниже кабелей и нагретых труб.

Как правило, воздушное охлаждение менее эффективно, чем охлаждение при прокладке в земле, за исключением некоторых случаев, когда прокладка ка белей производится на большой глубине. На кабели напряжением до 10 кВнагрузка в воздухе обычно снижается по сравнению с нагрузкой в земле примерно на 20—30%.

При прокладке в воздухе превышение температуры поверхности кабеля над температурой окружающего воздуха может быть вычислено по формуле

(8.52)

где ∑р — сумма всех потерь в кабеле;

S_B — сопротивление теплопередачи к воздуху.

Сопротивление теплопередачи от поверхности кабеля в воздух зависит от диаметра кабеля, состояния его поверхности, разности температур между кабелем и воздухом и средней температуры воздуха. Расчет конвективной теплопередачи может быть произведен по критериальным уравнениям теории теплопередачи.

На практике пользуются обычно упрощенными формулами. Простейшая эмпирическая формула для расчета сопротивления теплоперехода в воздух имеет вид:

(8.53)

где A – удельное сопротивление теплопереходу от поверхности кабеля в воздух, град∙см²/втвыбирается по табл. 4.6; D_H — наружный диаметр кабеля, см.

Таблица 8.6 – Зависимость удельного сопротивления теплоперехода воздух-кабель.

Диаметр кабеля, см	2,5	5,0	7,5	10,0	22,0
Величина А, град∙см2/вт	Кабель слабо нагружен
Кабель сильно нагружен

При прокладке кабеля в земле поверхности грунта и кабеля можно приближенно принять за изотермические. Тогда, пользуясь методом зеркальных отображений для однородного грунта, по аналогии с электрическим полем можно получить формулу для теплового сопротивления земли:

(8.54)

(8.55)

(8.56)

где σ_З — удельное тепловое сопротивление земли, окружающей кабель, град∙см²/вт; D_H — наружный диаметр кабеля, м, L – глубина прокладки кабеля, м.

Формула (8.54) используется для одиночного кабеля, (8.55) – для трех кабелей, расположенных по треугольнику, (8.56) – для трех кабелей, расположенных в одной плоскости.

При постоянной температуре поверхности грунта в установившемся режиме тепло будет отводиться только к поверхности грунта.

Удельное тепловое сопротивление грунта сильно зависит от структуры почвы и содержания в ней влаги, как это видно из таблицы 4.5.

Для расчета допустимого тока нагрузки в жиле необходимо построить схему замещения тепловых сопротивлений и потоков для рассматриваемой конкретной конструкции кабеля и условий прокладки.

Для одножильного кабеля, проложенного в воздухе, в соответствии с тепловым законом Ома можно записать:

(8.57)

Если подставить в уравнение (8.57) значение потерь, то для допустимого тока нагрузки получим:

(8.58)

где T_макс – максимально допустимая температура жилы, выбираемая по таблице 8.2.

Задания

1. Рассчитать радиус по изоляции кабеля и радиус первого слоя изоляции кабеля, если последняя состоит из двух слоев. Для первого слоя ε₁=4,3; E_1p=12,5 кв/мм. Для второго слоя ε₂=3,5; E_2p=11,8 кв/мм. Радиус жилы r₀=12,2 мм. Напряжение линии U = 220 кВ.

Решение.

Рассчитываем предварительно величины: и f= E_1P/E_2P=1.064

Затем определяем расчетные напряжения:

кВ (8.59)

кВ (8.60)

Так как импульсная прочность бумажно-масляной изоляции намного больше, чем прочность при напряжении промышленной частоты, то выбираем в качестве расчетного напряжение промышленной частоты.

Далее по формуле (4.33) получим

мм и мм (8.61)

Толщина изоляции Δ=R-r₀ = 179,1 мм.

Следует отметить, что при градировании наибольший эффект достигается при большой величине соотношения радиусов R/r₀, так как при малом соотношении радиусов неравномерность поля невелика и выравнивание поля при градировании лишь незначительно сказывается на уменьшении толщины изоляции.

2. Рассчитать изоляцию маслонаполненного кабеля высокого давлениянапряжением U=220 кВ. Радиус жилы r₀= 12,2 мм, диаметр канала 10 мм.

Решение.

Для выполнения изоляции кабеля выбираем бумагу толщиной 0.075 (γ=1,1-1,2); 0,125 мм(γ=0,85-0,9).. Данные о свойствах выбранной бумаги введены в таблице 4.7.

Таблица 8.7 – Данные для расчета

№ слоя	Толщина бумаги	Плотность бумаги г/см3	ε	Прочность при переменном напряжении промышленной частоты, кВ/мм	Прочность при импульсном напряжении, кВ/мм			k=ε1/ε2
	0,075	1,1–1,2	4,3
	0,125	0,85–0,90	3,5			1,061	1,11	1,23

Расчетные напряжения выбираем аналогично с задачей 4.1

По формуле (4.33) находится соотношение радиусов.

При промышленной частоте

(8.62)

При импульсном напряжении

(8.63)

Из двух вычисленных значений N выбирается большее (N₂=2,18). Таким образом, толщину изоляции кабеля будет в данном случае определять импульсное напряжение.

При низком и среднем давлениях толщину изоляции, как правило, определяет напряжение промышленной частоты.

Находим радиус R=N₂r₀=26.6мм; Толщина изоляции Δ_из =R-r₀=14.4мм.

Радиус r₁ начиная с которого необходимо производить наложение бумаги с меньшей диэлектрической проницаемостью (0,125 мм), определяется по формуле (8.33): r₁=kf₁r₀=16.6 мм.

Толщина слоя уплотненной бумаги (0,075 мм)составит Δ_из =r₁-r₀=4.4 мм.Далее необходимо проверить величину напряженности поля во втором (при r=r₁) слое при расчетном напряжении U₁=508 кВ. Формулы (8.63) выведены из условия наличия слоев заданной напряженности на границе. Поэтому при напряжении U₂ = 1080 кВнапряженность электрического поля составит: при r= r₀ кВ/мм; при r= r₁ кВ/мм.

Очевидно, что при напряжении U₁ — 508 кВнапряженность уменьшится в 2,12 раз. Тогда для U₁напряженность поля составит: при при r= r₀ кВ/мм; при r= r₁ кВ/мм

Таким образом, напряженность поля при расчетном напряжении промышленной частоты не превышает пробивной напряженности (таблица 8.7) для всех слоев.

3. Провести расчет допустимого тока группы из трех кабелей из задачи 2, проложенных по вершинам треугольника, глубина прокладки кабелей в земле 1,5 м. кабели выполненными бронированными, толщина брони 1 мм, толщина свинцовой оболочки 3 мм, толщина защитных покровов 5 мм.

Решение

Зададимся значениями температуры окружающей среды T₀=20°C, максимально допустимой температуры жилы кабеля по таблице 4.2 T_макс=60°C.

Затем рассчитаем сопротивление жилы кабеля:

, Ом (8.64)

Где; q=π(r₀-r_k)²=1,63·10^-4, м²; ρ_о=0,027·10^-6 Ом·м; α=0,004; k₀=0,03

Ом (8.65)

где коэффициенты вычисляются по следующим формулам:

(8.66)

(8.67)

Для расчета коэффициента y_Б

(8.68)

(8.69)

(8.70)

f =50 Гц, d_Ж=24,4 мм, S=,

Далее вычисляем потери в защитных оболочках кабеля:

а) для свинцовой оболочки

(8.71)

где R_ОБ=ρ_ОБ/π(r_ОБ.Н)²-(r_ОБ.В)²=4,04·10^-4 Ом, ρ_ОБ = 0,214·10^-6 Ом·м, r_ОБ.Н=29,6 мм, r_ОБ.В=26,6 мм; =1.62·10^-5;

б) для стальной брони

(8.72)

где R_ОБ=ρ_ОБ/π(r_ОБ.Н)²-(r_ОБ.В)²=7,3·10^-4 Ом, ρ_ОБ = 0,138·10^-6 Ом·м, r_ОБ.Н=30,6 мм, r_ОБ.В=29,6 мм; =1.18·10^-5;

Найдем суммарные потери в оболочках

(8.73)

Определим диэлектрические потери в кабеле, для этого вычислим емкость кабеля на единицу длины:

нФ/м (8.74)

Диэлектрические потери рассчитаем по формуле:

Вт/м (8.75)

Таблица 8.8 – Характеристики некоторых типов изоляции кабелей

Тип кабеля	ε	tgδ
Кабели с пропитанной бумажной изоляцией:
С вязкой пропиткой, с полностью или предварительно пропитанной изоляцией и пропитанные нестекающсй массой		0,01
Маслонаполненные низкого давления	3.3—3,75	0,004–0,0045
Маслонаполненные высокого давления в стальном трубопроводе	3,7	0,0045
газонаполненные	3.4-3,5	0,004 -0,0045
Кабели с изоляцией из других материалов:
Из резины на основе бутилкаучука	4,5	0,05
Из этиленпропиленовой резины		0,040
Из поливинилхлорида		0,1
Из термопластичного полиэтилена	2,3	0,001
Из сшитого полиэтилена	2,5	0,0008

Далее рассчитаем тепловые сопротивления элементов кабеля:

, С∙м/вт (8.76)

где σ_из=5 °С∙м/вт.

, С∙м/вт (8.76)

где σ_из=6 °С∙м/вт.

С∙м/вт (8.77)

где σ_В=0,8 °С∙м/вт.

После всего подставляем все рассчитанные значения в формулу (8.58) и вычисляем максимально допустимый ток в кабеле.

А. (8.78)

4. Провести расчет допустимого тока группы из трех кабелей на напряжение 330 кВ, проложенных по вершинам треугольника, глубина прокладки кабелей в земле 1,2 м. кабели выполненными бронированными, толщина брони 3 мм, толщина свинцовой оболочки 3 мм, толщина защитных покровов 6 мм. Изоляция – бумажно-масляная под высоким давлением.

5. Провести электрический расчет кабеля с изоляцией из сшитого полиэтилена на напряжение 35 кВ, сечением 400 мм².

Контрольные вопросы.

1. Особенности работы изоляции на постоянном напряжении.

2. Допустимые испытательные постоянные напряжения для оборудования переменного тока.

3. Контроль изоляции с применением повышенного постоянного напряжения.

4. Маркировка силовых кабелей.

5. Кабели на напряжение до 1 кВ.

6. Кабели с полиэтиленовой изоляцией.

7. Кабели с бумажно-масляной изоляцией.

8. Особенности конструкции кабелей на напряжение 35 кВ и выше.

9. Электрический расчет кабеля.

10. Последовательность теплового расчета кабеля.

Список литературы, рекомендуемый к использованию по данной теме

Основная литература

1. Электроснабжение сельского хозяйства: учебник / т. Б. Лещинская, и. В. Наумов ; [ред. Г. В. Лихачёва]. - М. : Колос, 2008. - 655 с. – ISBN 978-5-9532-0560-3.

2. Расчет электрических полей устройств высокого напряжения : учеб. пособие / И. П. Белоедова, Ю. В. Елисеев, Е. С. Колечицкий и др. ; ред. Е. С. Колечицкий. - М.: ИД МЭИ, 2008. - 248 с. – ISBN 978-5-383-00072-4

Дополнительная литература

3. Техника высоких напряжений : учебник для вузов / под ред. Д. В. Разевига. – 2-е изд., пер. и доп. – М. : Энергия, 1976. – 488 с.

4. Техника высоких напряжений(изоляция и перенапряжение в электрических установках) : учебник для техникумов / В. П. Ларионов, В. В. Базуткин, Ю. Г. Сергеев ; под ред. В. П. Ларионова. – М. : Энергоиздат, 1982. – 296 с.

5. Алиев, И. И. Электротехнические материалы и изделия: справочник / И. И. Алиев. - Изд. 2-е, испр. - М. : РадиоСофт, 2007. - 352 с. – ISBN 5-93037-133-4

Практическое занятие №5