Тема 3. Показникова форма запису комплексних чисел.
З урахуванням наведених вище співвідношень комплексне число можна представити у вигляді
.
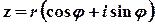Така форма запису комплексного числа називається тригонометричною, а множення, ділення та піднесення до натурального степеня виконуються за формулами
;
;
.
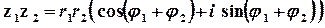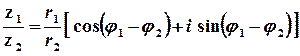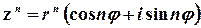З урахуванням формули Ейлера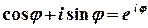 
комплексне число може бути записано у показниковій формі
.
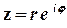Якщо комплексні числа записані у показниковій формі, то дії множення, ділення та піднесення до натурального степеня виконуються за правилами
;
;
.
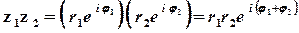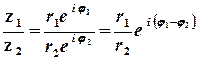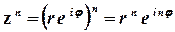Коренем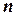 
-го степеня з комплексного числа 
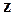називається таке число, 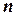-ий степінь якого дорівнює 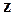. Обчислення кореня виконується за формулою
,
,
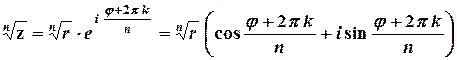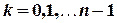тобто корінь 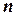-го степеня має 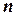значень.
ПИТАННЯ ТА ЗАВДАННЯ ДЛЯ
САМОСТІЙНО
ОПРАЦЮВАНОГО МАТЕРІАЛУ
Тема 1. Дії над комплексними числами.
Завдання для самоконтролю:
1.1 Виконати арифметичні дії з комплексними числами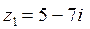 
і 
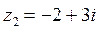
1.2 Подати вираз у вигляді двох спряжених комплексних чисел: 1)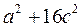 
;
2) 
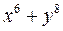; 3) 26.
1.3 Обчислити степені: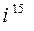 
; 
; 
; 
.
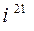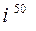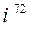Питання для самоконтролю:
1. Чи можуть сума, різниця, добуток к і частка двох комплексних чисел дорівнювати дійсному числу ?
2. Чому дорівнюють сума та добуток двох спряжених комплексних чисел ?
3. Скільки різних степенів має уявна одиниця ?
Тема 2. Геометрична інтерпретація комплексних чисел.
Завдання для самоконтролю:
2.1. Знайти геометричне зображення комплексних чисел: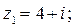 
.
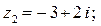
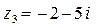2.2. Виконати додавання і віднімання комплексних чисел у геометричній формі:
а)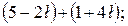 
б)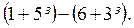 
Питання для самоконтролю:
1. В яких чвертях розміщені точки, що зображають комплексні числа: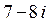 
; 
;
; 
.
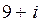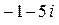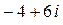2. Що можна сказати про взаємне розміщення точок, які зображують спряжені комплексні числа? протилежні комплексні числа?
3. Як можна геометрично інтерпретувати додавання і віднімання двох комплексних чисел?
Тема 3. Показникова форма запису комплексних чисел.
Завдання для самоконтролю:
3.1. Записати комплексне число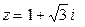 
в тригонометричній та показникові формах.
3.2. Знайти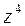 
та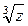 
, якщо 
.
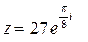Питання для самоконтролю:
1. Формули переходу від алгебраїчної форми запису комплексного числа z показникової форми.
2. Дії з комплексними числами, що задані в показникові формі ( алгебраїчна сума,
множення , ділення, піднесення до степеня і добування кореня).
ЛІТЕРАТУРА:
1. Шкіль М. І., Колесник Т. В., Котлова В.М. Вища математика. – К .:Вища школа,1984.
2. Баврин И. И. Высшая математика. – М.: Просвещение. 1986.
3. Кривуца В.Г., Барковський В.В., Барковська Н.В. Вища математика. Практикум:
Навчальний посібник. – К.: Центр навчальної літератури, 2005.
ВІДПОВІДІ ДО ЗАВДАНЬ САМОКОНТРОЛЮ:
1.1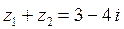 
; 
; 
; 
.
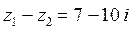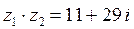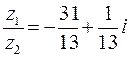1.2 1)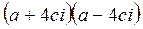 
; 2) 
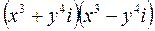; 3)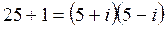 
.
1.3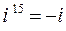 
; 
; 
; 
.
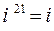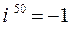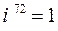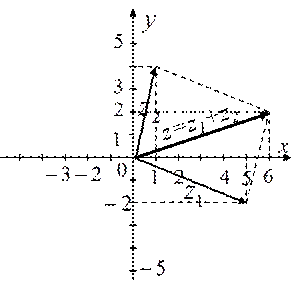2.1 2.2 а)
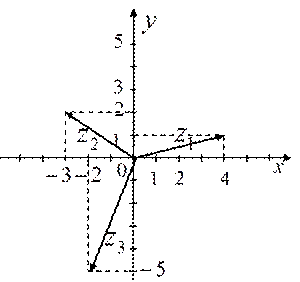
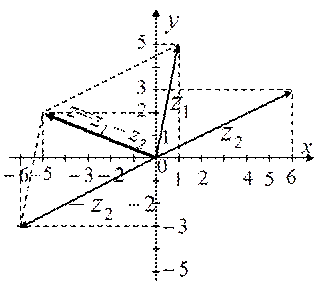
2.2 б )
3.1.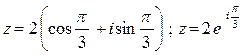 
3.2.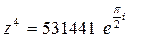 
; 
.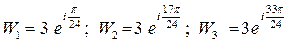