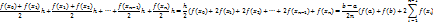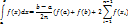Замена переменной в определенном интеграле

При вычислении определенных интегралов с использованием формулы Ньютона-Лейбница предпочтительно жестко не разграничивать этапы решения задачи (нахождение первообразной подынтегральной функции, нахождение приращения первообразной). Такой подход, использующий, в частности, формулы замены переменной и интегрирования по частям для определенного интеграла, обычно позволяет упростить запись решения.

ТЕОРЕМА. Пусть функция φ(t) имеет непрерывную производную на отрезке [α,β], а= (α), в= (β) и функция f(х) непрерывна в каждой точке х вида х= (t), где t [α,β], Тогда справедливо следующее равенство: 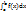= 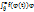’(t)dt

Эта формула носит название формулы замены переменной в определенном интеграле.

Подобно тому, как это было в случае неопределенного интеграла, использование замены переменной позволяет упростить интеграл, приблизив его к табличному (табличным). При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования α и β по новой переменной t как решение относительно переменной t уравнений φ(t)=а и φ(t)=в. На практике, выполняя замену переменной, часто начинают с того, что указывают выражение t=ψ(х) новой переменной через старую. В этом случае нахождение пределов интегрирования по переменной t упрощается: α=ψ(а), β=ψ(в).

15)Интегрирование по частям определенного интеграла:

Формула интегрирования по частям:

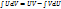
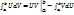
16) Вычисление площадей плоских фигур:

Площадь криволинейной трапеции в декартовых координатах:

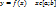
1.

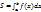
2.

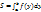
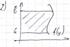
3.

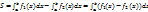
4.

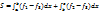
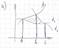
Площадь криволинейной трапеции ограниченная функциями заданными параметрически:

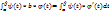
17)Площадь фигуры в полярных координатах:

Если линии заданы в полярной системе координат(уравнения таких линий имеют вид 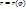или 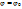, а связь полярных координат с декартовыми: 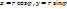, то все аналогично. При этом следует помнить, что всегда 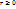, а линия 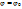представляет собой луч, выходящий из начала координат и составляющий с положительным направлением оси ОХ угол .

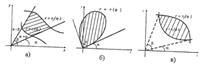
Для случаев а) и в) площадь фигуры определяется с помощью интеграла

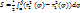
Для б) с помощью интеграла

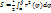
18) Длина дуги кривой:

Декартовые координаты:

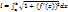
19) Длина дуги в параметрическом виде:

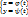
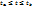
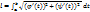
20)Длина дуги в полярных координатах:

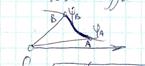
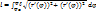
Объем теловращения.

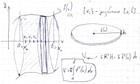
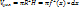
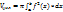
Если криволинейную трапецию ограничить сверху графиком а(ч) осью ОХ и по бокам прямым у = а и х = b, то получится тело вращения.

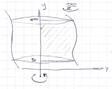
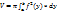
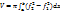
Приближенное вычисление определенных интегралов (признак сравнения).

{a;b} разбиваем на n одинаковых отрезков 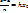,