Знакопеременные и знакочередующиеся ряды
Ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными.
Пусть дан знакопеременный ряд
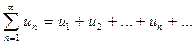 . (4)
. (4)
Рассмотрим знакоположительный ряд, состоящий из модулей членов ряда (4):
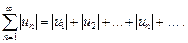 (5)
(5)
Ряд (4) сходится, если сходится ряд (5). В этом случае ряд (4) называется абсолютно сходящимся. Если же ряд (4) сходится, а ряд (5) расходится, то ряд (4) называется условно сходящимся.
Частным случаем знакопеременного ряда является знакочередующийся ряд
u1 – u2 + …+ (–1)n+1 un + … = 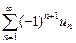 (6)
(6)
(un > 0, n = 1, 2, …),
в котором положительные и отрицательные члены следуют друг за другом поочередно.
Для знакочередующихся рядов имеет место достаточный признак сходимости.
Теорема (признак Лейбница)
Знакочередующийся ряд (6) сходится, если:
1. Последовательность абсолютных величин членов ряда монотонно убывает, т. е. 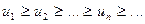 .
.
2. Общий член ряда стремится к нулю, т. е. 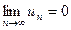 .
.
При этом остаток Rn = S – Sn не превосходит по модулю первого отбрасываемого члена 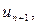 т. е.
т. е. 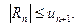
Степенные ряды
Будем рассматривать ряды, членами которых являются степенные функции:
a0 +a1 x + a2 x2 + … + an xn + … = 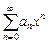 . (7)
. (7)
Такие ряды называются степенными, а числа ai (i = 0, 1, 2, …) — коэффициентами этого степенного ряда.
Множество тех значений х, при которых степенной ряд (7) сходится, называется областью сходимости этого степенного ряда.
Число R называется радиусом сходимости ряда (7), если при всех х, удовлетворяющих неравенству 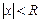 , ряд (7) сходится, а при всех x, удовлетворяющих неравенству
, ряд (7) сходится, а при всех x, удовлетворяющих неравенству 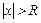 , — расходится.
, — расходится.
Радиус сходимости R определяется по формуле
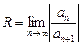 .
.
Интервал (–R; R) называется интервалом сходимости ряда (7).
При x = R, x = –R ряд (7) может как сходиться, так и расходиться. Вопрос о сходимости ряда (7) в этих точках решается путем дополнительных исследований.
Ряд Маклорена
Ряд 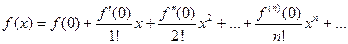 называется рядом Маклорена для функции f(x).
называется рядом Маклорена для функции f(x).
Приведем следующие известные разложения функций в ряд Маклорена:
1. 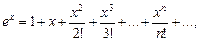 область сходимости
область сходимости 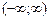 .
.
2. sinx = 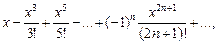 область сходимости
область сходимости 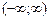 .
.
3. 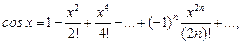 область сходимости
область сходимости 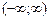 .
.
4. 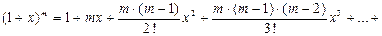
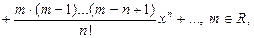 область сходимости (–1;1).
область сходимости (–1;1).
5. 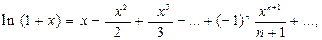 область сходимости (–1;1].
область сходимости (–1;1].
6. 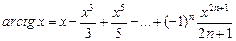 + …, область сходимости
+ …, область сходимости
[–1;1].
Вопросы для самопроверки
1. Что называется числовым рядом, членами ряда? Приведите примеры.
2. Что вы понимаете под суммой ряда? Какой ряд называется сходящимся?
3. Сформулируйте признак расходимости ряда в термине предела общего члена.
4. Дайте определение обобщенного гармонического ряда. При каких р он сходится?
5. Сформулируйте первый и второй признаки сравнения. В чем их общность и отличие?
6. Сформулируйте достаточный признак сходимости знакочередующегося ряда. Как вычислить сумму членов знакочередующегося ряда с указанной степенью точности?
7. Что называется степенным рядом? Что вы понимаете под точкой сходимости этого ряда?
8. Что называется радиусом сходимости степенного ряда и как его определить?
9. Чем отличается область сходимости от интервала сходимости степенного ряда?
10. Какие основные свойства степенных рядов вы знаете?
11. Что вы понимаете под рядом Маклорена? Как разложить функции в этот ряд?
12. Какие разложения элементарных функций в ряд Маклорена вы знаете?
Типовая задача 4
Написать степенной ряд по заданному общему члену
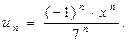
Найти область сходимости этого ряда.
Решение. При n = 0 получаем свободный член a0 = 1 данного ряда, при n = 1 — член 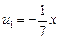 , при n = 2 — член
, при n = 2 — член 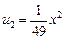 и т. д.
и т. д.
Получаем следующий ряд:
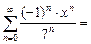
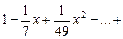
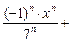 … .
… .
Находим радиус сходимости данного ряда. Имеем:
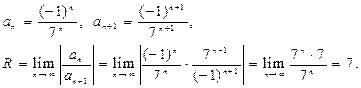
Следовательно, (–7; 7) — интервал сходимости ряда. Исследуем поведение ряда на концах интервала сходимости, т. е. при x = –7,
x = 7.
Пусть x = –7. Тогда степенной ряд принимает вид
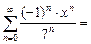
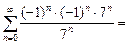
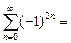 1 + 1 + …+ 1 + … .
1 + 1 + …+ 1 + … .
Так как 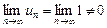 , то ряд расходится (достаточное условие расходимости числового ряда).
, то ряд расходится (достаточное условие расходимости числового ряда).
Пусть x = 7. Получаем следующий знакочередующийся ряд:
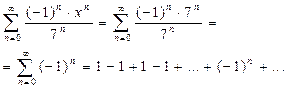
Этот ряд расходится, так как не существует предела последовательности 1,0,1,0… частичных сумм этого ряда.
Таким образом, (–7; 7) — область сходимости данного степенного ряда.
Ответ: (–7; 7).
Типовая задача 5
Вычислить определенный интеграл 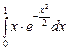 с точностью до 0,001, используя разложение подынтегральной функции в ряд Маклорена.
с точностью до 0,001, используя разложение подынтегральной функции в ряд Маклорена.
Решение. Воспользуемся разложением функции ex:
ex = 1 + x + 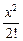 + … +
+ … + 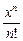 + … .
+ … .
Заменив x на 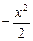 , получим:
, получим:
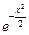 = 1 –
= 1 – 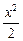 +
+ 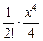 – … +
– … + 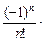
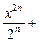 … .
… .
Умножая обе части последнего равенства на x, будем иметь:
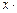
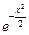 = x –
= x – 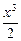 +
+ 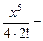 …+
…+ 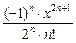 +… .
+… .
Итак, 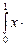
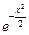 dx =
dx = 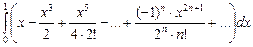 =
=
= 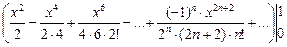 =
= 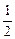 –
– 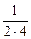 +
+ 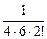 –
–
– … + 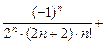 … =
… = 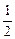 –
– 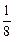 +
+ 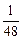 – … +
– … + 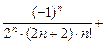 … .
… .
Получаем знакочередующийся ряд. По признаку Лейбница имеем:
1. 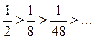 .
.
2. 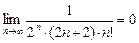 .
.
Значит, ряд сходится. По этому признаку первый отбрасываемый член по модулю меньше un+1. Если un+1 взять по модулю меньшим, чем 0,001, то из 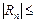 un+1 < 0,001 следует, что остаток Rn меньше 0,001. Имеем:
un+1 < 0,001 следует, что остаток Rn меньше 0,001. Имеем:
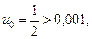
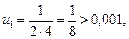
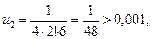
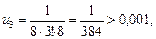
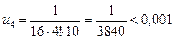 .
.
Значит, 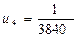 — первый отбрасываемый член.
— первый отбрасываемый член.
Таким образом, с точностью до 0,001
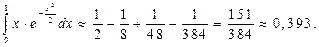
Ответ: 0,393.
4. Задания 6 и 7
по теме «Обыкновенные дифференциальные уравнения»
