Эйлер әдісін итерация әдісімен жалғастыру

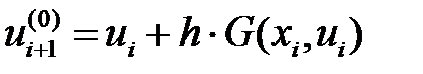. (6)

Енді итерациялық процесс құрамыз

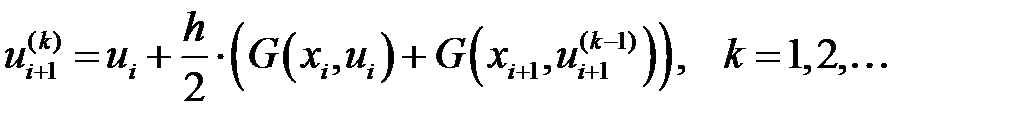(7)

Мысал. 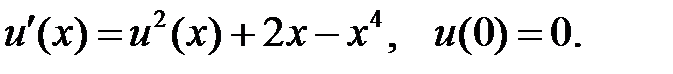Мұндағы 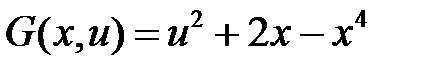. Есептің дәл шешімі 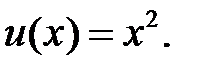Эйлер әдісі.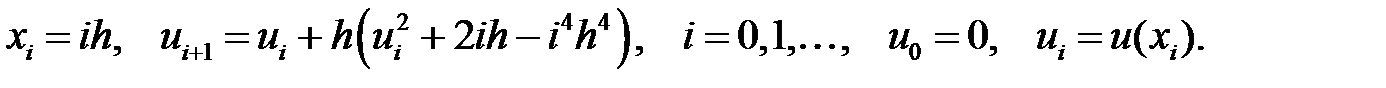

18. Қарапайым дифференциалдық операторлардың айырымдық аппроксимациясы........

Торлық ңдістер есептеу математикасында дифференциалдық тењдеулерді айырымдық тењдеулермен алмастыруѓа негізделген екенін жоѓарыда айтып кеткен болатынбыз. Сондай-ақ ол тењдеулердегі туындыларды айырымдық операторлармен жуықтау арқылы жџзеге асырылатыны жайлы да айтылѓан. Біз мынадай жай дифференциалдық операторларды ѓана қарастыратын боламыз:

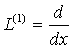жңне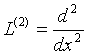

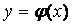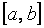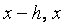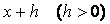1⁰.Айталық функциясы аралыѓында анықталѓан жңне қажетті (қажетінше) џзіліссіз туындылары бар функция болсын. Ал жңне осы 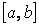аралыѓыныњ бірдей қашықтықта жатқан кљршілес нџктелері делік.

Математикалық анализ курсында 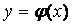функциясыныњ 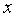нџктесіндегі 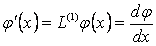туындысы тљмендегі шектер арқылы анықталѓан болатын:

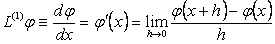(1.2.1)

немесе

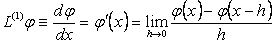(1.2.2)

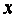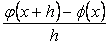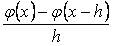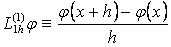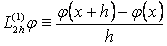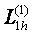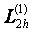Егер бекітілген сан болса, онда жңне шамаларын айырымдық қатынастар деп қарастырса да болады. Сандық ңдістер теориясында оларды айырымдық операторлар деп атап, былайша белгілейді: жңне . Кейде оларды айырымдық туындылар деп те атайды. жңне операторлардаѓы (1.2.1) белгісі олардыњ бірінші ретті 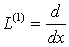туындыѓа сңйкес келетінін білдіреді.

Ал егер (1.2.1) жңне (1.2.2) тењдеулерінде 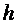-ты мейлінше аз шама деп есептеп, ондаѓы lim белгісін алып тастасақ, онда 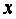нџктесінде мынадай жуық тењдіктерді алѓан болар едік:

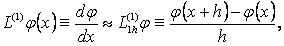
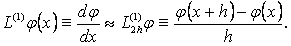
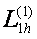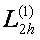Енді осы жңне операторлары арқылы орташа айырымдық туынды деп аталатын мынадай операторды қђрамыз:

.

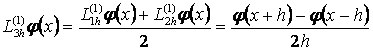Бђл жаѓдайда да 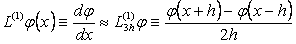деп жазуѓа болады.

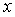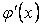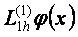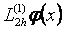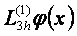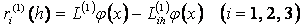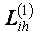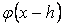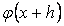Сонымен бекітілген нџктесінде туындысын , немесе мңндерімен жуықтауѓа болады деген тђжырымѓа келеміз. ңдетте айырымдарын операторыныњ жуықтау қателіктері деп атайды. Осы қателіктерді баѓалау мңселесіне тоқталайық. Ол џшін алдымен жңне шамаларын 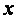нџктесініњ кіші аймаѓында Тэйлор қатарына жіктейміз:

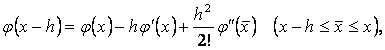
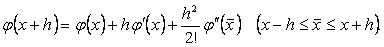
Енді осы љрнектерді пайдаланып, 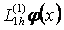жңне 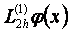-тіњ мңндерін есептейміз:

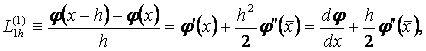
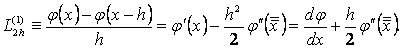
Демек,

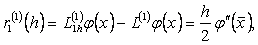
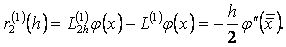
Мынадай белгілеуді енгізейік: .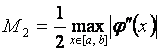

Сонда 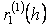жңне 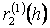жуықтау қателіктерін былайша баѓалауѓа болады:

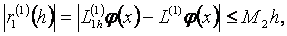(1.2.3)

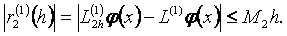(1.2.4)

Дңл осы жолмен Тэйлор қатарын пайдаланып,

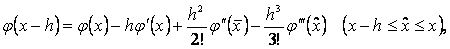
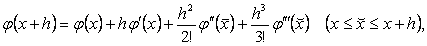
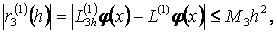(1.2.5)

баѓалауын аламыз. Мђндаѓы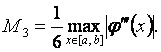

Жоѓарыда айтылѓан (1.2.3), (1.2.4) жңне (1.2.5) баѓалауларын сипаттау џшін келесі анықтаманы енгіземіз.

Анықтама.Егер белгілі бір Ф функциялар жиыныныњ 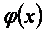элементтері џшін

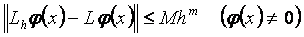
Шарты орындалса, онда 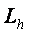айырымдық операторы 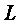операторына Ф де 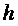бойынша реті 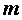-ге тењ дңлдікпен жуықтайды деп атайды. Мђндаѓы 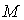шамасы 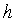-қа тңуелсіз тђрақты сан.

Осы анықтамаѓа сџйеніп (1.2.3), (1.2.4) жңне (1.2.5) баѓалауларынан мынадай мањызды қорытындылар шыѓарамыз: егер 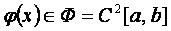болса, онда 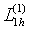жңне 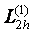айырымдық операторлары 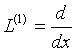операторына бірінші ретпен жуықтайды (m=1). Ал 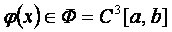болѓан жаѓдайда 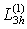операторыныњ жуықтау реті екіге тењ (m=2) болады.

2⁰.Енді 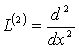екінші ретті жай дифференциалдық операторын жуықтату мңселесіне тоқталайық. Оны мына айырымдық оператор арқылы жуықтатуѓа болады:

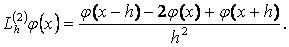
Бђл оператордыњ жуықтау ретін анықтау џшін тљмендегі Тэйлор қатарларын пайдаланамыз:

,

.

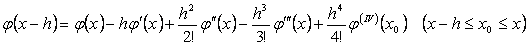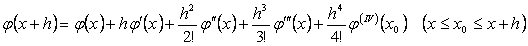Онда

.

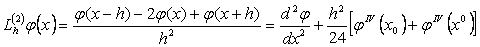Айталық, 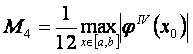болсын. Ендеше соњѓы тењдіктен келесі баѓалауды алу қиын емес

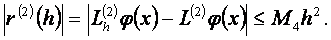
Демек, анықтамаѓа сңйкес, 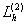айырымдық операторы 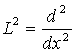операторын 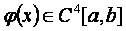функциялар жиынында екінші ретпен жуықтайды (m=2).

3⁰.Мына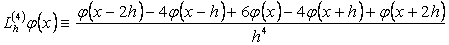

айырымдық оператордыњ 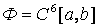жиынында 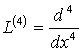операторына екінші ретпен жуықтайды.