Возрастание и убывание функций. Экстремумы функции
Функция 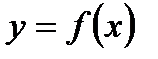 называется возрастающей в некотором промежутке
называется возрастающей в некотором промежутке 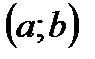 , если для любых двух значений
, если для любых двух значений 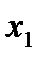 и
и 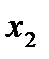 , принадлежащих этому промежутку, из неравенства
, принадлежащих этому промежутку, из неравенства
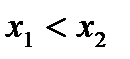 следует неравенство
следует неравенство 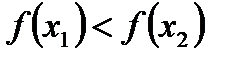 (рис.1)
(рис.1)
Функция 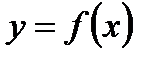 называется убывающей в некотором промежутке, если для любых двух значений
называется убывающей в некотором промежутке, если для любых двух значений 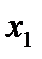 и
и 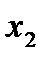 , принадлежащих этому промежутку, из неравенства
, принадлежащих этому промежутку, из неравенства
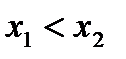 следует неравенство
следует неравенство 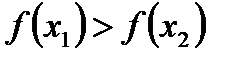 (рис.2)
(рис.2)


рис.1 рис.2
Теорема. Если в данном промежутке 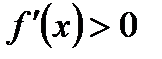 , то функция возрастает в этом промежутке; если же
, то функция возрастает в этом промежутке; если же 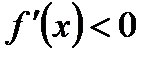 , то функция убывает в соответствующем промежутке.
, то функция убывает в соответствующем промежутке.
Теорема имеет простой геометрический смысл. Если в некотором промежутке касательная к графику функции 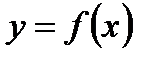 образует с осью
образует с осью 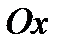 острый угол
острый угол 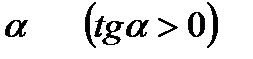 , то функция возрастает в этом промежутке. Если касательная к графику образует с осью
, то функция возрастает в этом промежутке. Если касательная к графику образует с осью 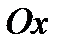 тупой угол
тупой угол 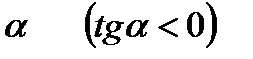 , функция убывает.
, функция убывает.
Интервалы, на которых функция только возрастает или же только убывает, называются интервалами монотонности функции, а сама функция называется монотонной на этих интервалах.
Геометрически ясно, что функция будет монотонной и в том случае, когда её производная, сохраняя всё время постоянный знак, обращается в отдельных точках в нуль, касательная в которых параллельна оси 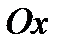 .
.
Например, функция 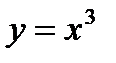 возрастает в любом интервале, так как её производная
возрастает в любом интервале, так как её производная 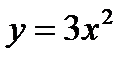 всё время положительна, кроме точки
всё время положительна, кроме точки 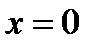 , где она обращается в нуль.
, где она обращается в нуль.
Экстремумы функций.
Точка 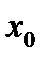 из области определения функции
из области определения функции 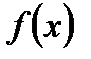 называется точкой максимума (минимума) этой функции, если существует такая δ - окрестность точки
называется точкой максимума (минимума) этой функции, если существует такая δ - окрестность точки 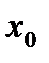 , что для всех
, что для всех 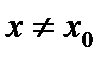 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 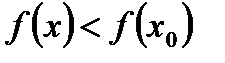
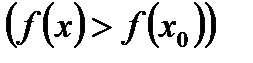 .
.
Другими словами, максимумом (минимумом) функции 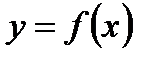 называют такое её значение, которое больше (меньше) всех других значений, принимаемых в точках, достаточно близких к данной и отличных от неё.
называют такое её значение, которое больше (меньше) всех других значений, принимаемых в точках, достаточно близких к данной и отличных от неё.
Если в точке 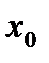 функция имеет максимум или минимум, то говорят, что в точке
функция имеет максимум или минимум, то говорят, что в точке 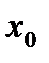 имеет место экстремум, значение функции в этой точке называется экстремальным, точка
имеет место экстремум, значение функции в этой точке называется экстремальным, точка 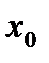 называется точкой экстремума.
называется точкой экстремума.
Необходимое условие экстремума.
Если точка 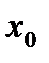 является точкой экстремума функции, то
является точкой экстремума функции, то 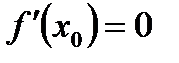 или
или 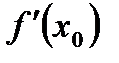 не существует.
не существует.
Точки, в которых производная равна нулю или не существует, называются критическими точками.
Однако не всякая критическая точка является точкой экстремума, поэтому необходимо в каждой критической точке проверить, выполняется ли достаточное условие экстремума.
Первое достаточное условие экстремума функции.
Пусть функция 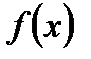 дифференцируема в некоторой δ - окрестности критической точки
дифференцируема в некоторой δ - окрестности критической точки 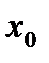 . Тогда, если
. Тогда, если 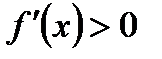
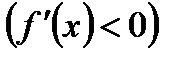 для всех
для всех 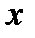 из
из 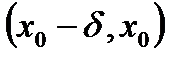 , а
, а 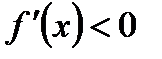
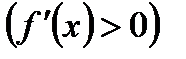 для всех
для всех 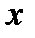 из
из 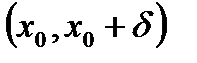 , то в точке
, то в точке 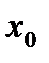 функция
функция 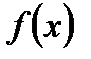 имеет максимум (минимум); если же
имеет максимум (минимум); если же 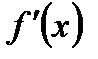 во всей δ-окрестности точки
во всей δ-окрестности точки 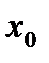 имеет один и тот же знак, то в точке
имеет один и тот же знак, то в точке 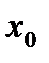 экстремума нет.
экстремума нет.
Другими словами, если 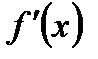 при переходе через критическую точку
при переходе через критическую точку 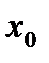 меняет знак с «+» на «-», то
меняет знак с «+» на «-», то 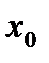 - точка максимума; если
- точка максимума; если 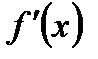 при переходе через точку
при переходе через точку 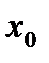 меняет знак с «-» на «+», то в этой точке функция достигает минимума. Если же при переходе через критическую точку первая производная знака не меняет, то экстремума нет.
меняет знак с «-» на «+», то в этой точке функция достигает минимума. Если же при переходе через критическую точку первая производная знака не меняет, то экстремума нет.
Второе достаточное условие экстремума функции.
Критическая точка 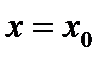 является точкой экстремума функции, если первая не обращающаяся в нуль производная в этой точке имеет четный порядок. При этом, если эта производная отрицательна (положительна), то критическая точка
является точкой экстремума функции, если первая не обращающаяся в нуль производная в этой точке имеет четный порядок. При этом, если эта производная отрицательна (положительна), то критическая точка 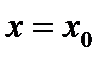 является точкой максимума (минимума).
является точкой максимума (минимума).
Например, пусть выполнены условия 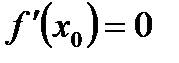 и
и 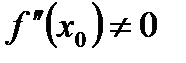 , тогда:
, тогда:
если 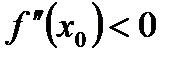 , то
, то 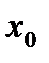 - точка максимума функции
- точка максимума функции 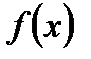 ;
;
если 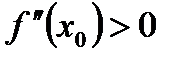 , то
, то 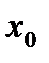 - точка минимума функции
- точка минимума функции 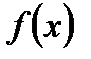 .
.
Пример 1. Исследовать на экстремум функцию
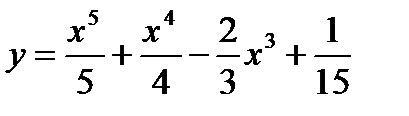 .
.
Решение. Областью определения данной функции является вся числовая прямая.
Находим производную данной функции: 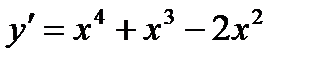 . Используя необходимое условие экстремума, получаем уравнение для нахождения критических точек:
. Используя необходимое условие экстремума, получаем уравнение для нахождения критических точек: 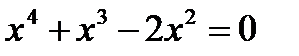 .
.
Решаем это уравнение:
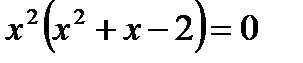 , (*)
, (*)
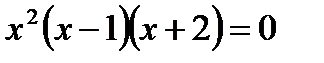 ;
;
Находим критические точки: 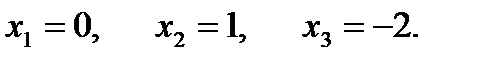
Рассмотрим интервалы: 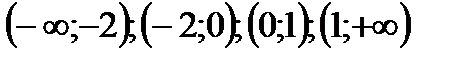 .
.
Выбираем внутри каждого из этих интервалов произвольную точку и определяем знак первой производной, используя уравнение (*). Результаты удобно оформить в виде рисунка.

Итак, в точке 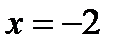 первая производная меняет знак с «+» на «-», следовательно, в точке
первая производная меняет знак с «+» на «-», следовательно, в точке 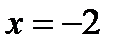 функция имеет максимум,
функция имеет максимум, 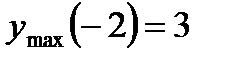 ; в точке
; в точке 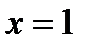 первая производная меняет знак с «-» на «+», следовательно, в точке
первая производная меняет знак с «-» на «+», следовательно, в точке 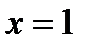 данная функция достигает минимального значения,
данная функция достигает минимального значения, 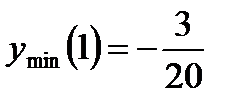 . В точке
. В точке 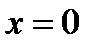 экстремума нет, так как производная знака не меняет.
экстремума нет, так как производная знака не меняет.
Пример2. Исследовать на экстремум функцию
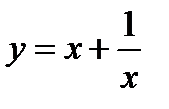 .
.
Решение. Область определения данной функции: 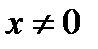 , т.е.
, т.е. 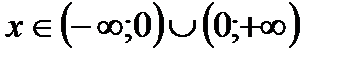 .
.
Находим первую производную: 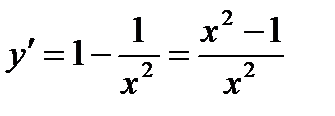 .
.
Тогда при 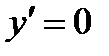 критические точки
критические точки 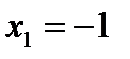 ,
, 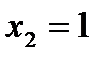 ,
, 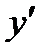 не существует при
не существует при 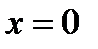 , но эта точка не принадлежит области определения функции, следовательно, не может быть точкой экстремума.
, но эта точка не принадлежит области определения функции, следовательно, не может быть точкой экстремума.
Для выяснения характера критических точек воспользуемся вторым достаточным условием экстремума.
Находим вторую производную: 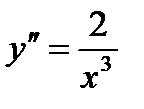 .
.
Определяем знак второй производной в критических точках: 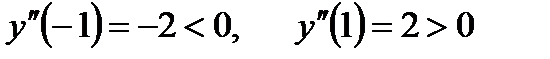 , т.е. в точке
, т.е. в точке 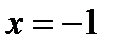 данная функция имеет максимум,
данная функция имеет максимум, 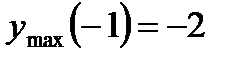 ; в точке
; в точке 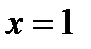 - минимум,
- минимум, 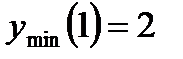 .
.
