Интерполяционный полином Лагранжа
ОТЧЕТ
по лабораторной работе №1
Вариант № 23
по курсу «Информатика»
Проверил:
___________ Ю.А. Кудинов
« » декабря 2013 г.
Выполнил:
студент группы З-12Стр(б)ПГС
__________ А.С. Усимбеков
« » декабря 2013 г.
Оренбург 2013
Содержание
1 Постановка задачи. 3
2 Метод половинного деления. 4
3 Метод хорд. 6
4 Метод Ньютона. 7
5 Метод простых итерации. 8
6 Интерполяционный полином Лагранжа. 9
Постановка задачи
Цель работы: научиться работать в среде Excel, изучите методы вычислительной математики.
Задания
Решить уравнение f(x)=0.
1 этап – построить график функции y=f(x) на интервале p1 < x < p2, отрезок [p1,p2] должен быть больше отрезка [a,b] указанного в таблице (или p1 < min «a», p2 > max «b» если в таблице указано несколько отрезков). Определить отрезки с изолированными корнями.
2 этап - уточнить корни уравнения с точностью до e = 0,001 методом половинного деления, методом хорд, методом Ньютона.
Таблица 1 - Вариант задания
| N варианта | f(x)=0 | [a,b] |
| 23. | x tg x - 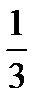 = 0 = 0 | [-2.4;0.57] |
3 Найти решение системы линейных уравнений методом простой итерации с точностью e=10-3.
10x1+x2-x3 = 0
-x1-13x2+x3 = 1
4x1+x2+7x3 = 4
4 Задания. Дана таблично заданная функция f(x). Используя интерполяционный полином Лагранжа L(x), вычислить приближенное значение функции f(x) в произвольно выбранной точке «x», принадлежащей заданному интервалу xk.
Таблица 2 – Вариант задания
| № варианта | Значения функции f(x) в узлах интерполяции xk | ||||
| xk | 1.00 | 1.06 | 1.12 | 1.19 | |
| f(x) | 1.17 | 1.27 | 1.36 | 1.49 |
Метод половинного деления
Задание
Решить уравнение f(x)=0.
1 этап – построить график функции y=f(x) на интервале p1 < x < p2, отрезок [p1,p2] должен быть больше отрезка [a,b] указанного в таблице (или p1 < min «a», p2 > max «b» если в таблице указано несколько отрезков). Определить отрезки с изолированными корнями.
2 этап - уточнить корни уравнения с точностью до e = 0,001 методом половинного деления.
Таблица 3 - Вариант задания
| N варианта | f(x)=0 | [a,b] |
| 23. | x tg x - 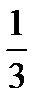 = 0 = 0 | [-2.4;0.57] |
На рисунке 1 представлен график заданной функции.
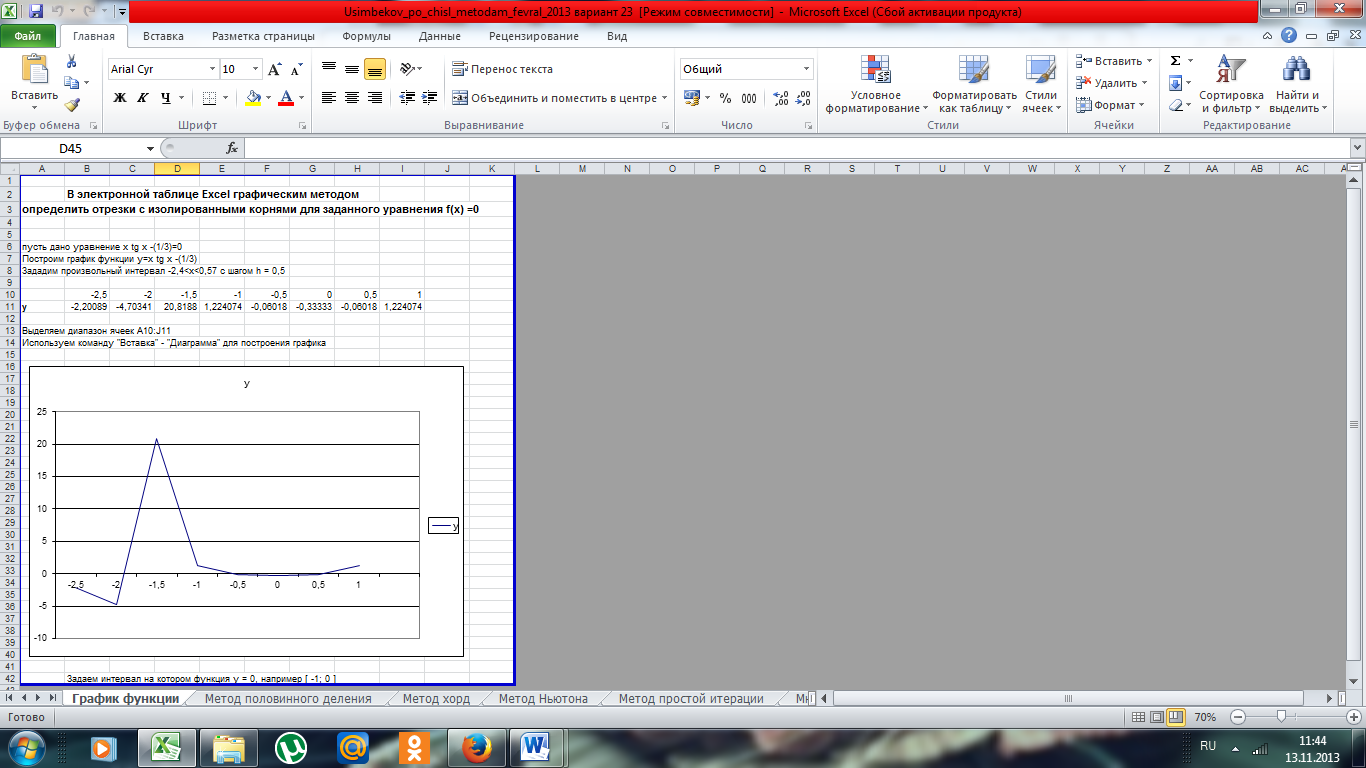
Рисунок 1- Скриншот построения графика функции
На рисунке 2 представлено решение нелинейного алгебраического уравнения методом половинного деления.
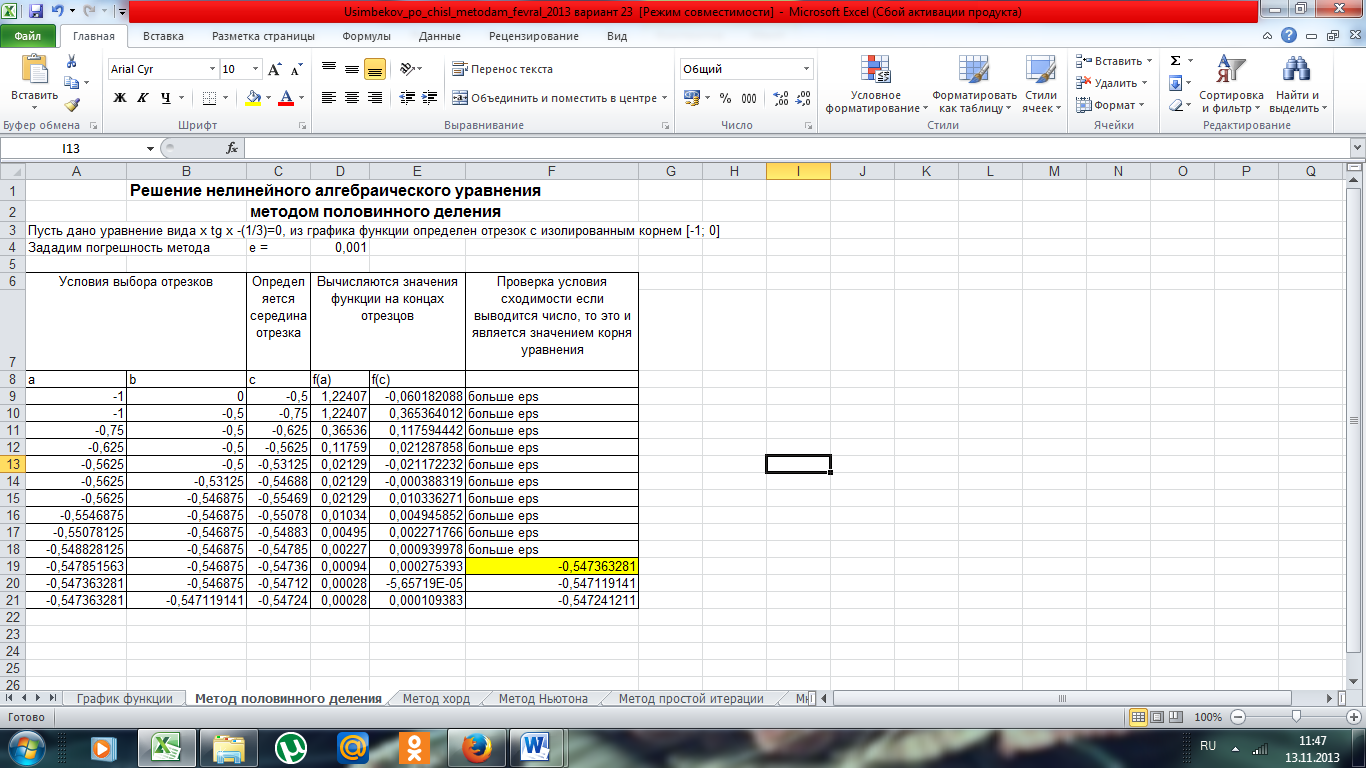
Рисунок 2 - Скриншот решения нелинейного алгебраического уравнения методом половинного деления
Метод хорд
Задание
Решить уравнение f(x)=0.
1 этап – построить график функции y=f(x) на интервале p1 < x < p2, отрезок [p1,p2] должен быть больше отрезка [a,b] указанного в таблице (или p1 < min «a», p2 > max «b» если в таблице указано несколько отрезков). Определить отрезки с изолированными корнями.
2 этап - уточнить корни уравнения с точностью до e = 0,001 методом хорд.
Таблица 4 - Вариант задания
| N варианта | f(x)=0 | [a,b] |
| 23. | x tg x - 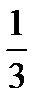 = 0 = 0 | [-2.4;0.57] |
На рисунке 3 представлен график заданной функции.
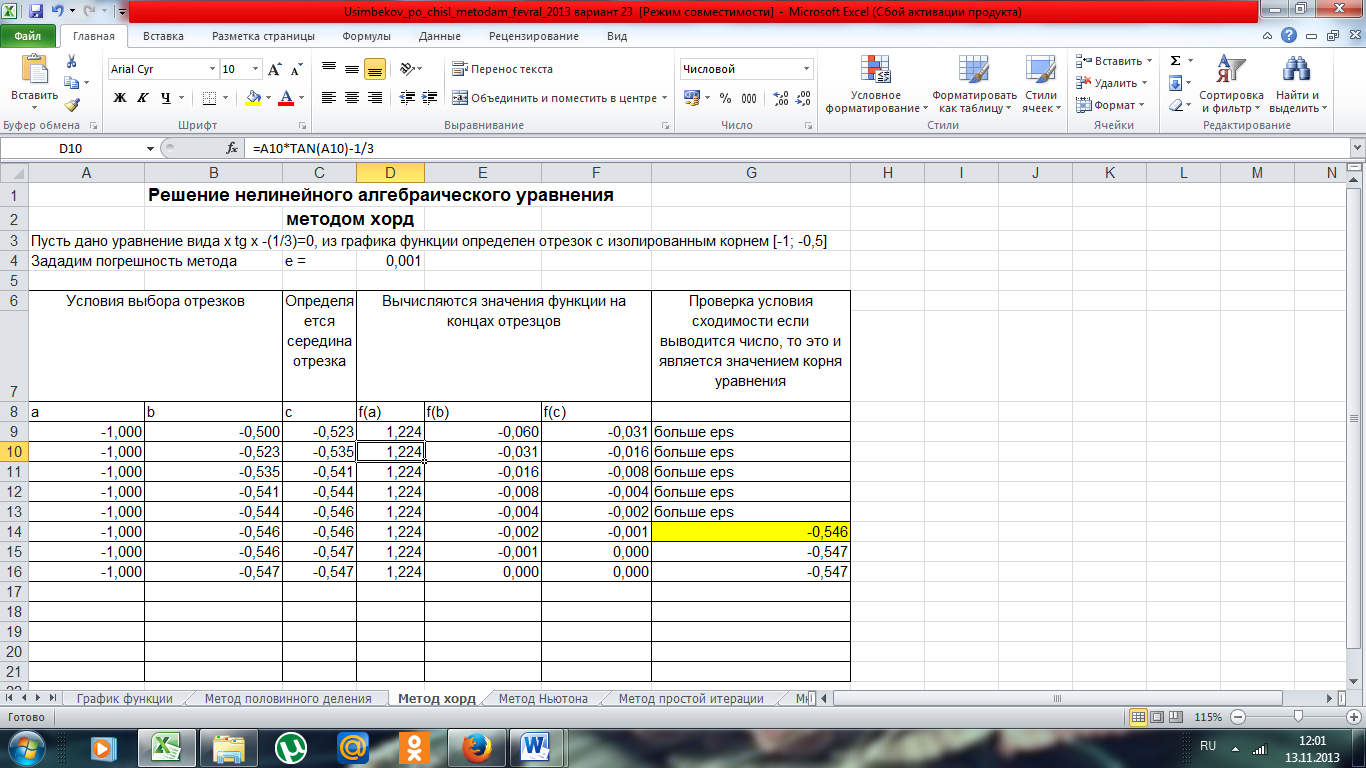
Рисунок 3 - Скриншот решения нелинейного алгебраического уравнения методом хорд
Метод Ньютона
Задание
Решить уравнение f(x)=0.
1 этап – построить график функции y=f(x) на интервале p1 < x < p2, отрезок [p1,p2] должен быть больше отрезка [a,b] указанного в таблице (или p1 < min «a», p2 > max «b» если в таблице указано несколько отрезков). Определить отрезки с изолированными корнями.
2 этап - уточнить корни уравнения с точностью до e = 0,001 методом Ньютона.
Таблица 5 - Вариант задания
| N варианта | f(x)=0 | [a,b] |
| 23. | x tg x - 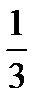 = 0 = 0 | [-2.4;0.57] |
На рисунке 4 представлен график заданной функции.
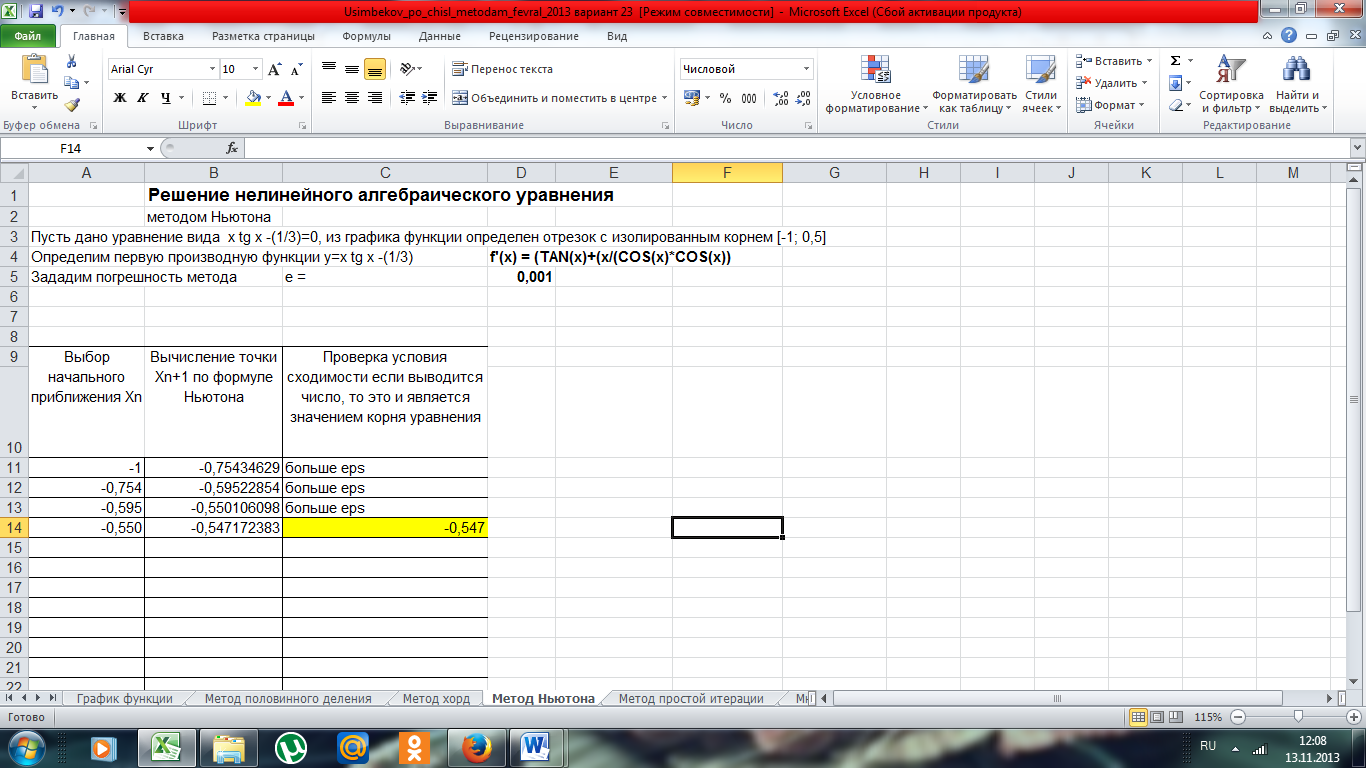
Рисунок 4 - Скриншот решения нелинейного алгебраического уравнения методом Ньютона
Метод простых итерации
Найти решение системы линейных уравнений методом простой итерации с точностью e=10-3.
10x1+x2-x3 = 0
-x1-13x2+x3 = 1
4x1+x2+7x3 = 4
На рисунке 5 представлено решение системы методом простых итераций.
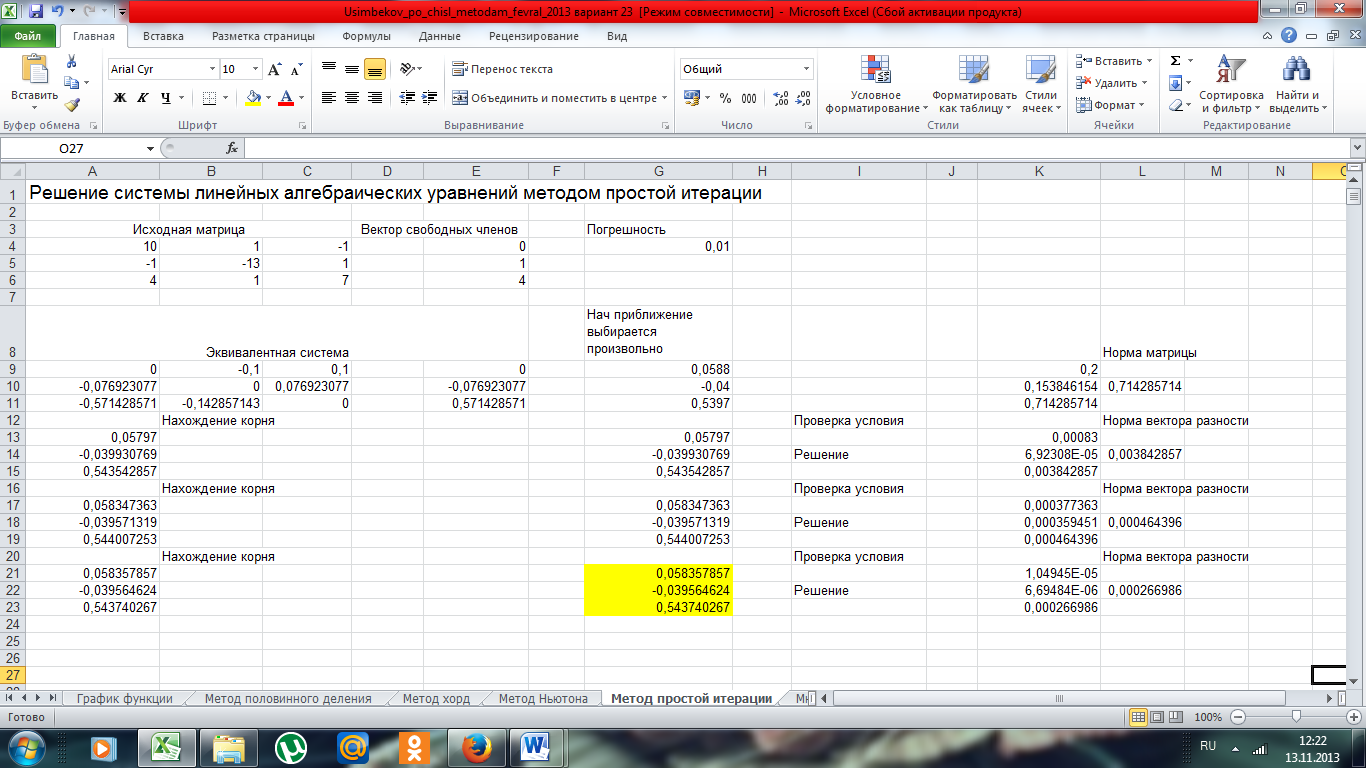
Рисунок 5 - Скриншот решения системы методом простых итерации
Интерполяционный полином Лагранжа
Задание
Дана таблично заданная функция f(x). Используя интерполяционный полином Лагранжа L(x), вычислить приближенное значение функции f(x) в произвольно выбранной точке «x», принадлежащей заданному интервалу xk.
Таблица 6 – Вариант задания
| № варианта | Значения функции f(x) в узлах интерполяции xk | ||||
| xk | 1.00 | 1.06 | 1.12 | 1.19 | |
| f(x) | 1.17 | 1.27 | 1.36 | 1.49 |
На рисунке 6 представлено решение системы методом простых итераций.
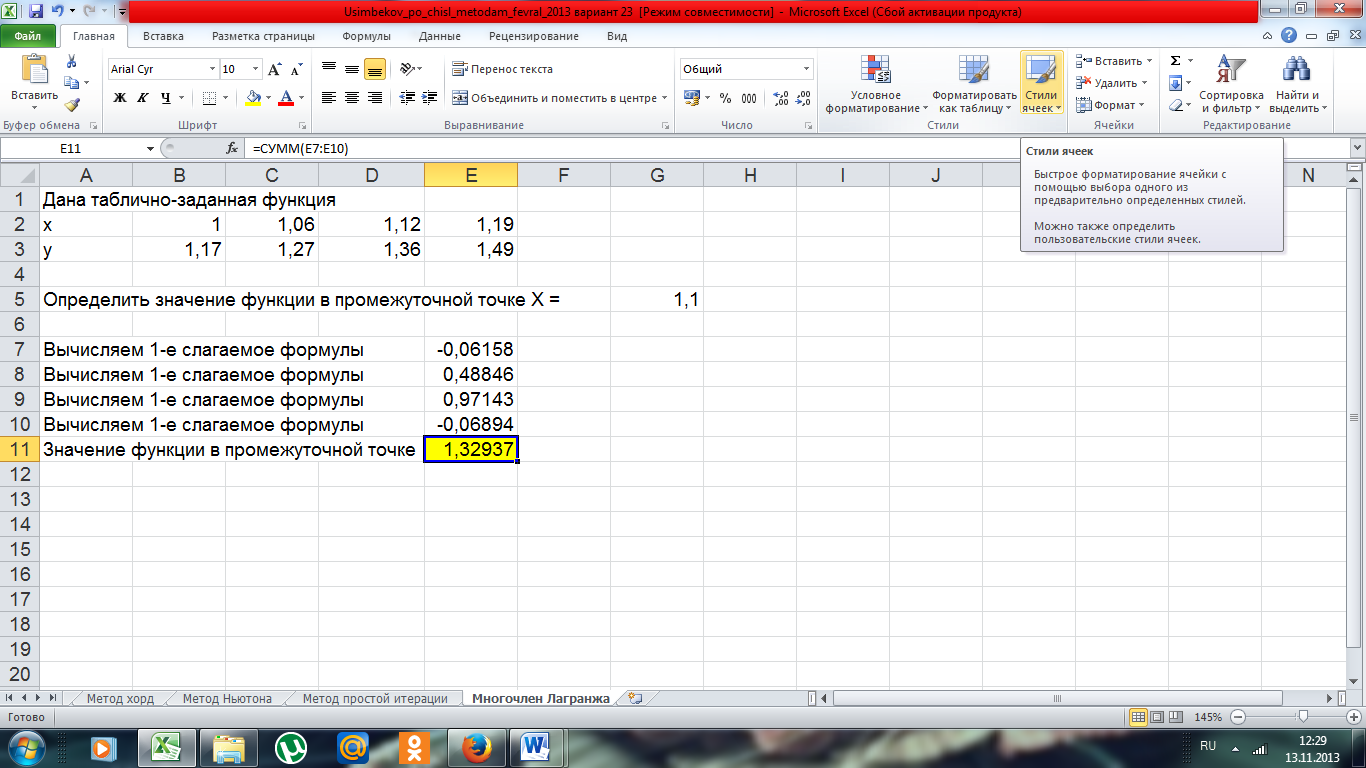
Рисунок 6 - Скриншот решения
