Часові характеристики. Частотні характеристики. Логарифмічні частотні характеристики. Співвідношення взаємозв'язку характеристик САК між собою та передатньою функцією.

Основні поняття ТАК

Предмет і завдання курсу. Сутність автоматичного керування. Предмет і завдання курсу. Місце ТАК в системі наук. Основні визначення. Завдання автоматичного керування. Принципи автоматичного керування. Види впливів на САК. Режими роботи САК. Вимоги до САК. Класифікація САК. Узагальнена функціональна схема САК.

ТАК є теоретичною основою технічної кібернетики - напрямку кібернетики, що займається вивченням технічних систем.

Сама ж кібернетика (з грецьк.– мистецтво керування) є наукою про керування, зв'язок і переробку інформації

Основними об'єктами дослідження в кібернетиці є кібернетичні системи(КС). Особливістю цих систем є те, що їх розглядають абстрактно, тобто безвідносно від їхньої реальної природи. Абстрактну КС представляють у вигляді сукупності взаємозалежних об'єктів - елементів системи, здатних запам'ятовувати та переробляти інформацію, а також обмінюватися нею з іншими елементами та зовнішнім світом.

Одним з найбільш прогресивних напрямків у загальному розвитку науки й техніки є заміна операцій людини в процесах керування функціонуванням певних технічних пристроїв, тобто автоматизація таких процесів.

При цьому все більшого значення набуває автоматичне керування, під яким мається на увазі здійснення певних керуючих впливів на заданий об'єкт, необхідних і достатніх для його цілеспрямованого функціонування із заданою точністю без особистої участі людини.

Найбільш загальними, що лежать в основі всієї термінології ТАУ визначеннями є наступні поняття: алгоритм, алгоритм функціонування, об'єкт керування, алгоритм керування, керування, автоматичний керуючий пристрій, система автоматичного керування.

Алгоритмом називають сукупність приписань, що встановлюють кінцеву послідовність певних дій, виконання яких приводить до кінцевого результату.

Алгоритм функціонування – це сукупність приписань, що ведуть до правильного виконання технічного процесу у пристрої або в сукупності пристроїв (системі). Наприклад, алгоритм функціонування генератора змінного струму, призначеного для перетворення теплової енергії в електричну, часто формулюється у вигляді - забезпечення сталості параметрів напруги 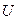та частоти 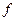, тобто 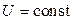і .

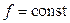У ТАК алгоритм функціонування вважається заданим.

Об'єкт керування (ОК) – це пристрій (або сукупність пристроїв), що здійснює технічний процес і потребує спеціально організованих впливів ззовні для забезпечення свого алгоритму функціонування.

Алгоритм керування – це сукупність приписань, що визначають характер впливів на ОК з метою забезпечення його алгоритму функціонування.

Керування - процес виконання впливів на ОК відповідно до алгоритму керування.

Автоматичний керуючий пристрій (АКП) – це пристрій, що здійснює без участі людини процес керування.

Система автоматичного керування (САК) – сукупність ОК і АКП, взаємодіючих між собою з метою забезпечення заданого алгоритму функціонування ОК.

САК можна представити у вигляді функціональної схеми, наведеної на рис. 1.1.

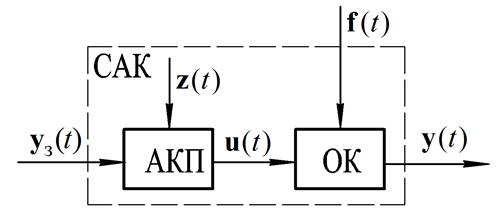
Рис. 1.1

Залежно від характеру завдань керування можна виділити наступні узагальнені види цілей функціонування САК: стабілізація, програмне керування та спостереження.

Під принципами керування в ТАК розуміють способи формування керуючого впливу.

Незважаючи на величезне різноманіття реальних САК, усі вони будуються з використанням двох основних принципів керування.

Принцип керування по відхиленню, основною ознакою якого є наявність зворотнього зв'язку (замкненого контуру проходження сигналу), коли керуючий вплив визначається з урахуванням фактичного стану виходу ОК (рис. 1.2).

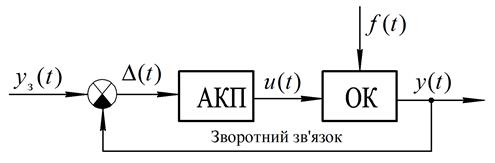
Рис. 1.2

У цих САК керуючий вплив визначається не безпосередньо по керованій величині 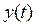, а за величиною сигналу помилки 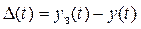, тобто 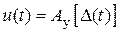, де 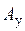- оператор перетворення (алгоритм керування).

Принцип розімкненого керування, коли відсутній облік значень керованої величини. Реалізується він розімкненими САК, які, у свою чергу, діляться на два класи:

- САК, що здійснюють керування за збурюючим впливом;

- САК, що здійснюють керування за задаючим впливом.

У першому випадку функціональна схема САК має вигляд, наведений на рис.1.3.

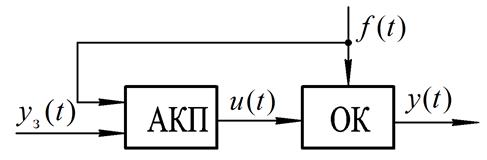
Рис. 1.3

У таких системах визначення керуючого впливу 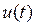здійснюється з урахуванням інформації про величину збурюючого впливу 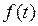, тобто

.

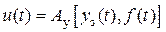У другому випадку САК має вигляд, наведений на рис.1.4.

Рис. 1.4

Сутність такого керування полягає в тому, що керуючий вплив формується тільки на основі задаючого впливу, тобто

.

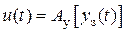САК в ході свого функціонування випробовують впливи двох видів: внутрішні і зовнішні.

Внутрішні впливи виникають у результаті взаємодії елементів САК між собою. Типовим прикладом такого впливу є дія АКП на ОК.

Зовнішні впливи виникають поза САК і можуть передаватися в систему як через ОК, так і через будь-який інший елемент системи. Цими впливами є задаючий і збурюючий впливи.

Дослідження функціонування конкретних САК роблять при декількох різних, чітко визначених впливах, називаних типовими.

До цих впливів відносяться.

Східчастий вплив – вплив, що миттєво зростає від нуля до деякого значення і далі залишається постійним (див. рис. 1.5а).

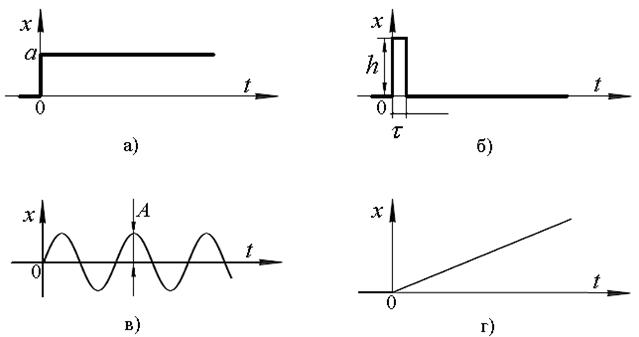
Рис. 1.5 - Види типових впливів САК

Імпульсний вплив – вплив, що представляє собою одиночний імпульс прямокутної форми, який має досить велику висоту 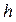(див. рис. 1.5б) і істотно меншу в порівнянні з інерційністю системи тривалість .

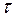Найбільш часто використовують одиничний імпульсний вплив 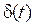, що описується так називаною дельта-функцією:

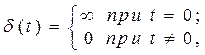причому .

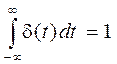Гармонійний вплив – вплив, описуваний функцією

,

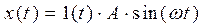де: 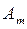- амплітуда, а - 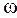частота зміни (див. Рис. 1.5в).

Лінійний вплив – вплив, описуваний функцією 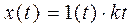(див. рис. 1.5г).

Будь-яка САК в процесі роботи може перебувати у двох якісно відмінних один від одного режимах залежно від характеру зовнішніх впливів і властивостей самої системи. Розрізняються ці режими по характеру зміни керованої величини в часі і називаються статичним і динамічним.

Статичним режимом називають стан системи, при якому керована величина 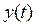не змінюється в часі, тобто .

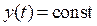Цей режим може мати місце лише тоді, коли вхідні впливи постійні в часі, а система перебуває в рівноважному стані.

Динамічним режимом називають стан системи, при якому величина 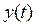змінюється в часі, тобто .

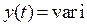Ефективність САК в кожному конкретному випадку залежить від того, наскільки система задовольняє пропонованим до неї вимогам. Основною вимогою є забезпечення заданої функціональної залежності між задаючим впливом на вході і керованою змінною на виході системи. Ідеальних систем, які виконували б ці вимоги абсолютно точно, не існує. Тому мова може йти лише про ступінь наближення роботи реальної системи до ідеалу. Для оцінки цього наближення використовують наступні категорії вимог:

- по запасу стійкості системи;

- по величині помилки в сталому стані або статичній точності;

- по поводженню системи в перехідному процесі (сукупність цих вимог називається умовами якості);

- по динамічній точності системи, тобто по величині помилки при безупинно змінюючихся впливах.

При вивченні конкретної САК її зручно попередньо формально розділити на окремі типові елементи, виявити взаємозв'язки між цими елементами і відобразити їх у вигляді функціональної схеми. Функціональною схемою САК називають умовне графічне зображення, що відбиває функції, які виконують окремі елементи системи та зв'язки між цими елементами.

Елементи САК можуть бути зведені до декількох основних типів, що розрізняються по їхньому призначенню. Відповідно до цього можна говорити про узагальнену функціональну схему. Така схема представлена на рис. 1.6.

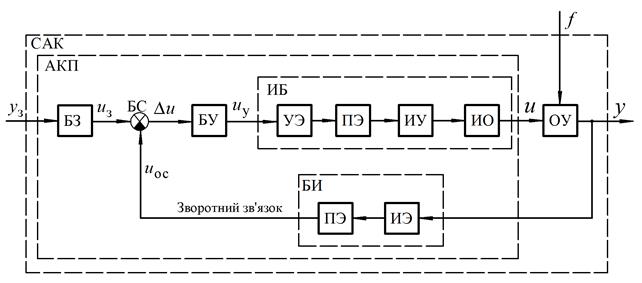
Рис. 1.6 – Узагальнена функціональна схема САК

Частинами функціональної схеми є умовні зображення функціональних блоків і елементів, а також зв'язків між ними у вигляді ліній зі стрілками. Стрілки показують напрямок передачі сигналів взаємодії. Функціональні блоки та елементи зображають у вигляді прямокутників, усередині яких записують їхню назву.

Приклад 1. Скласти функціональну схему системи стабілізації швидкості обертання електродвигуна постійного струму незалежного збудження, принципова схема якої наведена на рис. 1.7.

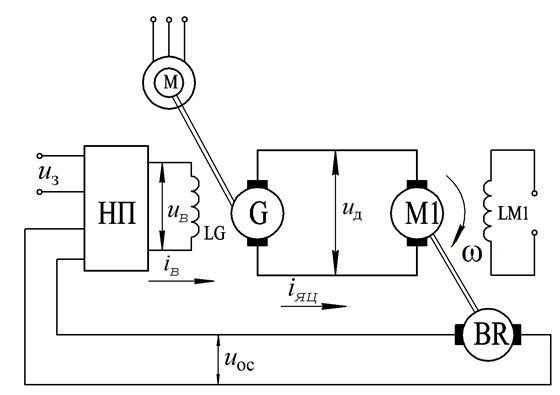
Рис. 1.7

На схемі прийняті наступні позначення: 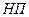– напівпровідниковий підсилювач; 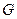– генератор постійного струму; 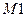- керований електродвигун постійного струму; 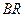– тахогенератор; 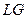, 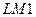– обмотки збудження, відповідно 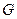і 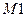; 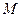– асинхронний привідний двигун з короткозамкненим ротором; 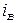– струм збудження; 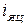– струм якірного ланцюга системи генератор-двигун; 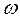– кругова частота обертання валу двигуна; 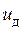– напруга на вихідних клемах генератора; 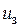- напруга сигналу завдання; 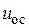- вихідна напруга тахогенератора.

Функціональну схему системи можна подати у вигляді, наведеному на рис.1.8.

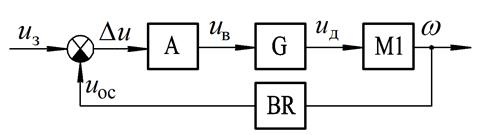
Рис. 1.8

Контрольні запитання

1. Назвіть завдання, які вирішуються в курсі теорії автоматичного керування.

2. Яку роль відіграє автоматизація на сучасному етапі розвитку науки і техніки?

3.Укажіть переваги та недоліки принципів керування, застосовуваних у САК.

4. Що таке функціональна схема САК?

5. На які класи діляться САК за метою керування?

6. На які класи ділять САК за виглядом математичного опису?

7. Що таке перехідний процес?

8. Які типові впливи використовуються при вивченні динаміки елементів і систем?

9. Які ознаки елементів системи керування відбиваються на її функціональній схемі?

10. Назвіть найпоширеніші функціональні елементи систем керування.

11. На які класи розділяють системи керування по величині помилки 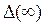в сталому режимі?

12. На які класи розділяються системи керування за принципом дії?

13. Які переваги та недоліки мають розімкнені системи керування?

14. Які переваги та недоліки мають замкнені системи керування?

Математичний опис САК

Математичний опис САК у змінних вхід - вихід. Стандартна форма запису диференціальних рівнянь САК. Операційний метод опису лінійних САК. Основні властивості перетворення Лапласа. Передатна функція. Властивості і особливості передатної функції. Лінеаризація рівнянь САК. Математичний опис САК у змінних стану. Стандартна форма запису рівнянь стану. Структурні схеми САК. Позначення в структурних схемах. Передатні функції типових з'єднань ланок. Додаткові правила перетворення структурних схем. Визначення передатних функцій замкнутої САК за структурною схемою.

Вирішення питань аналізу існуючих і синтезу нових САК можливе лише при наявності відповідного математичного опису їхніх властивостей. Цей опис називають математичною моделлю САК, тому що при її складанні завжди робляться ті або інші допущення і наближення.

При математичному описі САК застосовують два підходи: перший з них ґрунтується на поданні моделей у змінних вхід – вихід, а іншої – у змінних стану.

Математичний опис системи складається на основі опису всіх складових елементів.

Для САК, що має один вхід 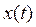і один вихід 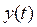, математичну модель можна представити у вигляді:

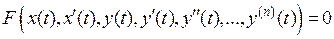. (2.1)

Для лінійної стаціонарної САК рівняння (2.1) є лінійним неоднорідним диференціальним рівнянням виду:

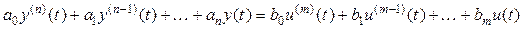, (2.2)

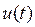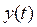де й – відповідно, вхідна і вихідна величини, що змінюються в часі; 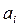, 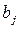– постійні коефіцієнти, обумовлені параметрами системи; 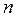– порядок рівняння.

При дослідженні САК, особливо при порівнянні властивостей систем і їхніх елементів між собою, зручно представляти рівняння в так званій стандартній формі. При цьому використовуються наступні правила:

– вихідну величину і всі її похідні записують у лівій частині рівняння, а всі інші члени – у правій;

– коефіцієнт при вихідній величині шляхом еквівалентних перетворень роблять рівним одиниці;

– якщо в правій частині є похідні, то члени, що містять певну вихідну величину і її похідні, поєднують в одну групу а коефіцієнт при цій величині виносять за дужки.

У ТАК саме широке застосування знайшов операційний метод опису, заснований на використанні інтегрального перетворення Лапласа (L- перетворення):

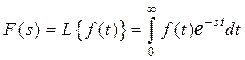. (2.3)

Це перетворення встановлює відповідність між функцією 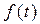дійсної змінної 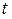і функцією 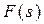комплексної змінної 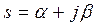. При цьому 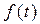називають оригіналом, а 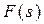- зображенням.

Перетворення Лапласа ставить у відповідність операціям над оригіналами деякі певні операції над зображеннями. У таблиці 2.1 наведені основні співвідношення, які використовуються при описі лінійних САК.

Застосування перетворення Лапласа при математичному описі САК обумовлюється також і тим, що з його допомогою визначають так називану передатну функцію, що є самою компактною формою опису властивостей САК або її складових елементів.

Передатною функцією називається відношення вихідної величини до вхідної, перетворених за Лапласом при нульових початкових умовах.

Таблиця 2.1 - Властивості перетворення Лапласа

Найменування властивості	Оригінал	Зображення
Лінійність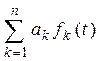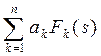
Диференціювання оригіналу при нульових початкових умовах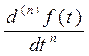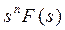
Інтегрування оригіналу при нульових початкових умовах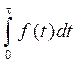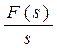
Зміна масштабу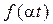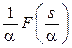
Зсув аргументу оригіналу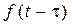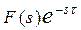
Згортка функцій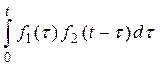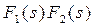
Початкове значення оригіналу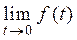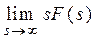
Кінцеве значення оригіналу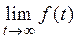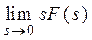

Рівняння багатьох реальних елементів і САК в цілому, тією чи іншою мірою є нелінійними. У цьому випадку змінні 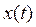, 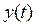і їхні похідні входять у вираз для функції 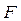у вигляді добутків, часток, степенів або інших більш складних функцій.

У зв'язку з складністю аналізу і рішення нелінійних рівнянь широко застосовується наближена їхня заміна на лінійні – лінеаризація.

У основу методу лінеаризації покладено розкладання в ряд Тейлора, що дозволяє розкласти нелінійну функцію декількох змінних за ступенями малих відхилень цих змінних на околицях значень, що відповідають заданому сталому режиму. За сталий режим може вибиратися режим, що існував до початку дії збурювання, або режим, що встановиться після загасання перехідного процесу.

Розглянемо нелінійне диференціальне рівняння другого порядку виду:

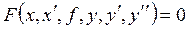. (2.4)

Перетворивши його, одержуємо остаточно:

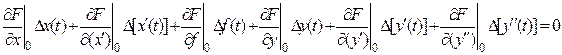. (2.5)

Як видно з (2.5), у результаті лінеаризації виходить рівняння у відхиленнях.

Метод змінних стану заснований на понятті стану.

Стан системи в момент часу 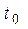- такий мінімальний набір відомостей про неї, якого разом із вхідною функцією 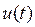, заданою для інтервалу часу 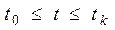, досить для однозначного визначення вихідної функції 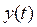, для 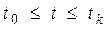при кожному .

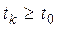Стан системи можна охарактеризувати сукупністю деяких змінних 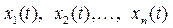, знання початкових значень яких 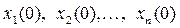і вхідного впливу 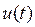дозволяє однозначно визначити майбутнє поводження динамічної системи. Ці змінні називаються змінними стану.

Щоб зв'язати послідовні стани системи в часі, використовують диференціальні рівняння:

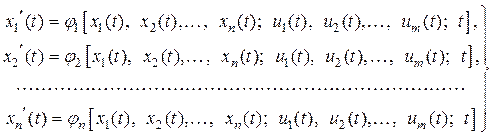. (2.6)

Праві частини цих рівнянь залежать від шуканих функцій 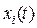і не залежать від їхніх похідних. Система рівнянь першого порядку виду (2.6)називається системою 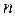диференціальних рівнянь, записаних в нормальній формі Коші.

В ТАК при аналізі САК саме широке застосування одержали так називані структурні схеми. При цьому під структурною схемою САК розуміють умовне графічне зображення математичної моделі системи у вигляді сукупності окремих ланок із вказівкою зв'язків між ними.

Правила зображення елементів САК на структурних схемах полягають у наступному.

1. Ланка позначається у вигляді прямокутника із вказівкою вхідних і вихідних величин.

а) б)

Рис. 2.1 - Зображення ланок

Усередині прямокутника вказується передатна функція (Рис.2.9,а).

Допускається замість вказувати рівняння або характеристику ланки (рис. 2.9,б). Позначення вхідних і вихідних величин записують у вигляді зображень або оригіналів залежно від позначення у прямокутнику. Допускається також ланки нумерувати, а їхні передатні функції, рівняння або характеристики представляти поза схемою.

2. Ланцюг передачі сигналу зображується прямою лінією на якій стрілкою вказується напрямок проходження сигналу, а також приводиться літерне позначення цього сигналу.

3. Елемент порівняння зображується у вигляді, наведеному на рис. 2.2.

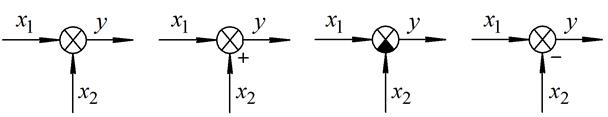
а) б)

Рис. 2.2 - Зображення елементів порівняння при реалізації функцій:

а) 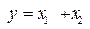; б)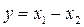

Структурна схема реальної САК звичайно може бути представлена у вигляді комбінації трьох типів з'єднань ланок: послідовного, паралельного та зустрічно-паралельного. Кожне із цих з'єднань може бути замінене за певними правилами однією ланкою, властивості якої будуть еквівалентними властивостям з'єднання.

Послідовне з'єднання.При такому з'єднанні вихідна величина поперед- ньої ланки є вхідною величиною наступної ланки (див. рис.2.3,а).

а) б)

Рис. 2.3 - Структурна схема послідовного з'єднання ланок:

а) вихідна; б) еквівалентна

Визначення еквівалентної передатної функції з'єднання 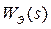по каналу 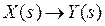- (див. Рис. 2.3,б) здійснюється за формулою:

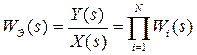. (2.7)

Паралельне з'єднання.При такому з'єднанні на вхід всіх ланок подається одна і та сама величина, а вихідна величина дорівнює сумі вихідних величин окремих ланок (див. рис. 2.4,а).

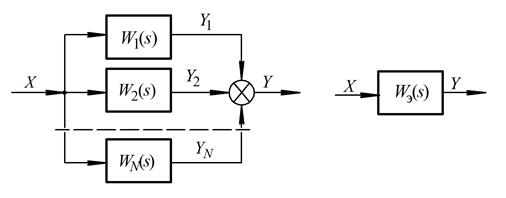
а) б)

Рис. 2.4 - Структурна схема паралельного з'єднання ланок:

а) вихідна; б) еквівалентна

Звідки:

. (2.8)

Зустрічно-паралельне з'єднання (охоплення ланки зворотнім зв'язком).У цьому випадку структурна схема має вигляд, наведений на Рис. 2.5,а, де зворотний зв'язок може бути як негативним, так і позитивним.

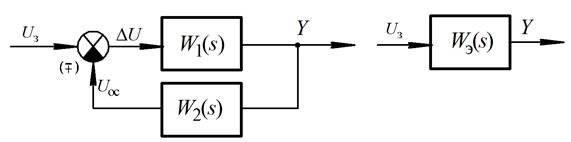
а) б)

Рис. 2.5 - Структурна схема зустрічно-паралельного з'єднання ланок:

а) вихідна; б) еквівалентна

Звідси остаточно маємо:

. (2.9)

Знак “+” в останній формулі ставиться у випадку негативного зворотнього зв'язку, а “-” - позитивного.

У ряді випадків вихідна структура САК може бути такою, що застосування описаних вище основних правил структурних перетворень виявляється недостатньою для її спрощення.

Найпоширеніші із цих правил наведені в табл.. 2.2, де всі змінні позначають сигнали, що з'явилися або зникли в результаті перетворень.

Таблиця 2.2 - Правила перетворення структурних схем САК

Операція	Вихідна схема	Перетворена схема
1. Перестановка суматорів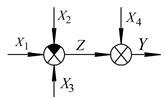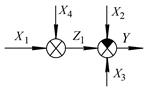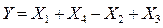
2. Перестановка вузлів розгалуження сигналів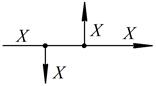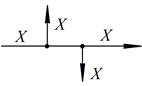
3. Перенесення суматора через ланку вперед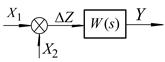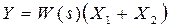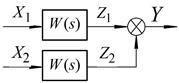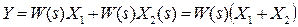
4. Перенесення суматора через ланку назад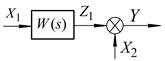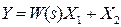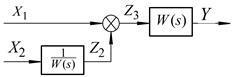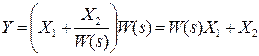
5. Перенесення вузла розгалуження через ланку вперед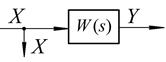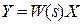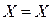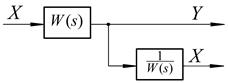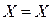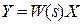
6. Перенесення вузла розгалуження через ланку назад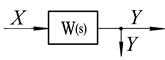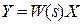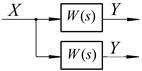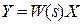

Користуючись отриманими правилами структурних перетворень, довільні структурні схеми реальних замкнутих САК можна перетворити до одноконтурного виду, наведеного на рис. 2.6.

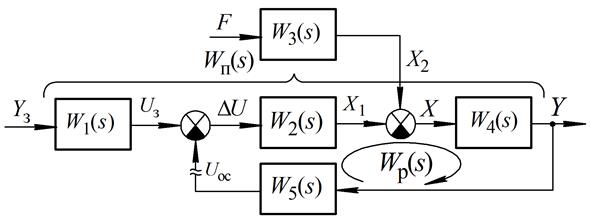
Рис. 2.6 - Узагальнена структура замкнутої САК

На основі схеми можна записати основні передатні функції САК, які встановлюють зв'язок керованої величини із вхідними впливами:

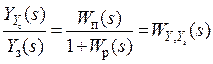. (2.10)

Величину 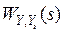називають передатною функцією замкнутої системи за задаючим впливом.

Аналогічним образом отримано величину

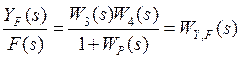(2.11)

називають передатною функцією замкнутої системи за збурюючим впливом.

До основних передатних функцій замкнутих САК відносять також функції, що встановлюють зв'язок сигналу неузгодженості 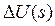із вхідними впливами. Застосувавши загальне правило, одержимо:

- для передатної функції за сигналом неузгодженості, викликаному задаючим впливом

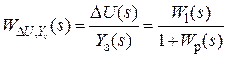; (2.12)

- для передатної функції за сигналом неузгодженості, викликаним збурюючим впливом

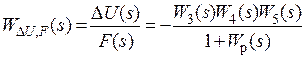, (2.13)

де 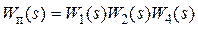- передатна функція прямого ланцюга (еквівалентна передатна функція між точкою додатка задаючого впливу і керованою величиною при розімкнутому контурі зворотного зв'язку) 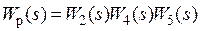; - передатна функція розімкнутого контуру, одержано при уявному розмиканні контуру (найчастіше, на ділянці дії сигналу зворотного зв'язку) щодо точок розмикання, обчислено без урахування передатної функції елемента порівняння.

Приклад 2.1.

Вихідне рівняння системи має вигляд:

.

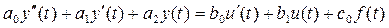Представимо це рівняння у стандартній формі.

Вирішення.

Маємо:

.

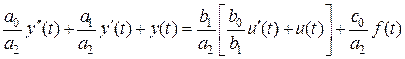Введемо позначення: ; ; ; ; .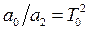

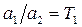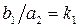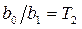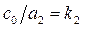Тоді:

.

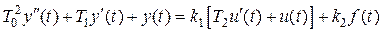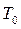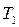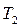Коефіцієнти , і мають розмірність часу, тому що

,

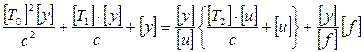і називаються постійними часу. Їхні значення визначають швидкість і характер протікання перехідних процесів.

Коефіцієнт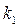и й 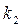називаються коефіцієнтами передачі, мають розмірність 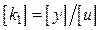, 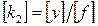і визначають взаємозв'язок змінних у сталих статичних режимах.

Приклад 2.2.

Нехай система описується рівнянням виду

.

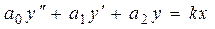Потрібно знайти передатну функцію 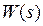системи при , , , .

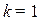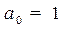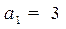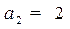Вирішення.

Перетворимо рівняння системи за Лапласом при нульових початкових умовах. Одержимо 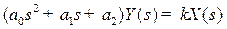. Звідки передатна функція буде:

.

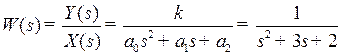Приклад 2.3.

Рівняння САК по каналу вхід-вихід має вигляд:

.

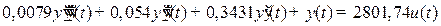Перетворити це рівняння в рівняння стану та вирішити їх.

Вирішення.

Перетворимо рівняння до нормованого вигляду:

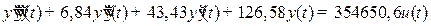. (2.14)

Позначимо: 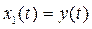; ; 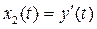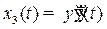і перетворимо вихідне рівняння до системи вигляду:

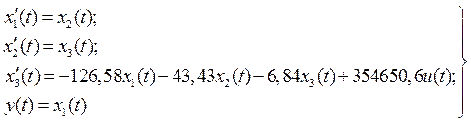. (2.15)

Тоді рівняння стану САК приймають вигляд:

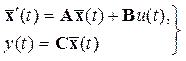, (2.16)

де

; ; ; .

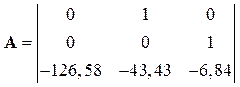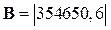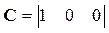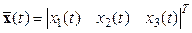Рішення системи (2.16) зручно робити за допомогою програми Simulink, скориставшись методом зниження порядку похідних.

Відповідна блок-схема наведена рис. 2.7.

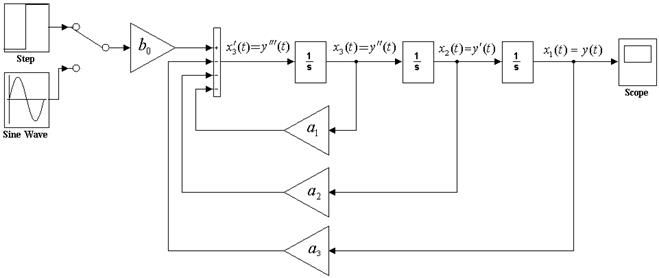
Рис. 2.7 - Блок-схема рішення диференціального рівняння третього порядку за допомогою програми Simulink

Контрольні запитання

1. Яке диференціальне рівняння називається лінійним?

2. Як складаються диференціальні рівняння елементів САК?

3. Поясніть суть лінеаризації.

4. Що називається передатною функцією САК або її елемента?

5. Як визначити вигляд передатної функції по заданому диференціальному рівнянню?

6. Наведіть перехідні характеристики типових ланок САК.

7. Що відбиває структурна схема системи керування?

8. Які вам відомі види з'єднання ланок та як визначити їхні передатні функції?

9. Назвіть види передатних функцій замкнутих САК.

10. Які системи називаються статичними і які астатичними?

11. Як визначити передатну функцію між довільними змінними струк- турної схеми САК?

12. Як з диференціального рівняння елемента одержати його рівняння статики?

13. Як одержати у загальному випадку з диференціального рівняння перехідну функцію?

14. Як зв'язані одна з одною перехідна та імпульсна функції?

15. Як з диференціального рівняння елемента одержати його передатну функцію?

16. Як від передатної функції елемента перейти до його рівняння динаміки у зображеннях, а потім у оригіналах?

17. За якими правилами визначаються еквівалентні передатні функції для послідовного, паралельного і зустрічно-паралельного з'єднань лінійних елементів? Запишіть відповідні формули для випадку двох з'єднаних елементів.

18. Що таке розімкнутий контур системи і чому дорівнює його передатна функція?

19. Як записується в загальному випадку характеристичне рівняння замк- нутої системи через передатну функцію розімкнутого контуру?

20. З яких складових складається сигнал помилки у типовій системі? Від яких зовнішніх впливів вони залежать?

21. Як зв'язані сигнал помилки і його складові з передатною функцією розімкнутого контуру?

Характеристики САК

Часові характеристики. Частотні характеристики. Логарифмічні частотні характеристики. Співвідношення взаємозв'язку характеристик САК між собою та передатньою функцією.

Диференціальні рівняння не залежно від форми подання є самою загальною формою опису САК і не дають наочного подання про всі її властивості. Більш наочно характеризують ці властивості функції 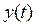, що є рішеннями диференціальних рівнянь. Найбільш широке використання при описі динамічних властивостей одержала перехідна функція 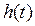. Перехідною функцією називають функцію, що описує зміну вихідної величини, яка виникає після подачі на вхід одиничного східчастого впливу 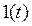при нульових початкових умовах. Графік перехідної функції називається перехідною характеристикою.

Другою часовою характеристикою є імпульсна перехідна функція 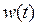. Під цією функцією мають на увазі функцію, що описує зміну вихідної величини, яка виникає після подачі на вхід дельта-функції при нульових початкових умовах. Графік 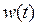називають імпульсною перехідною характеристикою.

Лінійні САК описуються диференціальними рівняннями вигляду:

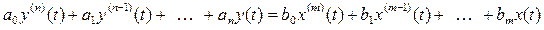, (3.1)

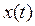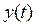де й – відповідно, вхідна і вихідна величини; 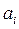, 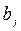– коефіцієнти; 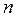– порядок рівняння.

З курсу вищої математики відомо, що інтегрування рівняння (3.1) зводиться до знаходження суми загального рішення однорідного рівняння без правої частини 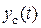і якого-небудь приватного рішення неоднорідного рівняння 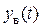, тобто:

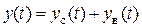. (3.2)

Зміна вихідної величини, обумовлена складовою 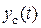називається вільним рухом, тому що залежить тільки від виду лівої частини рівняння (3.1), тобто від внутрішніх властивостей самого об'єкту. Складова 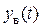, навпаки, залежить від характеру вхідного впливу і тому відповідна зміна називається змушеним рухом.

Складову 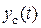шукаємо у вигляді

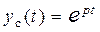, (3.3)

де 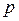– деяке раціональне число.

Підставивши (3.3) у рівняння (3.1) при нульовій правій частині, одержимо:

,

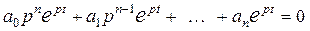або

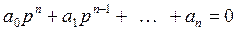. (3.4)

Останнє рівняння називається характеристичним.

Таким чином вираз (3.3) є рішенням вихідного рівняння за умови, що 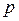є коренем рівняння (3.4). Оскільки це рівняння має 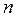коренів, то маємо і 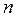лінійно незалежних рішень 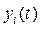. Скористаємося відомою теоремою математики, яка затверджує, що якщо 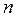лінійно незалежних функцій 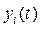є рішеннями однорідного рівняння, то загальне вирішення цього рівняння визначається виразом

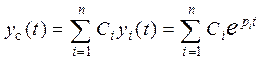, (3.5)

де 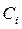– довільні постійні інтегрування.

Застосування перетворення Лапласа значно спрощує визначення часових характеристик.

Хід вирішення при цьому наступний.

1. Перетворимо вихідне рівняння (3.1) по Лапласу при нульових початкових умовах:

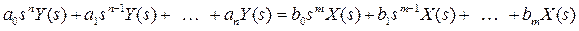. (3.6)

2. Вирішимо алгебраїчне рівняння (3.6) відносно 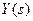при заданому :

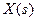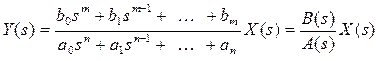. (3.7)

У випадку, якщо зображення є дрібно-раціональною функцією, тобто:

,

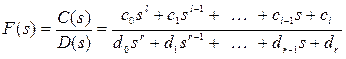причому 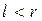, а коефіцієнти 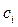, 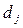- дійсні числа, застосовується формула розкладання Хевісайда:

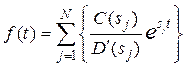. (3.8)

де 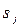- прості корені рівняння 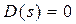; 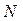- число коренів.

Частотні характеристики описують передатні властивості САК в режимі сталих гармонійних коливань, викликаних зовнішнім гармонійним впливом. Ці характеристики широко використовують в ТАК, тому що реальні зовнішні впливи можуть бути представлені у вигляді суми гармонійних сигналів. Вони визначаються змушеною складовою рішення диференціального рівняння при подачі на вхід впливу:

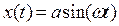. (3.9)

При гармонійному впливові на вході вихідна величина після закінчення перехідного процесу ( 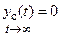) також змінюється за гармонійним законом, але з іншою амплітудою та фазою. При цьому відношення амплітуд вихідної і вхідної величин дорівнює модулю, а зрушення фаз – аргументу частотної передатної функції 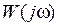- відношенню вихідної величини до вхідної, перетворених за Фур'є при нульових початкових умовах.

Крива, яку описує кінець вектора частотної передатної функції на комплексній площині при зміні частоти від 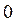до 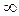називається амплітудно-фазовою частотною характеристикою (АФЧХ).

Крім АФЧХ, що є самою загальною частотною характеристикою, розрізняють наступні різновиди частотних характеристик:

-амплітудна частотна характеристика (АЧХ) – графік функції ;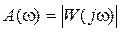

- фазова частотна характеристика (ФЧХ) – графік функції ;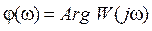

- речовинна частотна характеристика – графік функції ;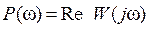

- уявна частотна характеристика – графік функції .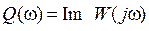

Дослідження частотних властивостей САК значно спрощується, якщо використати частотні характеристики, побудовані в логарифмічному масштабі. Такі характеристики називаються логарифмічними частотними характеристиками (ЛЧХ).

Для цього прологарифмуємо 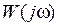, виражену в показовій формі:

.

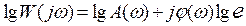Графік залежності 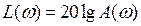, побудований у логарифмічному масштабі частот, називається логарифмічною амплітудною частотною характеристикою (ЛАЧХ).

Графік залежності фазової частотної функції 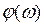від логарифму частоти називається логарифмічною фазовою частотною характеристикою ЛФЧХ.

Можливі співвідношення між характеристиками САК представлені в таблиці 3.1.

Таблиця 3.1 - Взаємозв'язок характеристик САК

Характеристика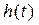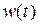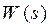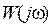
Перехідна характеристика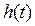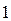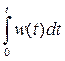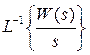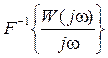
Імпульсна перехідна характеристика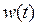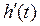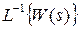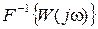
Передатна функція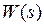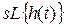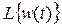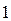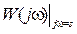
Частотна передатна функція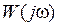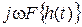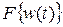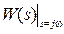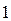

Приклад 3.1.

САК описується диференціальним рівнянням першого порядку:

,

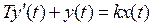де: , .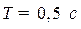

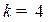Визначити часову характеристику .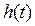

Вирішення.

Маємо характеристичне рівняння:

.

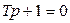Його єдиний корінь 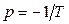. Отже:

.

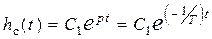Вимушену складову 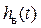будемо шукати у вигляді .

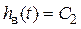Підставивши це рішення у вихідне рівняння, одержимо 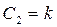. Тоді:

.

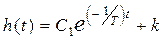Використаємо початкову умову 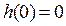. Для цього запишемо рівняння:

.

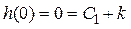Звідки .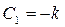

Остаточно одержимо

.

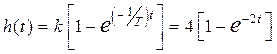Приклад 3.2.

Визначити характеристику 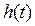для САК із прикладу 3.1 операторним методом.

Вирішення.

Перетворимо по Лапласу вихідне рівняння з урахуванням того, що :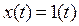

.

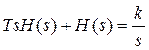Звідки

.

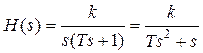Отриманий вираз є дрібно-раціональною функцією, до якої можна застосувати формулу розкладання Хевісайда. Тоді: ; ; .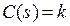

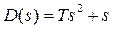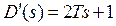Рівняння 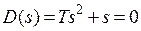має два корен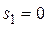і: і .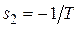

Скориставшись формулою (3.8), остаточно одержимо:

.

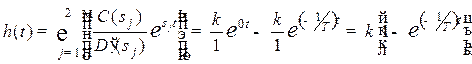Приклад 3.3.

Рівняння САК має вигляд:

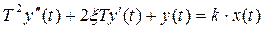
Визначити частотні характеристики при 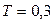с; ; .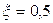

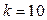Вирішення.

Перетворимо вихідне рівняння по Лапласу при нульових початкових умовах:

.

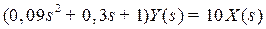Звідки можна одержати вираз для передатної функції:

.

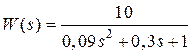Зробивши заміну 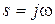, маємо:

.

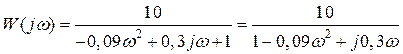Одержимо алгебраїчну форму подання :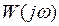

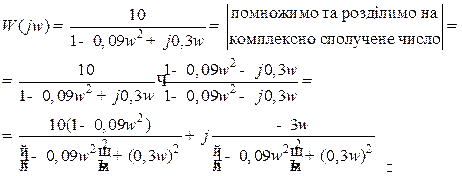
Звідки

; ;

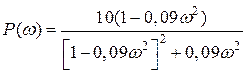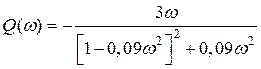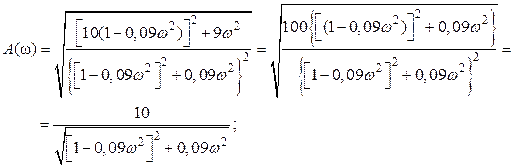
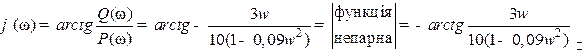
Відповідні графіки представлені на рис. 2.8.

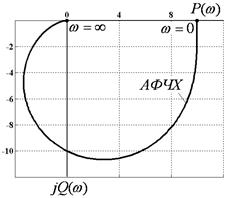
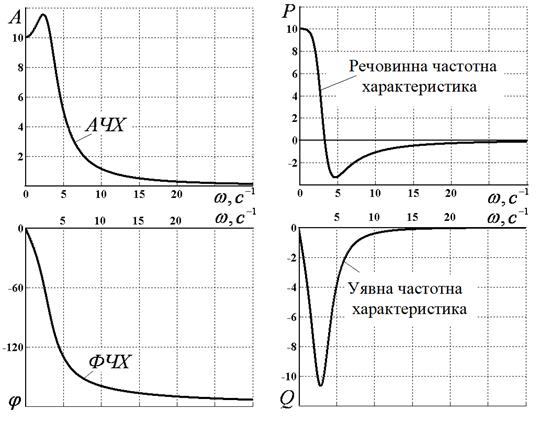
Рис. 2.8

Контрольні запитання

1. Які ви знаєте часові характеристики САК?

2. Які частотні характеристики ви знаєте? Дайте їм визначення.

3. Як експериментально визначити частотні характеристики?

4. Як визначають частотні характеристики по передатній функції?

5.Як будують логарифмічні частотні характеристики?

6. Навіщо вивчають частотні характеристики САК?

7. Як з передатної функції одержати вираз для АФЧХ?

8. Наведіть основні формули, що зв'язують АФЧХ, АЧХ і ФЧХ між собою.

9. Який фізичний зміст мають ординати АЧХ елемента? Як по них оцінити умови пропуску елементом гармонійного сигналу?