Пункт 6. Уравнения в полных дифференциалах

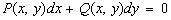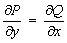Дифференциальное уравнение вида , где , называется уравнением в полных дифференциалах, т.е. левая часть такого уравнения есть полный дифференциал некоторой функции .

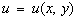Если это уравнение переписать в виде 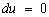, то его общее решение определяется равенством 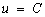. Функция 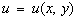может быть найдена по одной из формул:

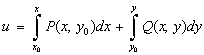
или

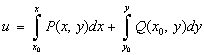
где точка 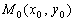принадлежит области определения функций , .

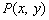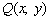Пример:

12.Решить уравнение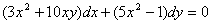

Решение:

Проверим условие тотальности: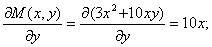

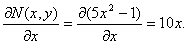
Условие тотальности выполняется, следовательно, исходное дифференциальное уравнение является уравнением в полных дифференциалах.

Определим функцию u.

;

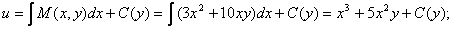
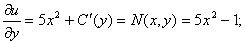
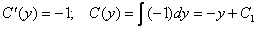Итого,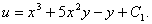

Находим общий интеграл исходного дифференциального уравнения:

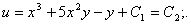
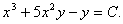
Пункт 7. Дифференциальные уравнения в частных производных.

Примеры

Тема 2.4. Числовые ряды.

Числовой ряд. Основные понятия.

Теоремы и признаки сравнения для положительных числовых рядов.

Знакопеременные ряды.

Степенные ряды. Разложение функций в ряд Маклорена.

Пункт 1. Числовой ряд. Основные понятия.

Рассмотрим произвольную числовую последовательность 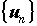и формально составим сумму ее членов 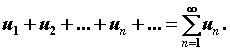Это выражение называют числовым рядом, или просто рядом. Члены последовательности 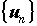называют членами ряда. Конечно, невозможно вычислить сумму бесконечного числа слагаемых, но легко вычислить сумму первых n членов ряда 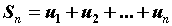. Эта сумма называется n-ой частичной суммой.

Ряд 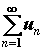называют сходящимся, если существует и конечен предел последовательности 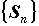частичных сумм ряда. Сам предел при этом называют суммой ряда и обозначают , .

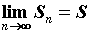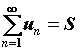Если предел частичных сумм не существует или бесконечен, то ряд расходится.

Разность 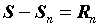называется остатком ряда. Для сходящегося ряда 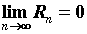. Это означает, что сумму сходящегося ряда можно вычислить с любой точностью, заменяя ее частичной суммой соответствующего порядка. Для расходящегося ряда это не так. Поэтому сходимость или расходимость конкретного ряда является основным вопросом для исследования.

Теорема (необходимое условие сходимости ряда) Если ряд сходится, то .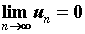

Замечание: Члены ряда могут стремиться к нулю, но ряд при этом может расходиться.

Ряд, вида 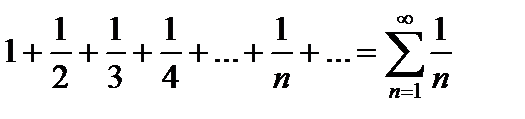называется гармоническим. К сожалению, сказать однозначно, расходится данный ряд или сходится, мы не можем. Для гармонического ряда выполнено необходимое условие сходимости 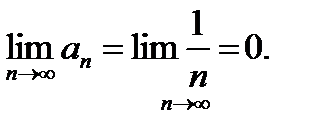Докажем, что этот ряд расходится. Действительно, если бы этот ряд сходился, то, обозначая его сумму через S , мы бы имели:

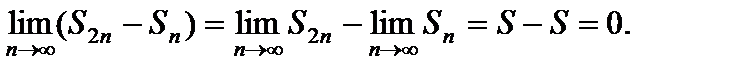Но

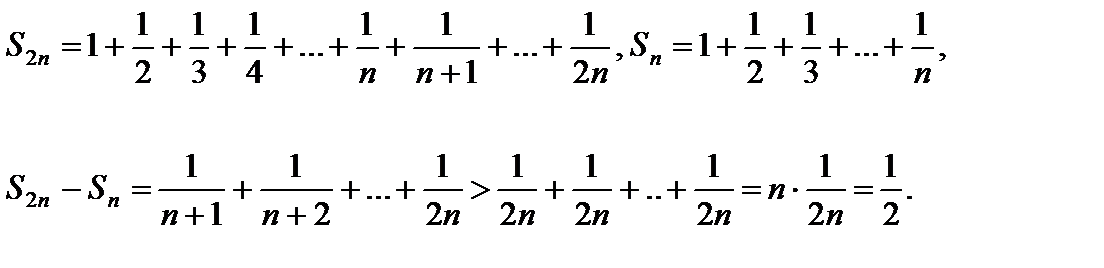
Значит, 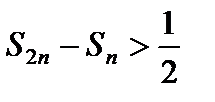. Отсюда следует, что равенство 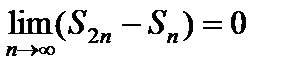невозможно, то есть гармонический ряд расходится.

Замечание.Ряд 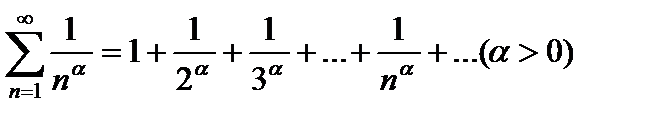называется обобщенным гармоническим рядом илирядом Дирихле. Он сходится при 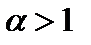и расходится при .

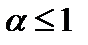Ряд вида 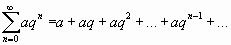называется геометрическим .

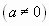Геометрический ряд образован из членов геометрической прогрессии.

Известно, что сумма её первых n членов 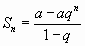. Очевидно: это n-ая частичная сумма геометрического ряда.

Возможны случа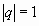и: или 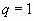. Тогда данный ряд сходится при 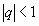и расходится при .

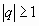Примеры:

1.Найти сумму ряда .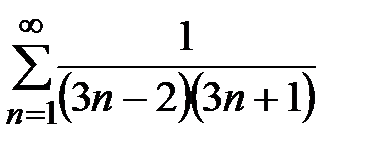

Решение:

Подсчитаем :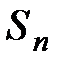

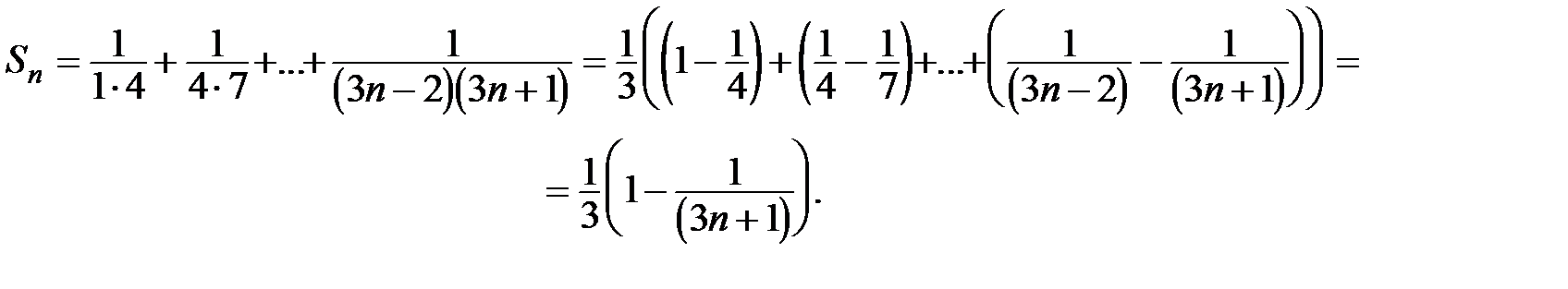По определению .

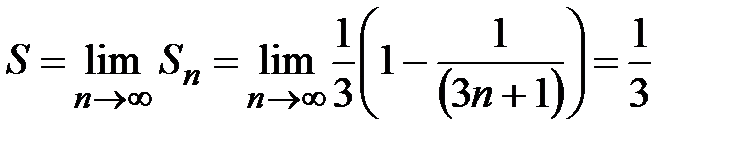2.Найти сумму ряда .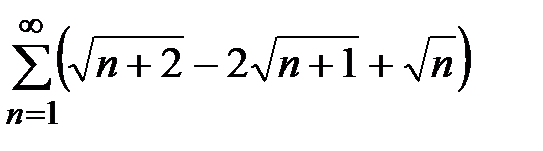

Решение:

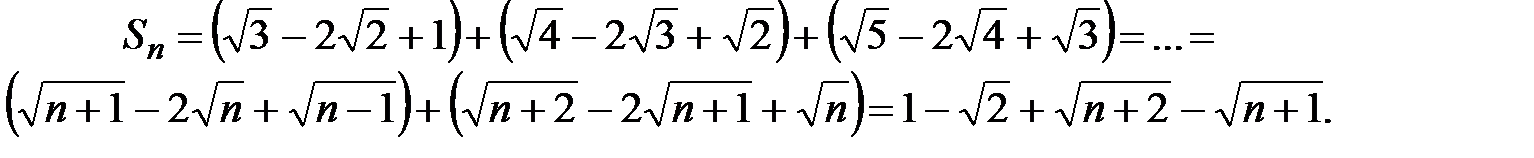
Пользуясь определением суммы ряда и раскрывая неопределённость вида 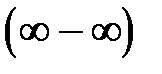, при вычислении предела, получим: