Определённые и неопределённые интегралы

Mathematica может вычислять неопределенные интегралы от простых функций в аналитической (символьной) форме. Для этого используется шаблон или команда Integrate[f,x], где первый параметр означает подынтегральную функцию (она может быть определена заранее с помощью команды f[x_]:=…), а второй - переменную интегрирования; например

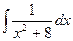
Если подынтегральную функцию определить заранее

:=

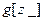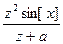
то интеграл вычисляется командой

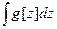
Результат, как видно, содержит специальные функции (интегральный синус и косинус), дифференцированием его можно проверить

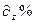
Получившееся в результате дифференцирования сложное выражение можно упростить, восстановив исходный вид подынтегральной функции:

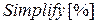
Как известно, не все неопределенные интегралы от элементарных функций можно вычислить в терминах элементарных и специальных функций. Если Mathematica не справляется с вычислением данного интеграла, она оставляет его записанным в "общем виде":

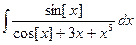
С этим результатом, тем не менее, можно дальше работать, например, дифференцировать:

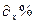
Для вычисления определенных интегралов в команде Integrate надо указать вместе с переменной интегрирования верхний и нижний пределы в виде {x, x_min, x_max}

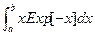
Например

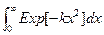
Результат, выданный системой, означает, что при положительности действительной части коэффициента k интеграл существует и равен приведенному выражению, а в противном случае - не существует (расходится).

С помощью опции Assumptions→{} можно указать дополнительные условия, в частности, делающие возможным вычисление интеграла в аналитической форме. Сравните, например

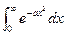и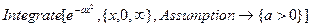

Пределы

Пределы функций можно вычислять с помощью команды Limit[f[x],x→x0], при этом Mathematica умеет раскрывать неопределенности типа 0/0

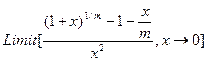
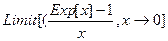
и бесконечность/бесконечность

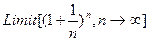
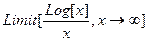
В полученном результате последней операции E=e означает основание натуральных логарифмов.

Однако неопределенности типа бесконечность-бесконечность она не раскрывает и оставляет в "общем виде"

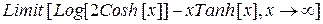
С помощью опции Direction можно вычислять односторонние пределы: снизу

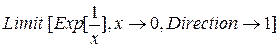
и сверху

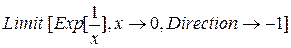
Разложения в ряды

Команда Series[f,{x,x0,n}] осуществляет разложение функции f в ряд Тейлора по переменной x в окрестности x0 до членов степени n по x включительно:

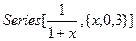
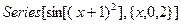
В Out-ячейке O[x]³ обозначает остаточный член ряда. Если его желательно опустить, используйте команду

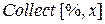
или

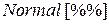
Индивидуальные задания:

1. Вычислить производную:

№	Задание	№	Задание

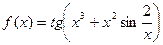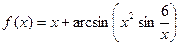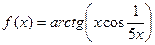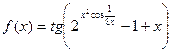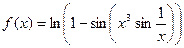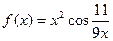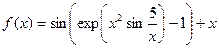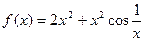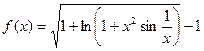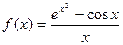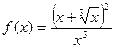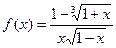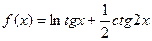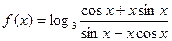2. Вычислить неопределенный интеграл :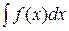

№	f(x)	№	f(x)	№	f(x)

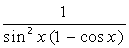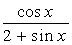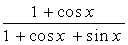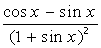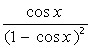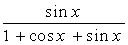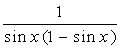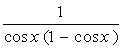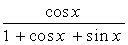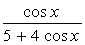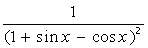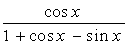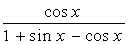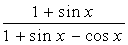3. Вычислить определенный интеграл :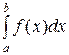

№	f(x)	[a, b]		f(x)	[a, b]
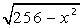		[0, 16]		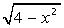	[0, 2]
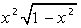		[0, 1]		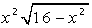	[0, 4]
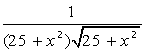		[0, 5]		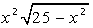	[0, 5]
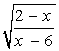		[3, 5]		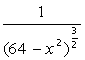	[0,4 ]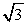
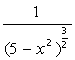		[0, 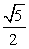]			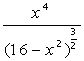[0,2 ]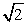
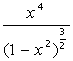		[0, 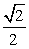]			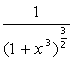[0, ]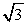
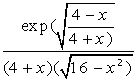		[0, 4]		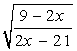	[6, 9]

4. Вычислить предел:

№	Задание	№	Задание

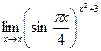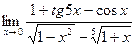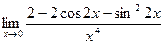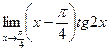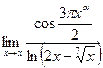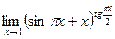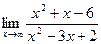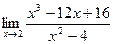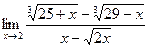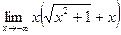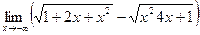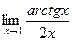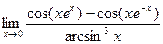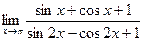5. Разложить функцию f в ряд степени n:

№	функция	n	№	функция	n

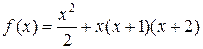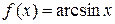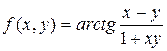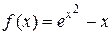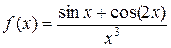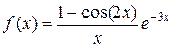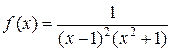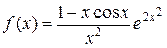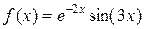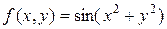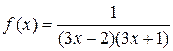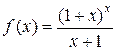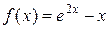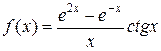Лабораторная работа №4. «Построение графиков в СКМ Mathematica»