Распадающиеся квадратичные формы
Определение 66. Квадратичная форма называется распадающейся, если её можно представить в виде произведения двух линейных форм.
Теорема 70. Квадратичная форма над полем комплексных чисел распадается тогда и только тогда, когда её ранг меньше или равен двум. Квадратичная форма над полем действительных чисел распадается тогда и только тогда, когда либо её ранг не больше единицы, либо её ранг равен двум, а положительный индекс инерции равен единице.
Доказательство. Если форма нулевая (её ранг равен нулю), то утверждение теоремы очевидно. Рассмотрим любую ненулевую форму j(а).
Þ Пусть квадратичная форма j распадающаяся. Тогда
j(а) = (a1х1 + a2х2 + … + anхn)×(b1х1 + b2х2 + … + bnхn).
Возможны два случая:
1. aк = lbк для всех к = 1, 2, … , n. Тогда j(а) = l(a1х1 + a2х2 + … + anхn)2.
Сделав преобразование координат по формулам:
у1 = a1х1 + a2х2 + … + anхn , у2 = х2 , … , уn = хn , получим j(а) = lу12. Но это канонический вид данной формы. Следовательно, ранг формы равен 1.
2. Не все aк равны соответствующим bк .
Сделав преобразование координат по формулам:
у1 = a1х1 + a2х2 + … + anхn , у2 = b1х1 + b2х2 + … + bnхn , у3 = х3 , … , уn = хn , получим
j = у1у2 .
Сделав ещё одно преобразование координат по формулам:
у1 = z1 – z2 , у2 = z1 + z2 , у3 = z3 , … , zn , получим j = z12 – z22. В случае поля действительных чисел это выражение является нормальным видом данной формы. Следовательно, ранг формы равен 2, а положительный индекс инерции равен 1. Если дана форма над полем комплексных чисел, то преобразование у1 = z1 –i z2 , у2 = z1 +i z2 , у3 = z3 , … , zn приводит форму к виду j = z12 + z22. Ранг этой формы равен 2.
Ü Если действительная или комплексная форма имеет ранг 1, то она приводится к нормальному виду j(а) = у12. Из формул преобразования координат у1=a1х1 + a2х2 +…+ anхn . Но тогда j = (a1х1 + a2х2 + … + anхn)2, т.е. форма распадающаяся.
Если комплексная форма имеет ранг 2, то она приводится к виду
j = z12 + z22 = (z1 – i z2)×( z1 +i z2).
Подставив вместо z1 и z2 их выражения из формул преобразования координат, получим в исходных координатах j(а) = (a1х1 + a2х2 + … + anхn)×(b1х1 + b2х2 + … + bnхn), т.е. форма распадающаяся.
Если действительная форма имеет ранг 2 и положительный индекс инерции 1, то она приводится к виду j = z12 – z22 = (z1 – z2)×(z1 + z2). Подставив вместо z1 и z2 их выражения, получим j(а) = (a1х1 + a2х2 + … + anхn)×(b1х1 + b2х2 + … + bnхn), т.е. форма распадающаяся.
Пример. Будет ли распадающейся над полем действительных чисел квадратичная форма: j = 3х12 + 3х1х2 – 2х1х3 + 8х1х4 – 2х2х3 + 5х2х4 – 2х3х4 + 5х42.
Решение. Приведём форму к каноническому виду.
j = 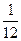 (36х12 + 36х1х2 – 24х1х3 + 96х1х4 + 9х22 + 4х32 + 64х42 – 12х2х3 + 48х2х4 – 32х3х4) –
(36х12 + 36х1х2 – 24х1х3 + 96х1х4 + 9х22 + 4х32 + 64х42 – 12х2х3 + 48х2х4 – 32х3х4) – 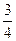 х22 –
х22 –
 –
– 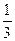 х32 –
х32 – 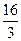 х42 + х2х3 – 4х2х4 +
х42 + х2х3 – 4х2х4 + 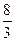 х3х4 – 2х2х3 + 5х2х4 – 2х3х4 + 5х42 =
х3х4 – 2х2х3 + 5х2х4 – 2х3х4 + 5х42 = 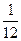 (6х1 + 3х2 – 2х3 + 8х4)2 –
(6х1 + 3х2 – 2х3 + 8х4)2 –
– 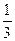 (
( 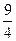 х22 + 3х2х3 – 3х2х4 + х32 + х42 – 2х3х4) +
х22 + 3х2х3 – 3х2х4 + х32 + х42 – 2х3х4) + 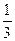 х32 +
х32 + 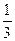 х42 –
х42 – 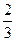 х3х4 –
х3х4 – 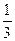 х32 –
х32 – 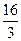 х42 +
х42 + 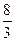 х3х4 –
х3х4 –
– 2х3х4 + 5х42 = 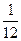 (6х1 + 3х2 – 2х3 + 8х4)2 –
(6х1 + 3х2 – 2х3 + 8х4)2 – 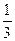 (
( 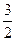 х2 + х3 – х4)2. Отсюда видно, что ранг данной формы равен 2, а положительный индекс инерции равен 1, следовательно, форма распадается. Действительно,
х2 + х3 – х4)2. Отсюда видно, что ранг данной формы равен 2, а положительный индекс инерции равен 1, следовательно, форма распадается. Действительно,
j = 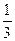 (3х1 +
(3х1 + 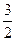 х2 – х3 + 4х4 +
х2 – х3 + 4х4 + 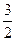 х2 + х3 – х4)×( 3х1 +
х2 + х3 – х4)×( 3х1 + 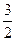 х2 – х3 + 4х4 –
х2 – х3 + 4х4 – 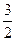 х2 – х3 + х4).
х2 – х3 + х4).
Отсюда j = (х1 + х2 + х4)×(3х1 – 2х3 + 5х4).
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К КОЛЛОКВИУМУ «Определители. Матрицы. Линейные пространства»
1. Метод Гаусса решения системы линейных уравнений.
2. Определители 2-го и 3-го порядка.
3. Перестановки: определение, свойства.
4. Подстановки: определение, свойства.
5. Определители n-го порядка: определение, свойства, в которых говорится о равенстве определителя нулю.
6. Определители n-го порядка: определение, свойства, в которых говорится, что определитель не изменится.
7. Дополнительные миноры и алгебраические дополнения. Вычисление определителя, в котором все элементы одной строки, кроме одного, равны нулю.
8. Теорема о разложении определителя по элементам строки (столбца). Сумма произведений элементов одной строки на алгебраические дополнения элементов другой строки.
9. Теоремы Лапласа и Крамера.
10. Матрицы. Сложение матриц: определение, свойства.
11. Умножение матрицы на элемент поля Р: определение, свойства.
12. Умножение квадратных матриц. Определитель произведения двух матриц.
13. Обратная матрица.
14. Решение матричных уравнений.
15. Определение и примеры линейных пространств.
16. Арифметическое линейное пространство.
17. Линейно зависимые системы векторов: определение, свойства.
18. Линейно независимые системы векторов: определение, свойства.
19. Максимальная линейно независимая система векторов данного линейного пространства: определение, свойства. Максимальная линейно независимая подсистема данной системы векторов. Ранг системы векторов.
20. Базис линейного пространства: определение, примеры, свойства, размерность линейного пространства.
21. Координаты вектора в данном базисе: определение, свойства.
22. Матрица перехода. Связь координат вектора в разных базисах.
23. Подпространства линейных пространств: определение, свойства, примеры. Линейная оболочка системы векторов.
24. Сумма и пересечение линейных подпространств. Теорема о размерности суммы двух конечномерных линейных подпространств. Прямая сумма.
25. Изоморфизм линейных пространств.
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ
1. Комплексные числа: определение; алгебраическая форма, сложение и умножение комплексных чисел, заданных в алгебраической форме; изображение комплексных чисел на евклидовой плоскости; модуль и аргумент комплексного числа; тригонометрическая форма комплексного числа; умножение, деление, возведение в степень и извлечение корня из комплексного числа, заданного в тригонометрической форме.
2. Метод Гаусса решения системы линейных уравнений.
3. Перестановки и подстановки: определение, свойства, чётные и нечётные перестановки и подстановки, умножение подстановок.
4. Определители n-го порядка: определение, свойства; дополнительные миноры и алгебраические дополнения; вычисление определителя, в котором все элементы одной строки, кроме одного, равны нулю. Теорема о разложении определителя по элементам строки (столбца). Сумма произведений элементов одной строки на алгебраические дополнения элементов другой строки. Теоремы Лапласа и Крамера.
5. Матрицы. Сложение матриц: определение, свойства.
6. Умножение матрицы на элемент поля Р: определение, свойства.
7. Умножение квадратных матриц. Определитель произведения двух матриц.
8. Обратная матрица: определение, свойства, способ вычисления.
9. Решение матричных уравнений.
10. Линейные пространства: определение, примеры. Арифметическое линейное пространство. Доказать, что множество матриц одной и той же размерности с элементами из поля Р есть линейное пространство.
11. Линейно зависимые и независимые системы векторов: определение, свойства, примеры.
12. Максимальная линейно независимая система векторов данного линейного пространства: определение, свойства. Максимальная линейно независимая подсистема данной системы векторов. Ранг системы векторов.
13. Базис линейного пространства: определение, примеры, свойства, размерность линейного пространства. Размерности арифметического линейного пространства, пространства матриц и пространства многочленов R[х].
14. Координаты вектора в данном базисе: определение, свойства. Действия с векторами в координатах. Матрица перехода. Связь координат вектора в разных базисах.
15. Подпространства линейных пространств: определение, свойства, примеры. Линейная оболочка системы векторов.
16. Сумма и пересечение линейных подпространств. Теорема о размерности суммы двух конечномерных линейных подпространств. Прямая сумма.
17. Изоморфизм линейных пространств: определение, свойства, примеры.
18. Столбцовый и строчный ранги матрицы: определение, теорема о столбцовом ранге матрицы, ранг матрицы, практическое правило вычисления ранга матрицы.
19. Теорема Кронекера-Капелли о системе линейных уравнений. Практическое правило решения системы линейных уравнений, общее и частное решения.
20. Пространство решений системы линейных однородных уравнений, фундаментальная система решений (ФСР), выражение общего решения через ФСР.
21. Связь решений системы линейных неоднородных уравнений и соответствующей системы линейных однородных уравнений.
22. Задание подпространств конечномерного линейного пространства с помощью систем линейных уравнений.
23. Линейные операторы: определение, примеры, свойства, сумма линейных операторов, умножение линейного оператора на элемент основного поля.
24. Матрица линейного оператора в данной паре базисов. Соответствие между всеми линейными операторами j : Ln ® Lm и всеми матрицами порядка n´m с элементами из основного поля.
25. Теорема о задании линейного оператора j : Ln ® Lm базисом из Ln и упорядоченным набором n векторов из Lm .
26. Связь между координатами вектора и его образа при линейном операторе. Связь между матрицами линейного оператора в разных парах базисов.
27. Область значений и ядро линейного оператора: определение, свойства, примеры.
28. Линейные преобразования линейного пространства: определение, примеры, свойства.
29. Сумма линейных преобразований, умножение линейного преобразования на элемент поля Р. Линейное пространство, сопряжённое данному линейному пространству.
30. Собственные векторы и собственные значения линейного преобразования: определение, примеры, свойства.
31. Характеристический многочлен, характеристические корни и собственные значения квадратной матрицы.
32. Нахождение собственных значений и собственных векторов линейного преобразования.
33. Линейные преобразования в базисе из собственных векторов. Линейные преобразования с простым спектром.
34. Скалярное произведение векторов, его свойства. Определение и примеры евклидовых и унитарных пространств.
35. Матрица Грама в евклидовом пространстве: определение, свойства, формула для вычисления скалярного произведения.
36. Длина вектора, угол между векторами, ортогональность векторов в евклидовом пространстве: определение, примеры, свойства.
37. Ортогональные дополнения вектора и евклидова подпространства: определение, свойства, примеры.
38. Ортонормированные базисы в евклидовом пространстве: определение, свойства, примеры. Теорема о том, что любой базис в конечномерном евклидовом пространстве можно ортонормировать. Скалярное произведение векторов, заданных координатами в ортонормированном базисе.
39. Изоморфизм евклидовых пространств: определение, свойства, примеры.
40. Ортогональное линейное преобразование: определение, примеры, свойства. Ортогональная матрица.
41. Сопряжённые линейные преобразования: определение, свойства, примеры. Доказать, что для всякого линейного преобразования пространства Еn существует сопряжённое.
42. Самосопряженные (симметрические) линейные преобразования: определение, примеры, свойства. Симметрические матрицы, их свойства.
43. Билинейные формы.
44. Квадратичные формы: определение, примеры. Матрица квадратичной формы. Матричная запись квадратичной формы. Канонический и нормальный вид квадратичной формы. Теорема о приведении квадратичной формы к каноническому и нормальному виду над полем R (над полем С).
45. Приведение квадратичной формы к каноническому виду с помощью выделения полных квадратов.
46. Ранг, положительный индекс инерции, дефект действительной и комплексной квадратичных форм. Закон инерции квадратичной формы.
47. Положительно определённые квадратичные формы: определение; необходимое и достаточное условие, при котором форма является положительно определённой; примеры.
48. Распадающиеся квадратичные формы: определение; необходимые и достаточные условия, при которых форма является распадающейся над полем R (над полем С).
ЛИТЕРАТУРА
ОСНОВНАЯ ЛИТЕРАТУРА
1. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, 1974 (и все последующие издания ).
2. Половицкий Я.Д. Алгебра. Части 1 и 2. – Пермь: ПГУ, 2010.
3. Шевцов Г.С. Линейная алгебра: теория и прикладные задачи. – М: Финансы и статистика, 2003.
4. Курош А.Г. Курс высшей алгебры. – М.: Физматгиз, 1959 ( и все последующие издания).
5. Шевцов Г.С. Линейная алгебра. – Пермь, ПГУ, 1996.
6. Проскуряков И.В. Сборник задач по линейной алгебре. – М.: Наука, 1984 (и все последующие издания)
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Беклемышев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Физматгиз, 2000.
2. Шилов Г.Е. Введение в теорию линейных пространств. М.: Наука, 1984.
МЕТОДИЧЕСКАЯ ЛИТЕРАТУРА
1. Линейная алгебра. Лабораторные работы 1 – 7 и 8 – 13. – Пермь: ПГУ, 2006.
2. Методические указания к лабораторным работам по алгебре и геометрии. – Пермь: ПГУ, 1984.
