Общая теория линий влияния

Понятие о линиях влияния.

Построение линий влияния для простых балок

Принцип независимости действия сил позволяет расчленять на­грузку на отдельные части и вести расчет порознь на действие каж­дой из них. Простейшей базовой нагрузкой является единичная со­средоточенная сила, приложенная в определенной точке и в опре­деленном направлении. Из сосредоточенных сил можно получить любую нагрузку, в том числе и распределенную, путем предельного перехода к бесконечной сумме бесконечного числа сосредоточен­ных сил. Поэтому имея расчет системы на действие единичной со­средоточенной силы, приложенной в произвольной точке и по про­извольному направлению, мы сможем легко рассчитать систему и на любую нагрузку. Данный подход является аналогом известного метода функций Грина из математики.

При перемещении точки приложения сосредоточенной силы усилие в рассматриваемом сечении системы, естественно, изменяет­ся. График, изображающий закон изменения усилия или дефор­мационного фактора в данном сечении в зависимости от положения на сооружении единичного груза Р =1, называется линией влия­ния.

Точно также можно определить линию влияния какого-либо пе­ремещения, например прогиба в определенной точке, от действия единичной сосредоточенной нагрузки, приложенной в различных местах системы.

Линии влияния главным образом применяют в балочных систе­мах (а также в арках, фермах и других стержневых системах), в которых сосредоточенная сила может переме­щаться вдоль проле­та, сохраняя свое направление. При помощи линий вли­яния легко рассчи­тать балку на подви­жную нагрузку, возникающую, например, при движении поезда или потока автомашин на мостовом пролете.

Нетрудно построить линии влияния усилий в простых статиче­ски определимых балках. Опорные реакции балки (рис. 1) при единичной сосредоточенной силе, приложенной на расстоянии х от левой опоры, равны:

SМ_В = 0; R_А×l – P (l–х) =0;

где l — пролет балки.

Отсюда: R_А= P (l–х)/ l – уравнение прямой л.в. R_А.

SМ_А = 0; R_В×l – Рх =0;

Отсюда: R_В = Рх/ l уравнение прямой л.в. R_В.

На консольных участках л.в. R_А и R_В можно получить из л.в. для балки без консоли; надо только продолжить прямую, ограничивающую л.в., до пересечения с вертикалью, проходящей через конец консоли (рис. 1).

Каждая линия влияния дает представление об изменении только того фактора, для которого она построена.

Линию влияния необходимо отличать от эпюры. Это по существу противоположные друг другу понятия. Действительно, ординаты эпюры характеризуют распределение изучаемого фактора по различным сечениям при неподвижной нагрузке; ординаты же линии влияния, наоборот, характеризуют изменение фактора, возникающего в одном определенном сечении при силе Р=1, перемещающейся по длине балки.

R_А Р=1 R_В

х

А В

k l

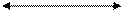
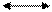
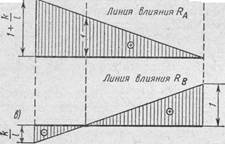
Рис. 1. Л.в. опорных реакций

в простой двухопорной балке

с левой консолью

Для сечений, расположенных слева от точки приложения сил (а < х), изгибающий момент М₁ = R_A × а, а для сечений, располо­женных справа от этой точки (а > х), М₁ = R_B (l - а)= R_B×в.

Следовательно, линию влияния изгибающего момента в сечении, расположенном на расстоянии а от левой опоры однопролетной балки, описывает график функции М₁= х×а/ l(правая прямая л.в.М₁).

При х = 0 М₁ = 0;

при х = l М_{1 =} а.

Построим левую прямую л.в. М₁. Пусть Р=1 находится левее сечения 1, тогда М₁ = 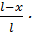в левая прямая л.в. М_1.

Откуда следует, что линия влияния имеет вид треугольника с вершиной в заданном сечении1 (рис. 2).

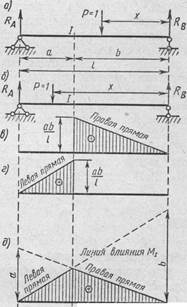
Рис. 2. Построение л.в. М₁

Линия влияния изгибающего момента в консольной балке для сечения «к», расположенного на расстоянии в от свободного конца (рис. 3), выражается формулами:

М_к = 0, когда Р=1 находится левее сечения «к»;

М_к = – в, когда Р=1 находится на участке а < х≤ в.

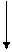х

Р=1

к

а в

l

Л.в. М_к Рис 3. Построение л.в. М_к

и Q_к в консольной балке

-–

в

Л.в. Q_к

1

Для консольных балок строим только л.в. изгибающего момента и поперечных сил, так как л.в. опорной реакции R_A не зависит от положения единичной силы и все ее ординаты равны +1.

Рассмотрим способы построения линий влияния поперечных сил для простой балки(рис. 4).

Л.в. Q_к строим в два этапа:

1) Р=1 находится левее сечения «к», тогда

Q_к = – R_В = – х/l – левая прямая;

2) Р=1 находится правее сечения «к», тогда

Q_к = R_А= (l–х)/ l – правая прямая.

R_А х Р=1 R_В

А к

В

а в

l

а/l л.в. Q_к

в/l 1

Рис. 4. Построение л.в. Q_к

Определение усилий и перемещений в статически определимых стержневых системах при неподвижной и подвижной нагрузках

Усилие S (рис. 5) от нагрузки (от сосредоточенных сил) может быть определено по формуле:

S = P₁h₁ + P₂h₂ + P₃h₃ + • • • + P_nh_n = SP_i h_i.

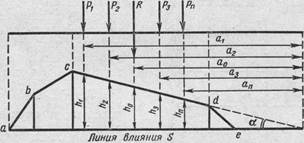
Рис.5. Определение усилия по л.в.

Если на инженерное сооружение действует распределенная нагрузка интенсивностью q и есть линия влияния какого-либо усилия S (рис.6), то это усилие может быть определено по формуле:

S = qw, где w – площадь, ограниченная линией влияния под загруженным участком.

q

л.в. S

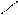
w

Рис. 6

ОПРЕДЕЛЕНИЕ НЕВЫГОДНЕЙШЕГО ПОЛОЖЕНИЯ НАГРУЗКИ НА СООРУЖЕНИИ

Выше было показано, каким образом при помощи линий влияния определяются различные усилия (например, опорная реак­ция, изгибающий момент, поперечная сила и т. д.) от нагрузки, расположе­ние которой задано. Теперь покажем, как надо расположить заданную на­грузку на сооружении, чтобы она вызвала наибольшее значение рассматрива­емого усилия. Такое положение нагрузки называется н е выгоднейшим, или опасным.

Будем в дальнейшем наибольшие положительные усилия обозначать max S, max М, max Q и т. д., а наибольшие по абсолютной величине отрицатель­ные усилия min S, min М, min Q и т. д.

1. Случай действия на сооружение одного сос­редоточенного подвижного груза. Задача отыскания наи­большей величины искомого усилия S в этом случае решается особенно прос­то: опасным является расположение груза над наибольшей ординатой линии влияния. Умножив величину груза на эту ординату, получим наибольшее значение искомого усилия. При отыскании максимума усилия берется зна­чение наибольшей положительной ординаты, а при отыскании минимума — значение наибольшей по абсолютной величине отрицательной ординаты линии влияния.

2. Случай действия на сооружение любой связанной системы подвижных грузов (рис.7).

S = SP_i h_i.

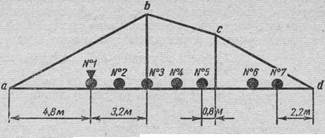
Рис. 7

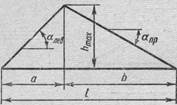
Рис. 8

Переход от случая, когда нагрузка расположена чуть правее, чем это показано на рис. 7, к случаю когда она расположена чуть левее, связан с изменением знака рассматриваемой суммы от отрицательного к положительному. Сле­довательно, расположение нагрузки, пока­занное на рис. 7, является опасным. Критическим грузом является груз № 3.

Рассмотрим, что было бы, если бы вели­чина каждого из грузов № 8 и 9, расположенных в найденном опасном положении за пределами линии влияния (справа от нее), значительно превышала ве­личины остальных грузов (например, равня­лась бы 15 тс). В этом случае при дальней­шем перемещении нагрузки влево от опасного положения, когда грузы №8 и 9 расположились бы на участках bс и cd линии влияния, сумма стала бы снова отрицательной, а затем (когда один из этих грузов переместился бы за вершину b линии влияния) снова положительной. Таким образом, имело бы место второе опасное положение нагрузки, для которого было бы получе­но второе значение шах S. Расчетным бы явилось большее из двух найденных значений max S.

Рассмотрим теперь вопрос об определении опасного положения нагрузки при линии влияния, имеющей вид треугольника (рис. 8).

Часто заданная подвижная нагрузка (например, нагрузка от паровоза) может въезжать на сооружение (пролетное строение моста) как слева напра­во, так и справа налево. Каждому из этих случаев соответствует свое значе­ние шах 5 усилия S. Для получения большего из них следует передние гру­зы паровоза (обычно наиболее тяжелые) располагать слева в случаях, когда а < b (см.рис. 8), и справа, — когда а > 6.