Умножение и деление на сопряженное выражение

Примеры:

1. Найти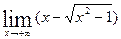

Решение:

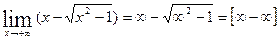- неопределенность, для раскрытия её требуется домножить на сопряжённое выражение, т.е :

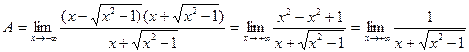Вычислим предел: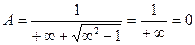

Ответ: 0.

2. Найти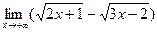

Решение:

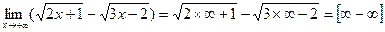- неопределенность, для раскрытия её необходимо домножить на сопряженное выражение:

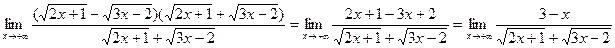
Вычислим предел:

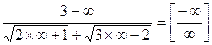- неопределенность, для её раскрытия необходимо сократить дробь на наивысшую степень переменной x:

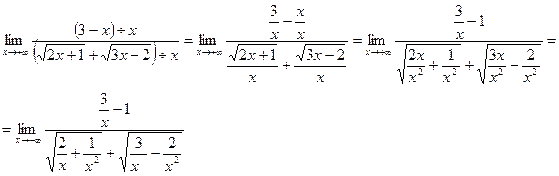
Вычислим предел:

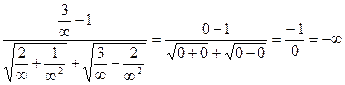
Ответ: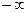

3.3. Неопределенность вида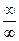

Деление на наибольшую степень

Предел отношения двух многочленов (при условии, что аргумент стремится к ∞) равен пределу отношения их старших членов.

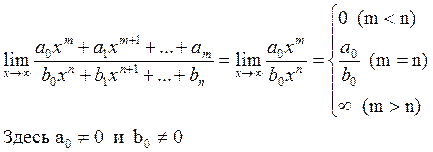
Примеры:

1. найти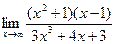

Решение:

Имеем неопределённость вида 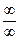. Для раскрытия неопределённости разделим почленно числитель и знаменатель на наивысшую степень x, т.е. на x³, предварительно раскрыв скобки.

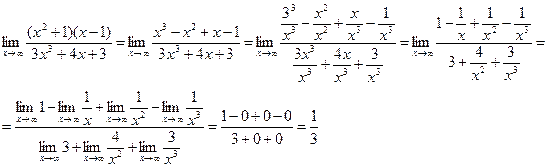
Ответ: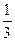

2. Найти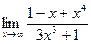

Решение:

Имеем неопределённость вида 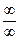. Для раскрытия неопределённости разделим почленно

числитель и знаменатель на наивысшую степень x, т.е. на x⁴ .

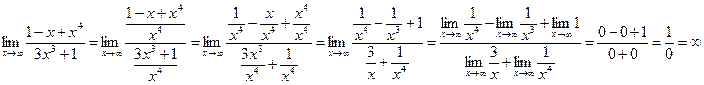Ответ: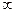

Замена переменной

Пример:

Найти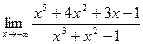

Решение:

Имеем неопределённость вида 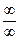. Для раскрытия неопределённости сделаем замену x=−t (t=-x, t→+∞ при x→−∞), а затем разделим почленно числитель и знаменатель на наивысшую степень t, т.е. на t⁵.

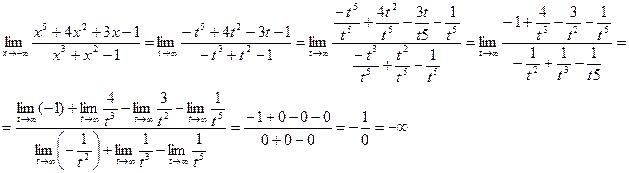Ответ: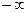

3.4. Неопределенность вида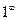

Применение второго замечательного предела

;

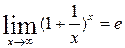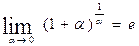
Пример:

Найти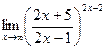

Решение:

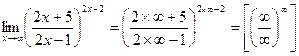- неопределенность.

Т.к 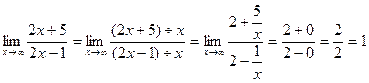, то неопределенность вида .

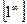Для ее раскрытия применим 2-й замечательный предел: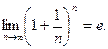

а) Выделим из дроби 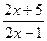целую часть:

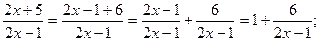
а) заменим 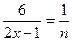, чтобы дробь 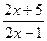приняла вид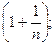

в) для выражения предела А через новую переменную «n» необходимо найти (2x-2) и выяснить к какому значению стремится «n»:

Т.к 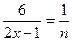, то 2x-1=6n и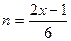

2x=6n+1

2x-2=6n+1-2

2x-2=6n-1

Т.к 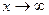, то n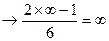

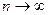
Т.о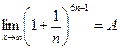

г) Разложим данный предел по свойствам предела и степени:

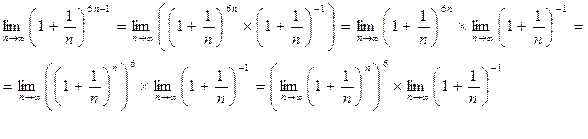и вычислим предел

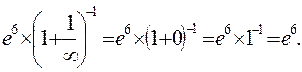
Ответ: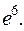

3.5. Неопределенность вида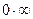

Сведение данной неопределенности с помощью равносильных преобразований к неопределенностям вида 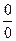или .

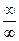Пример.

Найти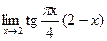

Решение:

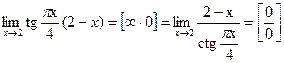
Применим правило Лопиталя

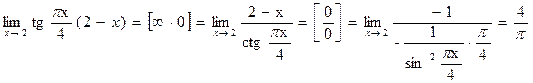
Ответ.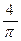

IV. АСИМПТОТЫ КРИВОЙ

Прямая называется асимптотой кривой y=f(x), если расстояние от точки М(x;y) до этой прямой стремится к 0 при стремлении хотя бы одной из координат к ∞

Вертикальные асимптоты.

График функци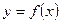и при 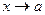имеет вертикальную асимптоту, ес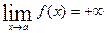ли или 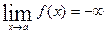; при этом точка 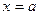есть точка разрыва II-го рода. Уравнение вертикальной асимптоты имеет вид .

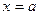Горизонтальные асимптоты.

График функци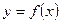и при 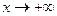или при 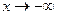имеет горизонтальную асимптоту, ес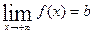ли или 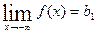. Может оказаться, что либо только один из этих пределов конечный, либо ни одного. Тогда график имеет или одну горизонтальную асимптоту, или ни одной. Уравнение горизонтальной асимптоты имеет вид 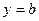(рис. 9).

Рис. 9. Графики функций, имеющие горизонтальные асимптоты

Наклонные асимптоты.

Если существуют пределы 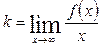и 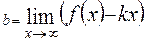, то прямая y=kx+b является наклонной асимптотой кривой при указанном стремлении x. При x→ 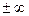асимптоты могут быть различны.