Некоторые свединия из векторной алгебры

Величины, требующие для своего задания не только указания числового значения, но и направления в пространстве, называют­ся векторными величинами или векторами [6] .

Для наглядного изображения векторов служат геометрические векторы- прямолинейные отрезки, имеющие определенную длину и направление и обозначаемые буквой с чертой /например, /.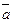

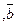Длина вектора 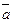называется модулем /скаляром, абсолютной величиной/ и обозначается как 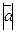или a.

Вектор 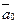, который имеет длину, равную единице, называ­ется единичным вектором или ортом, причем .

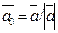Пространственная система координат вполне определяется выбором начала координат и ортов 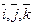трех взаимно перпендикулярных осей координат.

Система координат называется правой, если из конца вектора 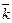кратчайший путь для совмещения вектора 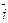с вектором 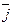наблюдается как поворот вектора 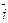против направления движе­ния часовой стрелки.

Любой вектор 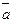может быть разложен по трем некомпланар­ным /не лежащим в одной плоскости/ векторам 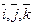,причем 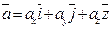. Коэффициенты а_х, a_y, a_z этого разложения называются координатами вектора .

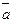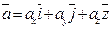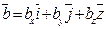Если даны два вектора и . то суммой /разностью/ этих векторов называется .

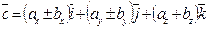Скалярным произведением двух векторов 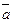и 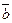называется произведение длин этих векторов на косинус угла между ними:

.

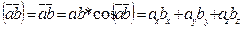Векторным произведением двух векторов 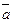и 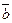называется вектор 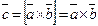обладающий следующими свойствами:

1) длина вектора 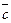равна площади параллелограмма, построен­ного на векторах 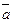и 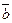, то есть ,

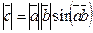2) вектор 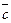перпендикулярен векторам 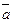и ,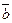

3) вектора 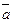, , 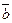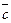- составляют правую тройку векторов.

Векторное произведение в координатной форме представляется в следующем виде: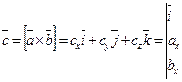

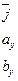
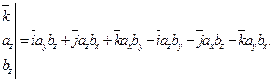
ЛИТЕРАТУРА

Основная

1. Дарков А.П., Шпиро Г.Г. Сопротивление материалов, м.: Высшая школа. 1969. 734 с.

2. Гибшман М.Е. Ппименение векторного анализа к расчету геометрических характеристик сечений строительных конструкций // Известия пупов. Строительство и архитектура. № 2, 1971.

С. 52-57.,

3. Кузнецов О.Р., Кривошеий И.В. Вычисление геометрических характеристик плоских сечений с помощью ЭВМ: Метод, указ. /Сарат. политехн, ин-т . Саратов, 1986. 28 с.

Дополнительная

4. Реконотцукпия промышленных предприятий, т..1 / Под ред. Топчия В.Д., Гребенника Р.А. М.: Стройиздат, 1990. 591 с.

5. Рекомендации по учету влияния дефектов и повреждений на эксплуатационную пригодность стальных конструкций произ­водственных зданий. М., 1987. 46 с.

6. Бронштейн И.Н., Семендяев К.А. Справочник по математике. М.: Наука. 1986 544 с.

СОДЕРЖАНИЕ

Введение...........................................................................................................................3

Цель работы.......................................................................................................................4

Задание на работу..............................................................................................................4

Технические и языковые средства выполнения работы………………………………………..5

Теоретическая часть……………………………………………...............................................5

Иллюстративные примеры ...............................................................................................10

Порядок выполнения работы……………………………………………………………………19

Содержание и оформление отчета о работе……………………………………………………20

Контрольные вопросы……………………………………………………………………………20

Варианты заданий.............................................................................................................21

Программа расчета геометрических характеристик

поперечных сечений с учетом движения фронта повреждения ………………………………24

Схема алгоритма................................................................................................................26

Бланк-задание....................................................................................................................27

Контрольный пример ........................................................................................................27

Приложение……………………………………………………………………………………….30

Литература.........................................................................................................................31