Дифференцирование функции одной переменной. Исследование функций с помощью производной
Типовой расчёт № 5
Образец выполнения типового расчёта
Задание 1. Вычислить приращение функции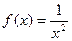 
в точке 
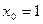, соответствующее приращению аргумента 
.
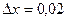Решение:
Воспользуемся формулой: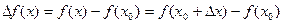 
. Для данной функции получим: 
.
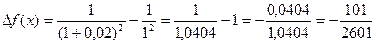Ответ: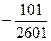 
.
Задание 2. Найти производные функций:
2.1.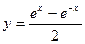 
Решение:
.
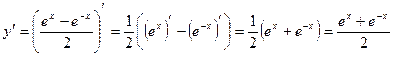. 2.2.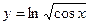 
.
Решение:
Используем правило дифференцирования сложной функции: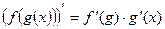 
.
.
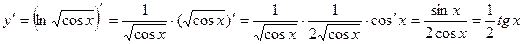Заметим, что этот результат можно было получить, представив функцию в виде 
.
2.3.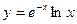 
.
Решение:
Воспользуемся правилом дифференцирования произведения двух функций: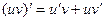 
. Получим 
.
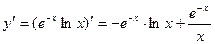2.4.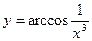 
.
Решение:
Снова используем формулу производной сложной функции: 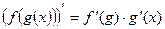. Получим: 
.
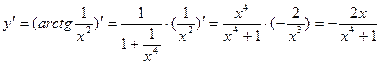Задание 3. Продифференцировать неявно заданную функцию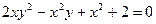 
.
Решение:
Продифференцируем обе части данного уравнения по переменной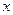 
, учитывая при этом, что 
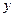является функцией аргумента 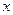. Получим:
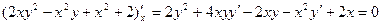. Из полученного равенства выразим производной 
: 
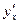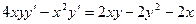, откуда 
.
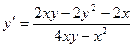Задание 4. Продифференцировать функцию, заданную параметрически:
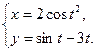
Решение:
Используем правило дифференцирования функции, заданной параметрически: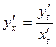 
. Получим: 
.
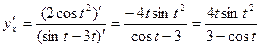Задание 5. Вычислить с помощью дифференциала приближённое значение выражения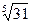 
.
Решение:
Используем приближённое равенство: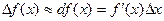 
, верное при малых значениях 
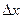. Откуда: 
.
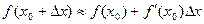Преобразуем сначала исходное выражение: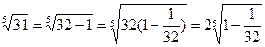 
. Положим 
, , 
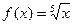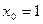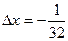. Производная равна: 
, 
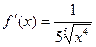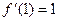. Окончательно имеем: 
.
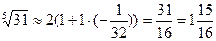Задание 6. Найти вторую производную функции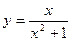 
.
Решение:
Сначала находим первую производную: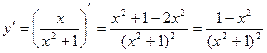 
.
Вычисляем вторую производную: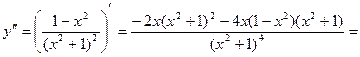 
.
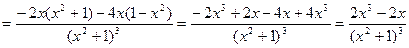Задание 7. Составить уравнения касательной и нормали к графику функции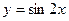 
в точке 
.
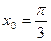Решение:
Запишем уравнение касательной: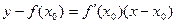 
. В нашем случае 
, 
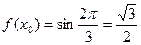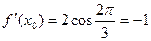. Подставляем в уравнение: 
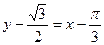, откуда 
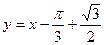- уравнение касательной.
Запишем уравнение нормали: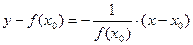 
. Подставив в это уравнение числовые данные: 
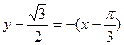, откуда 
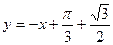- уравнение нормали.
Задание 8. Найти производную функции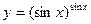 
с помощью логарифмического дифференцирования.
Решение:
Запишем общую формулу логарифмической производной: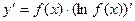 
. В нашем случае: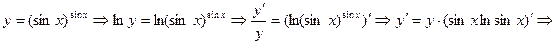 
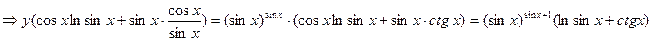Задание 9. Исследовать функцию и построить ее график:
а)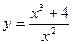 
Решение.
1. Находим область определения.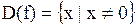 
.
2.Исследуем на четность.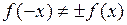 
, следовательно функция общего вида.
3. Находим точки пересечения с координатными осями: c осью Ох: y = 0; x =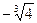 
с осью Оу: x = 0; y – не существует.
4. Исследуем на непрерывность. Функция определена и непрерывна при всех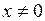 
. х=0 – точка разрыва. 
.
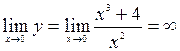5. Найдем асимптоты графика функции.
Так как в точке х=0 функция имеет бесконечный разрыв, то прямая х = 0 является вертикальной асимптотой.
Наклонные асимптоты ищем в виде: y = kx + b.
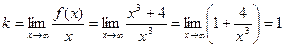
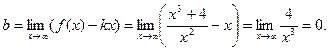
Наклонная асимптота у = х.
6. Находим интервалы монотонности функции и точки экстремума.
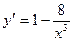; y¢ = 0 при х = 2, у¢ = ¥ при х = 0.
Стационарная критическая точка: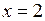 
.
Составим таблицу:
| х | (- 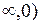  | (0,2) | (2,+  | ||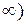
 | + |  | - | + | |
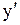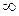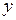 | возрастает | Не сущ. | убывает | возрастает |
Таким образом, точка (2, 3) является точкой минимума.
Экстремум функции: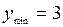 
.
7.Находим интервалы выпуклости и точки перегиба графика функции.
Находим вторую производную.
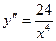> 0 при любом х ¹ 0, следовательно, функция вогнутая на всей области определения.
8. Построим график функции.
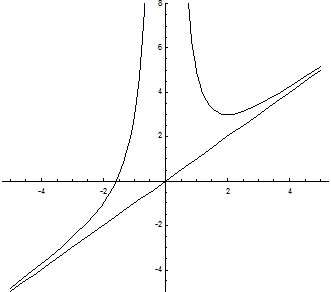
В)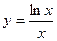 
Решение.
1. Находим область определения.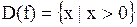 
.
2. Исследуем на четность. 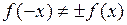, следовательно функция общего вида.
3. Находим точки пересечения с координатными осями: c осью Ох: y = 0; x = 1
с осью Оу: x = 0; y – не существует.
4. Исследуем на непрерывность. Функция определена и непрерывна в интервале (0;+¥). В граничной точке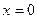 
области определения функция имеет бесконечный разрыв, так как 
.
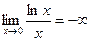5. Так как в точке 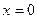функция имеет бесконечный разрыв, то прямая 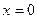является вертикальной асимптотой.
Найдем уравнение наклонной асимптоты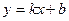 
.
.
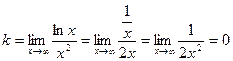Так как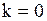 
, то наклонных асимптот нет.
.
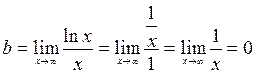(При нахождении пределов воспользовались правилом Лопиталя).
Итак,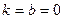 
и уравнение горизонтальной асимптоты 
.
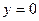Таким образом, график имеет в качестве асимптот оси координат.
6. Находим интервалы монотонности функции и точки экстремума.
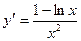. y¢ = 0 при х =е. Стационарная критическая точка: 
.
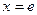Исследуем знак производной на интервалах(0;е) и (е;¥).
Составим таблицу:
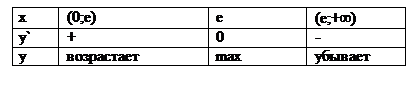
Экстремум функции: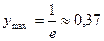 
.
7.Находим интервалы выпуклости и точки перегиба графика функции.
Найдем вторую производную и значения х, при которых график может иметь точку перегиба:
, 
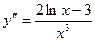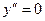при 
.
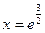Определим знак второй производной в интервалах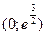 
и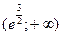 
|
|
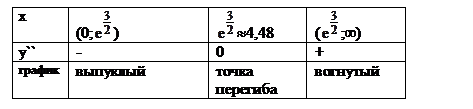
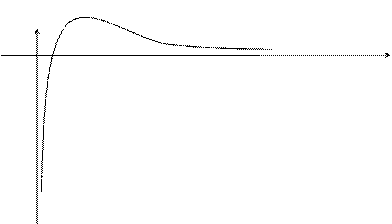
Составим таблицу:
y(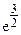 
)=3/(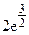 
) » 0,33
8. Построим график функции.
|
 | |||
| |||
Задание 10. Найти наибольшее и наименьшее значение функции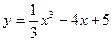 
на отрезке 
.
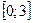Решение:
Найдём область определения функции: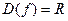 
. Далее, продифференцируем функцию: 
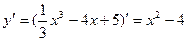. Найдём критические точки: 
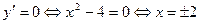. Одна из них, 
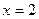, принадлежит рассматриваемому промежутку. Определим значение функции в границах отрезка и в этой точке:
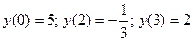. Таким образом, 
.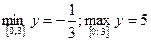