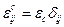Уравнения Максвелла в среде без учёта пространственно-временной дисперсии

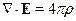
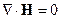
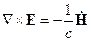
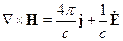
С помощью этих уравнений можно описывать электромагнитное поле в среде. В среде будем ставить индекс « 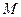»=микро

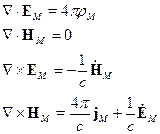
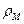включает в себя как связанные, так и свободные заряды в веществе. Каждой точке пространства ставится в соответствие функция 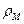. Это значит, что мы заменяем реальную среду моделью – сплошной средой, т.е. мы свойства разных точек «размазываем» по пространству. Существуют следующие способы описания сплошной среды на основе реальной среды:

1. Усреднение по некоторому физическому объёму 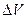и времени .

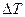2. Статистическое усреднение. Считаем что у нас есть макроскопически-идентичный ансамбль систем(т.е. все внешние условия одинаковы). Здесь производятся измерения для отдельных ансамблей, а потом происходит усреднение. Этот способ более предпочтителен.

Усреднение будем обозначать символами «< >». Отметим, что усреднение коммутативно с дифференциальными операторами.

Итак, усредняем:

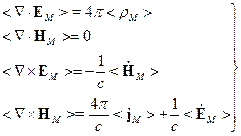
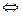
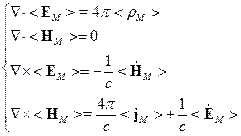
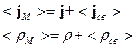
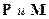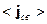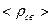Среда под действием внешнего электромагнитного поля поляризуется, т.е. реагирует на внешнее воздействие. В случае, когда отсутствует пространственная дисперсия, поляризация характеризуется векторами электрической и магнитной поляризации . Можно показать, что и выражаются через :

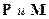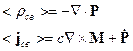
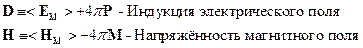
Введём обозначения: ;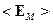

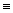
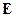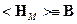
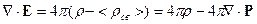
Перенесём второе слагаемое из правой части в левую и объединим его с :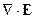

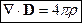
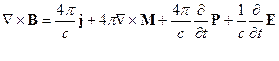
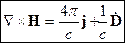
Итак, уравнения Максвелла для среды имеют вид:

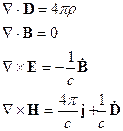
Теорема Стокса.

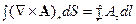- теорема Стокса

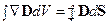
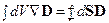
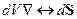- Теорема Гаусса в операторной форме

Например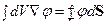

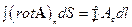
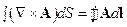
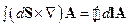
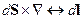- теорема Стокса в операторной форме.

Задачи

1. Пользуясь теоремой Остроградского-Гаусса, вычислить интегралы:

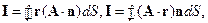
если объем, который охватывает замкнутая поверхность, равен V; A –постоянный вектор.

Решение. Умножим искомый интеграл на постоянный вектор р:

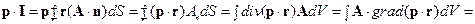
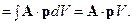
Так как вектор рпроизволен, то

.

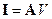Аналогично показывается, что

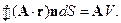
Функциональные соотношения различных полей

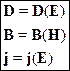
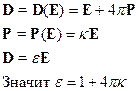
Здесь 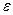- диэлектрическая проницаемость, а 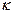- диэлектрическая восприимчивость.

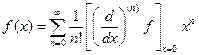-разложение функции 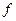в ряд Маклорена.

Если же :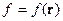

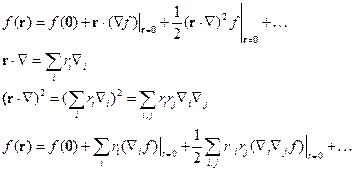
Возможно разложить 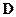по векторам 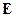в ряд Маклорена:

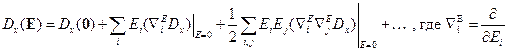
Первое слагаемое – это индукция, связанная с собственным дипольным моментом в отсутствие внешнего поля (собственная поляризация) – пироэлектрики.

Второе слагаемое – линейные среды.

Третье слагаемое – учёт нелинейности среды.

Среды, для которых нелинейные члены в разложении индукции по полю имеют вес, называются нелинейными.

Линейные среды

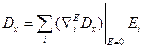
Введём обозначение: 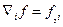, тогда

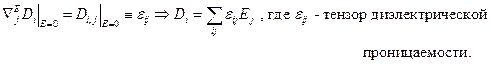
Аналогично вводятся тензоры:

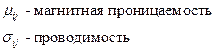
Для ферромагнетиков 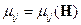- учёт нелинейности.

Неоднородные среды

Среды, для которых материальные характеристики ( 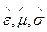) являются функциями координат.

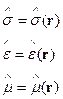
Т.е. характеристики трансляционно неинвариантны.

Введём понятие сплошной среды. Сплошная среда – это среда в каждой точке которой измерение материальных характеристик даёт не нулевой результат. Сплошная среда – это модель. В реальной среде имеются микро-пустоты, т.е. вещество локализовано в некоторых точках пространства. Чтобы перейти к сплошной среде, нужно усреднить микро-параметры по достаточно большому объёму.

Анизотропные среды

Анизотропные среды (свойства), это такие среды, свойства которых зависят от направления, в котором это свойство измеряется.

Пусть в каком-то направлении исследуются оптические свойства среды. Затем мы повернули направление исследования, и оптические свойства изменились, т.е. оптические свойства зависят от угла поворота.

Так как свойства меняются, то они неинвариантны относительно вращения. Этим свойством обладает всякая анизотропная среда.

Для тензоров 2-го ранга есть исключения:

Кубические системы описываются тензорами изотропного вида, т.е.

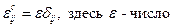
Монокристалл – есть однородная анизотропная среда.

Тензоры и их свойства.

Запись преобразований тензора 2-го ранга при вращении.

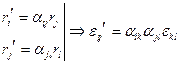
Пусть у нас есть монокристалл определённого вещества. Существует набор преобразований при которых его свойства инвариантны. Операции симметрии можно задать матрицами ортогональных преобразований

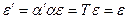
Оператор 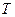принадлежит к симметрическим операторам. Итак, условие инвариантности:

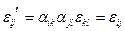
Для монокристалла орторомбической системы:

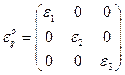
Оси выбираются к характерным направлениям в кристалле.

Для монокристаллов гексагональной системы:

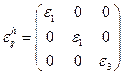
Для кубической: