Дәлелдеудің синтез тәсілі
1. ДК-ны АВ-ға параллель етіп жүргіземіз; яғни ДК | | АВ.
2. 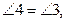 өйткені ДК | | АВ, мұнда ВС қиюшы.
өйткені ДК | | АВ, мұнда ВС қиюшы.
3. 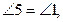 өйткені ДК | | АВ, мұнда АВ қиюшы.
өйткені ДК | | АВ, мұнда АВ қиюшы.
4. 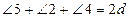 жазық бұрыш.
жазық бұрыш.
5. (2) және (3)-ге сәйкес; 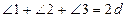 .
.
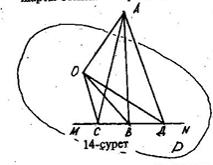
Теорема: Егер жазықтықтағы түзу көлбеудің табаны арқылы өтіп, оның сол жазықтықтағы проекциясына перпендикуляр болса, онда ол сол көлбеудің өзіне де перпендикуляр болады.
Берілген: 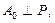
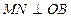 және MN түзуі р жазықтығында жатыр.
және MN түзуі р жазықтығында жатыр.
Дәлелдеу керек: 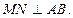
Қосымша MN түзуінің бойына В нүктесінің екі жағында жататындай ВС=ВД болатындай етіп С және Д нүктесін саламыз да, оларды А және О нүктелерімен қосамыз.
| Анализ: | Синтез: | |
1. 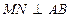 немесе немесе 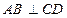 болсын. болсын. | 1. 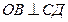 немесе немесе 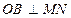 екені теореманың шарты бойынша белгілі. екені теореманың шарты бойынша белгілі. | |
2. Онда 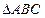 – тең бүйірлі, өйткені АВ-медиана, яғни АС=АД. – тең бүйірлі, өйткені АВ-медиана, яғни АС=АД. | 2. Онда 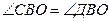 тік бұрыштар болғандықтан. тік бұрыштар болғандықтан. | |
| 3. Олай болса, ОС=ОД (өзара тең АС және АД көлбеулерінің проекциялары болғандықтан). | 3. Олай болса 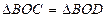 (тік бұрышты үшбұрыштардың ОВ катеті ортақ, ал ВС мен ВД катеттері өзара тең). (тік бұрышты үшбұрыштардың ОВ катеті ортақ, ал ВС мен ВД катеттері өзара тең). | |
4. Онда 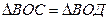 (ОВ ортақ, ал ОС=ОД және ВС=ВД болғандықтан. (ОВ ортақ, ал ОС=ОД және ВС=ВД болғандықтан. | 4. Онда ОС=ОД. | |
5. Мұнан 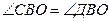 екені байқалады (тең үшбұрыштарда тең қабырғаларға қарсы жатқан бұрыштар болғандықтан және бұлар сыбайлас бұрыштар). екені байқалады (тең үшбұрыштарда тең қабырғаларға қарсы жатқан бұрыштар болғандықтан және бұлар сыбайлас бұрыштар). | 5. Мұнан АС=АД (проекциялары ОС мен ОД тең болғандықтан), яғни 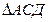 тең бүйірлі екені шығады. тең бүйірлі екені шығады. | |
6. Онда 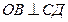 немесе немесе 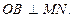 Ал бұл теореманың шарты бойынша берілген. Ал бұл теореманың шарты бойынша берілген. | 6. Онда 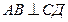 (АВ-тең бүйірлі үшбұрыштың медианасы болғандықтан биіктігі де болады), яғни (АВ-тең бүйірлі үшбұрыштың медианасы болғандықтан биіктігі де болады), яғни 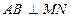 . . | |
|

ә) Қарсы жору арқылы дәлелдеу.
Біз математикада қарсы жору арқылы дәлелдеуді жиі кездестіреміз. Осы методпен жақынырақ танысайық.
Кейбір теоремалардың тікелей дәлелдеуі қиын болған жағдайда, оның орнына оған эквивалент керіге қарама-қарсы теореманы дәлелдейді. Бірақ әдетте, ол теореманы атап айтып жатпай-ақ, “қарсы жору арқылы дәлелдейік” дейді. Осы қарсы жору арқылы дәлелдегенде, шындығында біз керіге қарама-қарсы теореманы дәлелдейміз.
Бұл айтылғанды мысал арқылы түсіндірейік.
Теорема:Егер а және b түзулері с түзуіне перпендикуляр болса, онда олар қиылыспайды (a, b және c түзулерін бір жазықтықта деп қарастырып отырмыз).
Дәлелдеуі:а жәнеb түзулері бір Р нүктесінде қиылысқан деп қарсы жориық. Онда бір нүктеден (Р) бір түзуге (с) екі перпендикуляр жүргізілген болар еді. Бұл берілген нүктеден берілген түзуге тек бір ғана перпендикуляр түсіруге болады дегенге қайшы келеді. Демек, a және b түзулері қиылыспайды.
Біз шындығында: “Егер екі түзу (a, b) қиылысса, онда олардың ортақ перпендикуляры болмайды” деген керіге қарама-қарсы теореманы дәлелдедік.
Мектеп математика курсында теоремаларды дәлелдеу туралы мәселе көтерілгенде мынадай мәселелерге ерекше назар аударылуы керек:
1) теореманың мазмұнын түсіну;
2) теореманың шарты мен қорытындысын дәл анықтау;
3) дәлелдеудің идеясын білу;
4) дәлелдеуді жүргізу;
5) теореманың қажеттілігін, оның орны мен рөлін түсіну;
6) теореманы басқа теоремаларды дәлелдеу мен есептер шығаруда қолдану.
Сұрақтар:
1. Дәлелдеу;
2. Математиклық дәлелдеу;
3.Дәлелдеу силлогизмдер тізбегі
4. Математиклық дәлелдеу әдістері.

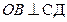 немесе
немесе