Расчет элементов нулевого и положительного колес

Вычертить три вида зубчатых колес, рассчитать по заданным модулю и делительной окружности элементы нулевого и положительного колес и монтажные размеры из зацепления в сборке. Расчеты сводятся в таб.1.

Примечание. При зацеплении корригированных колес угол зацепления в сборке находят по таблицам инволют, предварительно рассчитав по следующей форме:

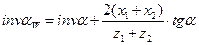
где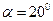

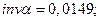
x₁, x₂ – коэффициент относительного смещения;

z₁, z₂ - число зубьев соответственно первого и второго колеса;

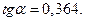
Проверка правильности расчетов

1. Радиусы окружностей впадин rf1, rf2 должны коснуться впадины соответствующего колеса.

2. Высоты зубьев нулевого и положительного колеса равны

h₁=h₂=2,25m

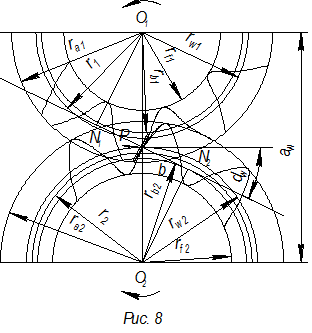
Построение картины зацепления

Цель работы

Ознакомление с зубчатым зацеплением и основными показателями его работы.

Объем работы

Согласно данным расчета (табл.1) зубчатого зацепления нулевого (x₁=0) и положительного колес (x₂>0) вычерчивается картина зацепления колес.

Порядок выполнения работы

1. Отложить на чистом листе ватмана межцентровое расстояние

a₁ = O₁O₂

2. Провести из центра О₁ окружности: основную, делительную, выступов r_a1 и впадин r_f1 первого колеса.

3. Провести из центра О₂ окружности: основную, делительную, выступов ra2 и впадин rf2 второго колеса.

4. Провести внутреннюю касательную к обеим основным окружностям. Из центров колес опустить перпендикуляры на проведенную линию. Основания перпендикуляров (точки касания) обозначить буквами N₁ и N₂, (N₁N₂ – теоретическая линия зацепления).

5. Обозначить точку пересечения линии N1N2 и линии центров – полюс зацепления буквой Р.

6. Провести через полюс зацепления перпендикуляр к линии центров. Заменить и записать угол зацепления в сборке 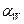. Сравнить с расчетным.

7. Провести начальные окружности, касающиеся друг друга в полюсе Р зацепления, r_w1, r_w2.

8. Отметить точки пересечения линии N₁N₂ с окружностями выступов буквами а и в – рабочая (активная) часть линии зацепления. Для правильности работы колес линия должна быть внутри N₁N₂, иначе может произойти заклинивание при работе колес.

9. Совместить центр заготовки с центром О1 и подвести зубцы нулевого колеса таким образом, чтобы боковой профиль среднего зуба касался полюса. Обратить внимание на то, что линия ав должна быть перпендикулярна этому боковому профилю. Обвести три зуба первого колеса.

10. Подобным образом вычертить зубцы второго колеса.

11. У зуба работает только та часть профиля, которая попадает на линию зацепления ав, т.е. часть, по которой происходит фактическое касание сопряженных зубьев. Она называется активным профилем. На зубьях, соприкасающихся в полюсе, утолщением линии отметить активный профиль зубьев. Для этого из центра О₁ сделать засечку на этом профиле радиусом аО₁, и из центра О₂ – радиусом О_2в.

12. Определить коэффициент перекрытия по формуле (табл.1)

КОЭФФИЦИЕНТ ПЕРЕКРЫТИЯ (продолжительность зацепления).

Одним из параметров, характеризующих правильность работы зубчатой передачи, является коэффициент перекрытия, который представляет собой отношение дуги зацепления к шагу, измеренному по той же окружности.

ДУГА ЗАЦЕПЛЕНИЯ это путь по начальной окружности, который проходит профиль зуба за время фактического его зацепления.

Для непрерывной передачи движения надо, чтобы дуга была больше, чем шаг. Тогда не успеет выйти из зацепления одна пара, другая войдет в зацепление, и какой-то период времени в зацеплении будут находиться две пары зубьев. Коэффициент перекрытия обозначается буквой 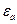, должен быть 1,1. Цифра после запятой показывает, какой процент времени в зацеплении находятся две пары. Чем больше этот процент, тем лучше, так как колеса работают более плавно, а нагрузка распределяется на две пары.

Если коэффициент перекрытия получится меньше 1,0, передача будет работать со стуком. Коэффициент перекрытия выражает также отношение зацепления к шагу по основной окружности.

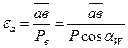
где ав – длина линии зацепления в мм.

РВ – шаг по основной окружности

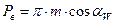
РАСЧЕТ ОСНОВНЫХ ПАРАМЕТРОВ НУЛЕВОГО И ПОЛОЖИТЕЛЬНОГО КОЛЕС

НАИМЕНОВАНИЕ	ОБОЗНАЧЕНИЕ	НУЛЕВОЕ КОЛЕСО	ПОЛОЖИТЕЛЬНОЕ КОЛЕСО
Число зубьев	z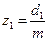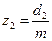
Диаметр основной окружности	dB		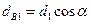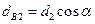
Угол профиля рейки			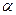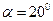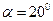
Шаг зацепления	P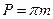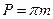
Коэффициент коррекции	х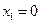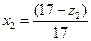
Абсолютное смещение инструмента	a		a=mx2
Толщина зуба по делительной окружности	S	S1=0,5P	S2=0,5Р+2mx2tg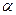
Угол зацепления в сборке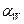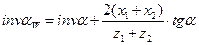
Межцентровое расстояние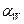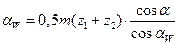
Радиус окружности впадин	rf	rf 1=r1-1,25m	rf 2=r2-1,25m+mx2
Радиус окружности выступов	ra	ra1 = aw - ( rf2 +0,25m)	ra2 = aw - ( rf1 +0,25m)
Коэффициент перекрытия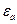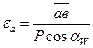

Контрольные вопросы

1. В чем состоит метод обкатки?

2. Нарисуйте исходный контур рейки.

3. Какие колеса называют нулевыми?

4. Каковы элементы зуба в нулевом колесе?

5. Покажите подрез зуба.

6. Какие колеса называют корригированными или исправленными?

7. Как получают положительные колеса?

8. Для чего производиться положительный сдвиг инструмента?

9. Что такое коэффициент коррекции?

10. Что такое абсолютный сдвиг инструмента? Как он определяется?

11. У каких зубьев толщина по делительной окружности больше?

12. Что называется эвольвентой круга?

13. Каково назначение основной окружности?

14. Перечислите элементы зубчатого колеса.

15. Что такое начальная окружность?

16. Что такое полюс зацепления?

17. Что называется межцентровым расстоянием?

18. Какие окружности называют делительными?

19. Что называется модулем зацепления? Его размерность.

20. Что такое inv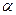

21. В каких передачах начальные окружности совпадают с делительными?

22. Каков физический смысл коэффициента перекрытия?

23. Что такое линия зацепления?

24. Какой профиль зуба является рабочим?

25. Что называется шагом зацепления?

26. Что называется окружностью впадин?

27. Что называется окружностью выступов?

28. На какие части полюс Р делит межосевое расстояние?