Дифференциальные уравнения в частных производных
Основная статья: Дифференциальные уравнения в частных производных
Дифференциальные уравнения в частных производных (УРЧП) — это уравнения, содержащие неизвестные функции от нескольких переменных и их частные производные. Общий вид таких уравнений можно представить в виде:
,
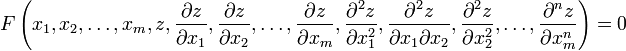где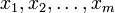 
— независимые переменные, а 
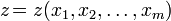— функция этих переменных.
Обыкновенные дифференциальные уравнения
Основная статья: Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения вида
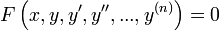или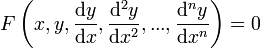 
,
где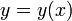 
— неизвестная функция (возможно, вектор функция ; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от независимой переменной 
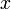, штрих означает дифференцирование по 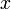. Число 
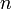называется порядком дифференциального уравнения.
6.ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ С ОСОБЕННОСТЯМИ В КОЭФФИЦИЕНТАХ- уравнение с частными производными, коэффициенты и свободный член к-рого на некоторых многообразиях из замыкания области их задания имеют разрывы первого рода или обращаются в бесконечность.
Типичными уравнениями такого типа являются, например, уравнение Лаврентьева - Бицадзе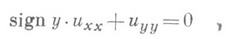 
и уравнение Эйлера - Пуассона-Дарбу
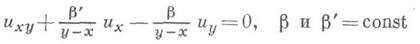
или
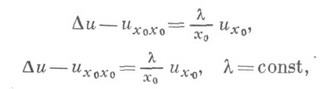
где D - оператор Лапласа по переменным х 1, . .., х п.
8
Дифференциальные уравнения
Задача 1. Найти общее решение дифференциального уравнения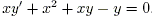 
Задача 2. Решить задачу Коши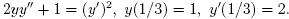 
Задача 3. Показать, что функция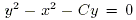 
является общим интегралом дифференциального уравнения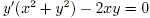 
Задача 4. Решить дифференциальное уравнение
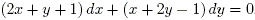
Задача 5. Решить дифференциальное уравнение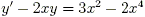 
Задача 6. Решить дифференциальное уравнение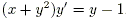 
Задача 7. Скорость остывания нагретого тела пропорциональна разности температур тела и окружающей среды. За 10 минут тело охладилось от 100 до 60 градусов. Температура среды постоянна и равна 20 градусам. Когда тело остынет до 25 градусов?
Задача 8. Решить дифференциальное уравнение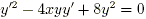 
Литература
Учебники
- В. И. Арнольд. Обыкновенные дифференциальные уравнения. М.: Наука, 1966.
- Л. С. Понтрягин Обыкновенные дифференциальные уравнения. М.: Наука, 1974
- Л. Э. Эльсгольц. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969.
- А. Н. Тихонов, Васильева А. Б., А. Г. Свешников. Дифференциальные уравнения, 4е изд., Физматлит, 2005.
- А. Н. Тихонов, А. А. Самарский. Уравнения математической физики. М.: Наука, 1972.
- А. Д. Полянин, В. Ф. Зайцев, А. И. Журов. Методы решения нелинейных уравнений математической физики и механики. М.: Физматлит, 2005.
- Чарльз Генри Эдвардс , Дэвид Э. Пенни. Дифференциальные уравнения и проблема собственных значений: моделирование и вычисление с помощью Mathematica, Maple и MATLAB = Differential Equations and Boundary Value Problems: Computing and Modeling. — 3-е изд. — М.: «Вильямс», 2007. — ISBN 978-5-8459-1166-7
- Х. Р. Латипов. Качественные исследование характеристик одного класса дифференциальных уравнений в целом. Т.: ФАН, 1993
- А. Ф. Филиппов Введение в теорию дифференциальных уравнений. — Изд. 2-е. — 2007. — 240 с. — ISBN 5354004160
- А. М. Ахтямов. Математика для социологов и экономистов. — М. : Физматлит, 2004.
Справочники
- Э. Камке. Справочник по обыкновенным дифференциальным уравнениям. М.: Наука, 1976.
- В. Ф. Зайцев, А. Д. Полянин. Справочник по обыкновенным дифференциальным уравнениям. М.: Физматлит, 2001.
- Э. Камке. Справочник по дифференциальным уравнениям в частных производных первого порядка. М.: Наука, 1966.
- В. Ф. Зайцев, А. Д. Полянин. Справочник по дифференциальным уравнениям с частными производными первого порядка. М.: Физматлит, 2003.
- А. Д. Полянин, В. Ф. Зайцев. Справочник по нелинейным уравнениям математической физики: Точные решения. М.: Физматлит, 2002 .
Заключение
В результате проведенной работы была раскрыта тема “дифференциальные уравнения второго порядка”, поставленная цель достигнута в полном объеме, выполнены следующие задачи:
1.Расмотрены основные понятия
2.Изучены линейные дифференциальные уравнения первого порядка
3.Изучены линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
4.Повторены обыкновенные дифференциальные уравнения
5.Найдены примеры и уравнения
В заключении хотелось бы отметить, что будущее экономики непосредственно зависит от Дифференциальных уравнений. Актуальность данной проблемы можно наблюдать как в модели Эванса, где непосредственно используются Дифференцированные уравнения, так и в современном производстве, зависящей от взаимодействия спроса и предложения.