Идеальное дифференцирующее звено

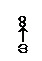Дифференциальное уравнение 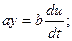определим передаточную функцию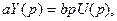

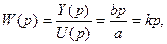
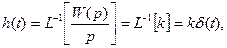
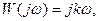
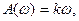
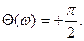
Пример1. Тахогенератор - генератор постоянного или переменного тока,

предназначенный для измерения скорости вращения механизмов.

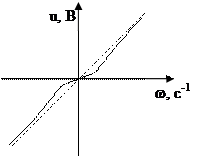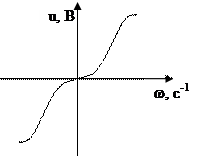Статическая характеристика ТГ Статическая характеристика ТГ

постоянного тока переменного тока.

Тахогенераторам постоянного тока свойственны пульсации из-за коллектора.

Высокий уровень помех и у тахогенераторов переменного тока.

Если пренебречь инерционностью тахогенератора, то, считая входом угол поворота вала, выходом напряжение, тахогенератор можно считать идеальным дифференцирующим звеном.

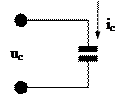При использовании ТГ в качестве датчика угловой скорости 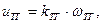в качестве преобразователя угла поворота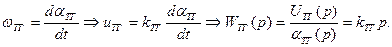

Пример2.

конденсатор – идеальное дифференцирующее звено.

Если u_c – вход, i_c – выход, то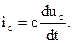

В преобразованиях Лапласа I_c(p)=CpU_c(p) Þ W(p)=I_c(p)/U_c(p)=kp,

где k=C.

Критерий Найквиста для систем с неустойчивой разомкнутой цепью.

Система с неустойчивой разомкнутой цепью

Более общий случай - знаменатель передаточной функции разомкнутой системы содержит корни, лежащие в правой полуплоскости. Появление неустойчивости разомкнутой системы вызывается двумя причинами:

1. Следствием наличия неустойчивых звеньев;

2. Следствием потери устойчивости звеньев, охваченных положительной или отрицательной обратными связями.

Xотя теоретически вся система в замкнутом состоянии может быть устойчивой при наличии неустойчивости по цепи местной обратной связи, практически такой случай является нежелательным и его надо избегать, стремясь использовать только устойчивые местные обратные связи. Это объясняется наличием нежелательных свойств, в частности появлением условной устойчивости, которая при имеющихся обычно в системе нелинейностях может в некоторых режимах привести к потере устойчивости и появлению автоколебаний. Поэтому, как правило, при расчете системы выбирают такие местные обратные связи, которые были бы устойчивыми при разомкнутой главной обратной связи.

Пусть характеристический многочлен D(p) разомкнутой системы имеет m корней с положительной вещественной частью.

Тогда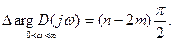

Вспомогательная функция 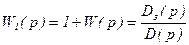при замене p®jw согласно принципа аргумента для устойчивых замкнутых систем должна иметь следующее изменение аргумента при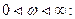

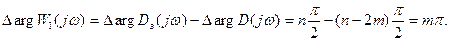
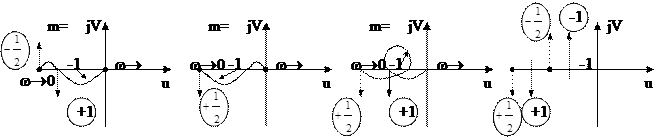
Формулировка критерия №3

Для устойчивости замкнутой системы, разомкнутая цепь которой неустойчива, требуется, чтобы амплитудно-фазовая характеристика разомкнутой цепи (с дополнением в бесконечности для систем с нулевыми и чисто мнимыми полюсами передаточной функции разомкнутой системы) охватывала точку (-1, j0) против часовой стрелки на угол mp, где m - число полюсов с положительной вещественной частью в передаточной функции неустойчивой разомкнутой цепи системы.