Зачет№1 по Линейной алгебре
1) Даны матрицы 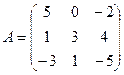 ’
’ 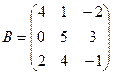
а) Построить матрицу С = 2А -3В+Ат +Е.
б) Найти произведение матрицы А на матрицу В.
в) Вычислить определители матрицы А и матрицы В. Убедитесь, что det(AB)=detA∙detB.
2) Найти А-1 и сделать проверку:
a) 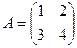 ; б)
; б) 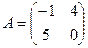 ; в)
; в) 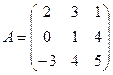
3) Каждую из следующих систем решить методом Крамера, Гаусса, матричным методом:
А) х + 2у + 3z = 14; б) 2x - 3y + z = 8;
2x + y – z = 1; 5x – y – z = 10;
3x + 2y + 2z = 13; x + 3y + 4z = 3.
4) Решите систему методом Гаусса:
2х1 + х2 – х3 + х4 = 1
3х1 – 2х2 + 2х3 – 3х4 = 2
5х1 + х2 – х3 + 2х4 = -1
2х1 – х2 + х3 – 3х4 = 4
5) Проверить линейную зависимость указанных векторов:
a) 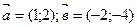 ;
;  б)
б) 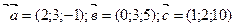 .
. 
6) 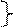
 Доказать, что векторы
Доказать, что векторы 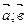 образуют базис в R3 и разложить по этому базису вектор
образуют базис в R3 и разложить по этому базису вектор 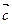
a) 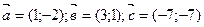
б) 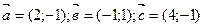
 6)Доказать, что векторы
6)Доказать, что векторы 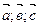 образуют базис в R3 и разложить по этому базису вектор
образуют базис в R3 и разложить по этому базису вектор
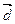 ,
, 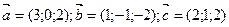
7)Вычислить скалярное произведение 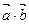
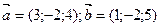
7) Найти косинус угла между векторами 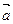 и
и 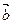
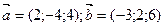
8) Даны векторы 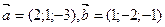
Найти норму вектора 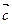 , если
, если 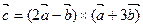
9) Найти площадь параллелограмма, построенного на векторах
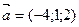 и
и 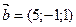
10) Даны вершины пирамиды
А(-4; -1; 2), В(-1; 0; 3), С(2; 2; 5), Д(3; -2; -1). Найти площадь всех граней пирамиды.
11) Вычислить смешанное произведение векторов 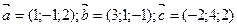 .
.
12) Найти объем параллелепипеда, построенного на векторах 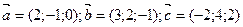
13) Установить, компланарны ли векторы 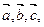 если
если 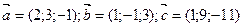 .
.
Зачет №2 по Линейной алгебре.
1) Проверить линейную зависимость указанных векторов:
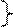
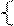
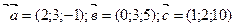
2) Векторы 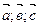 образуют базис в R3 , разложить по этому базису вектор
образуют базис в R3 , разложить по этому базису вектор 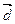
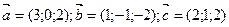
3) Вычислить скалярное произведение 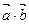
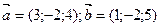
4) Найти косинус угла между векторами 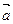 и
и 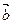
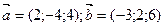
5) Даны векторы 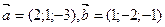
Найти норму вектора 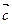 , если
, если 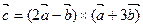
6) Найти площадь параллелограмма, построенного на векторах
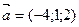 и
и 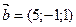
7) Даны вершины пирамиды
А(-4; -1; 2), В(-1; 0; 3), С(2; 2; 5), Д(3; -2; -1). Найти площадь грани АВС пирамиды.
8) Вычислить смешанное произведение векторов 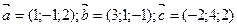 .
.
9) Найти объем параллелепипеда, построенного на векторах 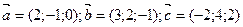
10) Установить, компланарны ли векторы 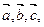 если
если 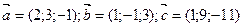 .
.
11) Даны матрицы 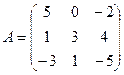 ’
’ 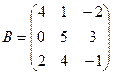
Построить матрицу С = 2А -3В+Ат +Е.
12) Найти произведение матрицы А на матрицу В и вычислить det(AB).
13) Найти А-1 и сделать проверку:
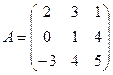
14) Решите систему:
х + 2у + 3z = 14;
2x + y – z = 1;
3x + 2y + 2z = 13;
15) Решите систему методом Гаусса:
2х1 + х2 – х3 + х4 = 1
3х1 – 2х2 + 2х3 – 3х4 = 2
5х1 + х2 – х3 + 2х4 = -1
2х1 – х2 + х3 – 3х4 = 4
Зачет№3
Задание 1
Вариант 1. Является ли линейным пространством множество всех непрерывных функций
Y=ƒ  (x), ƒ(x)>0 ?
(x), ƒ(x)>0 ?
Вариант 2. Образует ли линейное пространство множество всех непрерывных функций, заданных на [0;1] ?
Вариант 3.Образует ли линейное пространство множество всех многочленов третьей степени от переменной X, если заданные их суммы P3+Q3 и произведение на число 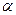 P3 ?
P3 ?
Вариант 4.Образует ли линейное пространство множество всех положительных чисел,
Если сумма чисел и произведение на число заданы обычным образом ?
Вариант 5 Образует ли множество всех векторов, лежащих на одной оси, линейное пространство, если сумма двух векторов 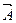 и
и 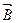 равно
равно 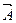 +
+ 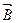 , произведение числа
, произведение числа 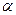 не
не 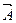 равно
равно 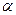
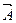 ?
?
Задание 2
Исследовать на линейную зависимость систему векторов 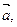
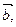
| Вариант | 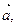 | 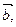 | 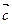 |
| (-2,1,5) | (4,-3,0) | (0,-1,10) | |
| (2,0,2) | (1,-1,0) | (0,-1,-2) | |
| (5,4,3) | (3,3,2) | (8,1,3) | |
| (1,1,1) | (0,1,1) | (0,0,1) | |
| (1,2,3) | (4,5,6) | (2,-1,3) |
Задание 3
Определить Размерность линейного пространства решений заданной системы 
 1. 3x1+x2-8x3+2x4+x5=0 2. x1+x2-10x3+x4-x5=0 3. 2x1-x2+2x3-x4+x5=0
1. 3x1+x2-8x3+2x4+x5=0 2. x1+x2-10x3+x4-x5=0 3. 2x1-x2+2x3-x4+x5=0
2x1-2x2-3x3-7x4+2x5=0 5x1-x2+8x3-2x4+2x5=0 x1+10x2-3x3-2x4+2x5=0
x1+11x2-12x3+34x4-5x5=0 3x1-3x2-12x3-4x4+4x5=0 4x1+19x2-4x3-5x4-x5=0
 |
 4. x1+2x2+x3+4x4+x5=0 5. 5x1-2x2+3x3-4x4-x5=0
4. x1+2x2+x3+4x4+x5=0 5. 5x1-2x2+3x3-4x4-x5=0
2x1-x2+3x3+x4-5x5=0 5x1-2x2+3x3-4x4-x5=0
x1+3x2-x3-6x4-x5=0 5x1-2x2+3x3-4x4-x5=0
. Задание 4
Дан вектор 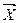 в базисе
в базисе 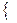 b
b 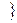 , найти его координаты в базисе
, найти его координаты в базисе 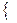 е
е 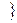
Вариант1 Вариант2 Вариант3 Вариант4 Вариант5
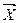 =(6, -1, 3)
=(6, -1, 3) 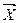 =(1, 3, 6)
=(1, 3, 6) 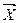 =(-1, 7, 14)
=(-1, 7, 14) 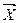 =(-3, 2, 4)
=(-3, 2, 4) 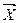 =(2, 4, 3)
=(2, 4, 3)
e1=b1+b2+2b3 e1=b1+b2+4b3 e1=b1+b2+8b3 e1=-b1+b2-b3 e1=-b1-b2
e2=2b1-b2 e2=4/3b1-b2 e2=8/7b1-b2 e2=b1-b2-b3 e2=b1+b2+0,5b3
e3=-b1+b2+b3 e3=-b1+b2+b3 e3=-b1+b2+b3 e3=-b1+2b2+b3 e3=-b1+b2+b3
Задание 5
Линейный оператор А в базисе e= 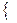 e1, e2, e3
e1, e2, e3 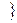 имеет матрице Ае. Найдите матрицу этого оператора в базисе b=
имеет матрице Ае. Найдите матрицу этого оператора в базисе b= 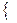 b1, b2, b3
b1, b2, b3 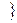 , если базисы
, если базисы 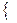 e
e 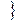 и
и 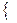 b
b 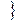 связаны заданными соотношениями.
связаны заданными соотношениями.
Вариант 1 Вариант 2 Вариант 3 Вариант 4 АE = 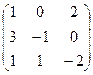 АE =
АE = 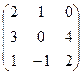 АE =
АE =  АE =
АE = 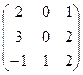
Вариант 5
АE = 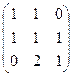
b1=e1-e2+e3 b1=2e1+3e2+e3 b1=e1+e2+e3 b1=e1+e2-6e3 b1=2e1+3e1+e3
b2=-e1+e2-2e3 b2=3e1+4e2+e3 b2=4e2+e3 b2=6/7e1-e2 b2=3e1+4e2+e3
b3=-e1+2e2+e3 b3=e1+2e2+2e3 b3=e1+2e3 b3=-e1+e2+e3 b3=e1+2e2+2e3
Задание 6
Найдите собственные векторы и собственные значения линейного оператора А, имеющего в некотором базисе е= 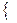 е1, е2, е3
е1, е2, е3  матрицу Ае
матрицу Ае
Вариант 1 Вариант 2 Вариант 3 Вариант 4 АE = 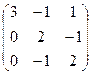 АE =
АE = 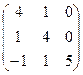 АE =
АE = 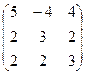 АE =
АE = 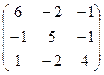
Вариант 5
АE = 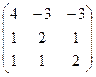
Задание 7
Убедитесь, что в R3 векторы а1, а2, а3 образуют базис. С их помощью постройте ортонормированный базис  е1, е2, е3
е1, е2, е3 
| Вариант 1 | а1=(2,1,2) | а2=(1,0,3) | а3=(-4,1,2) |
| Вариант 2 | а1=(-1,1,0) | а2=(0,1,1) | а3=(2,0,1) |
| Вариант 3 | а1=(-3, 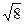 , , 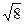 ) ) | а2=(5,-1,1) | а3=( 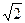 ,1,1) ,1,1) |
| Вариант 4 | а1=(2,2,1) | а2=(3-1,1) | а3=(4,-2,3) |
| Вариант 5 | а1=(2,4,0) | а2=(0,3,1) | а3=(-1,1,1) |
Задание 8
