Краткие сведения о матрицах и основные операции над ними

Матрица – таблица величин (элементов матрицы), записанных в определенной последовательности.

Различают следующие основные типы матриц: строчная, столбцевая, прямоугольная, квадратная, диагональная, единичная, нулевая, транспонированная.

Матрица ( 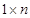), содержащая одну строку элементов, называется матрицей – строкой. Например, матрица 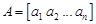является матрицей – строкой с 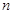элементами.

Матрица ( 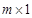), содержащая один столбец и 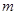строк, называется матрицей – столбцом.

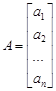
Матрица, содержащая 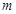строк и 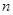столбцов, является прямоугольной матрицей и называется еще ( 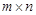) – матрицей, или матрицей порядка .

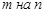Прямоугольная матрица, у которой число строк 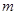равно числу столбцов 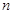, называется квадратной матрицей, или матрицей 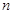-ого порядка.

Квадратная матрица, элементы которой, не лежащие на одной диагонали, равны нулю, называется диагональной матрицей.

Единичная матрица – диагональная матрица, у которой диагональные элементы равны единице.

Матрица, все элементы которой тождественно равны нулю, называется нулевой матрицей.

Транспонированная матрица получается из исходной в результате преобразования, при которой ее строки и столбцы меняются местами. Так, если исходная матрица

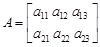
то транспонированная ей будет матрица

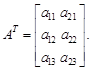
Суммой двух матриц А и В одного порядка ( 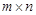) служит матрица С, элемент которой определяется как

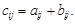
Пример: вычислить сумму двух матриц

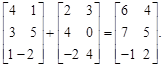
Разностью двух матриц А и B одного порядка ( 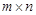) служит матрица D, элемент которой определяется как

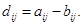
Умножение матриц. Пусть имеем две прямоугольные матрицы

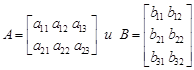
Произведение этих матриц:

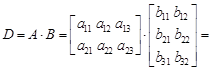
Правило умножения двух прямоугольных матриц А и В: элементы матрицы произведения D, расположенные на пересечении строки i и столбца j определяются в виде сумм попарных произведений из соответствующих элементов строки i матрицы А и столбца j матрицы В. Поэтому перемножение двух прямоугольных матриц А и В возможно, если число столбцов первой матрицы равно числу строк второй матрицы. При этом матрица, получаемая в результате перемножения, будет иметь число строк первой матрицы, а число столбцов – второй матрицы.

Пример. Вычислить произведение двух матриц

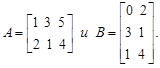
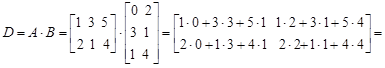
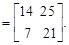
Следует помнить, что умножение матриц не обладает переместительным свойством. Так, если матрицы – множители А и В квадратные, одинакового порядка, то в общем случае .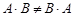

Обратная матрица. Это понятие возникает при решении матричных уравнений и в какой-то мере заменяет операцию деления, которая в непосредственном виде отсутствует в алгебре матриц. Обратная матрица существует только для квадратной неособенной матрицы, т.е. матрицы, определитель которой не равен 0.

Существуют различные способы нахождения обратной матрицы. Ниже приводится краткое описание получения обратной матрицы классическим методом, которым рекомендуется пользоваться при выполнении задачи первого контрольного задания.

Пусть дана квадратная неособенная матрица А n – ого порядка

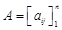
где 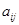- элемент матрицы А, расположенный на пересечении i-ой строки и j-ого столбца.

Матрицей, обратной А, будет являться матрица

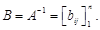
Элементы 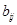обратной матрицы получаются в виде отношений соответствующих алгебраических дополнений 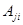(с обратными индексами) к определителю исходной матрицы А:

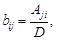
где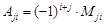

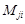- минор элемента 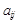исходной матрицы А, т.е. определитель (n-1) –ого порядка, который получается из исходной матрицы путем исключения строки j и столбца i.

Иначе обратную матрицу можно записать в следующем виде:

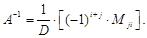
Пример. Дана матрица А третьего порядка

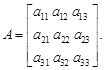
Для вычисления обратной матрицы В необходимо найти все миноры исходной матрицы. Пусть для обратной матрицы определяется элемент 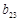. На месте этого элемента должен быть минор 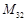исходной матрицы, определяемый путем исключения строки 3 и столбца 2, т.е.

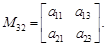
Аналогично определяются и все остальные миноры.

С учетом знаков элементов обратной матрицы, последняя получается в следующем виде:

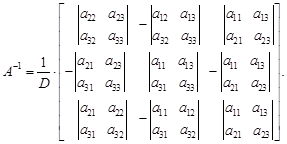
Определитель матрицы А находится по известным правилам.