Обчислення обернених матриць
В курсі вищої математики обернена матриця обчислюється за допомогою алгебраїчних доповнень. Але цей метод для комп'ютера непридатний. Тому розроблено метод "приклеювання" для обчислення обернених матриць [14]. Розглянемо приклад. Дано:

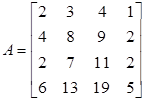 .
.
Перший крок.До матриці А "приклеюємо" одиничну матрицю справа: 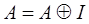 .
.
Маємо:
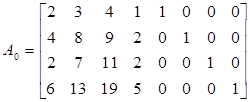 .
.
Перша ітерація.Перший рядок матриці А ділимо на діагональний член, тобто на 2 почленно. Отриманий рядок назвемо головним і запишемо його першим рядком матриці А1. Перший рядок виглядатиме так: (1 3/2 2 1/2 1/2 0 0 0). Ми тепер повинні утворити нулі у першому стовпці матриці А0, починаючи з другого рядка. Головний рядок множимо на (–4) і результат додаємо до другого рядка матриці А0. Отримаємо:
Другий рядок: (0 2 1 0 –2 1 0 0).
Головний рядок множимо на (–2) і додаємо почленно до третього рядка матриці А0. Отримаємо: (0 4 7 1 –1 0 1 0) (третій рядок).
Головний рядок множимо на (–6) і додаємо до четвертого рядка матриці А0. Маємо:
(0 4 7 2 –3 0 0 1) (четвертий рядок).
І остаточно маємо матрицю А1:
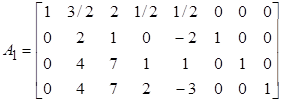 .
.
Наголосимо, що після першої ітерації матриці А1 перший стовпець являє собою перший стовпець одиничної матриці І.
Друга ітерація.Другий рядок матриці А1 почленно ділимо на діагональний член, тобто на 2 і результат наведемо головним рядком, записавши його другим рядком матриці А2:
(Другий рядок) (0 1 1/2 0 –1 1/2 0 0).
Тепер потрібно "утворити" нулі в другому стовпці. Отже, головний рядок множимо на (–3/2) і додаємо до першого рядка матриці А1 Отримаємо:
(Перший рядок) (1 0 0 1/4 5/4 –1 7 4 –3/4 0).
Множимо головний рядок на (–4) і додаємо почленно до третього рядка матриці А1 Отримаємо:
(Третій рядок) (0 0 5 1 3 –2 1 0).
Головний рядок множимо на (–4) і додаємо до четвертого рядка матриці А1. Отримаємо:
(Четвертий рядок) (0 0 5 2 1 –2 0 1).
Матриця А2 має такий вигляд:
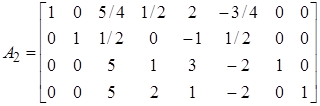 .
.
Після другої ітерації матриця А2 містить перший і другий стовпці одиничної матриці І.
Третя ітерація.Третій рядок матриці А2 ділимо на діагональний член, тобто на 5, і отримаємо третій головний рядок матриці А3. Маємо:
(Третій рядок) (0 0 1 1/5 3/5 –2/5 1/5 0).
Тепер звертаємо увагу на третій стовпець матриці А2, щоб в ньому сформувати третій стовпець одиничної матриці І. Третій головний рядок множимо на (–5/4) і почленно додаємо до першого рядка А2. Маємо:
(Перший рядок) (1 0 0 1/4 5/4 1/4 1/4 0). Третій головний рядок множимо на (–1/2), почленно додаємо до другого рядка А2. Отримаємо:
(Другий рядок) (0 1 0 –1/10 –13/10 7/10 –1/10 0).
Третій головний рядок множимо на (–5), почленно додаємо до четвертого рядка матриці А2. Маємо:
(Четвертий рядок) (0 0 0 1 –2 –1 1).
Остаточно маємо матрицю А3:
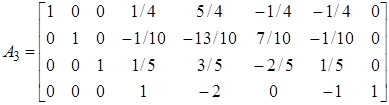 .
.
Після третьої ітерації перший, другий та третій стовпці матриці А3 являють собою перший, другий та третій стовпці одиничної матриці І.
Четверта ітерація. Четвертий рядок матриці А3 ділимо почленно, тобто на +1. Отримаємо четвертий головний рядок матриці A4, який множимо відповідно на (–1/4) і додаємо до першого рядка матриці А3. Маємо:
(Перший рядок) (1 0 0 0 7/4 –1/4 0 –1/4).
Головний рядок множимо на (+1/10) і додаємо до другого рядка А3. Маємо:
(Другий рядок) (0 1 0 0 –3/2 7/10 –1/5 1/10).
Головний рядок множимо на (–1/5) і додаємо до третього рядка матриці А3. Маємо: (Третій рядок) (0 0 1 0 1 –2/5 2/5 –1/5). Отримаємо матрицю A4, яка має такий вигляд:
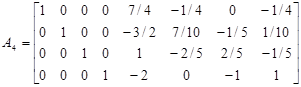 .
.
Після четвертої ітерації маємо:
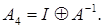
Отже, шукана обернена матриця А-1 знаходиться в п'ятому, шостому, сьомому та восьмому стовпцях матриці А4. Маємо:
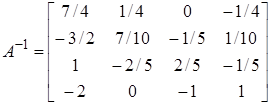 .
.
Якщо обчислення оберненої матриці виконані правильно, то справедлива рівність:
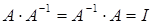 .
.
Перевірка:
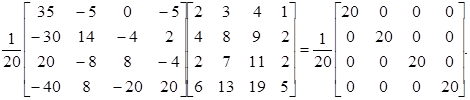
Обернена матриця знайдена правильно.
Запишемо програму мовою Turbo Pascаl «abba» та мовою BASIC «ABC» для обчислення оберненої матриці, зауваживши, що ми будемо вводити в пам’ять комп’ютера матрицю А0=АÅІ.
Program abba;
Const m=4; n=8; Label 2,3,4, 99;
Type g1= array [1..m,1..m] of real;
q2=ar ray [1..m,1..m] of real;
Var AÆ,A1,A2,A3,A4: q2;A,A11,l1:q1;
I, j, k: intger; S: real;
Begin
For i:=1 to m do begin
For j:=1 to n do begin
Writeln ( ’ Введіть АÆ[i,j]= ’);
Readln (AÆ[i,j]); end; end;
Writeln (перша ітерація);
For j:=1 to m do
A1[1,j]:=AÆ[1,j]/AÆ[1,1];
For i:=2 to m do begin
For i:=1 to n do begin
A1[1,j]:=AÆ[i,j]-A1[1,j]*AÆ[i,1]
End; end;
Writeln (друга ітерація);
If(A1[2,2]=Æ) then goto 2;
For j:=1 to n do
A2[2,j]:=AÆ[2,j]/AÆ[2,2];
For i:=1 to m do begin
For j:=1 to n do begin
If(i=2) then i:=i+1;
A2[i,j]:=A1[i,j]-A2[2,j]*A1[i,2]; end;end;
Writeln (’ Третя ітерація ’);
If(A2[3,3]=Æ) then goto 3;
For j:=1 to n do
A3[3,j]:=A2[3,j]/A2[3,3];
For i:=1 to m do begin
For j:=1 to n do begin
A3[i,j]:=A2[i,j]-A3[3,j]*A2[i,3]; end;end;
Writeln (’ Четверта ітерація ’);
If(A3[4,4]=Æ) then goto 4;
For j:=1 to n do
A4[4,j]:=A3[4,j]/A3[4,4];
For i:=1 to m-1 do begin
For j:=1 to n do begin
A[i,j]:=A3[i,j]-A4[4,j]*A3[i,4]; Еnd;Еnd;
For i:=1 to m do begin
For j:=1 to m do begin
A11[i,j]:=A4[i,j+m];
A[i,j]:=AÆ[ij];end; end;
{А11 – обернена матриця; А- дана матриця}[i,j] [ij] [i,j] [i,j] [i,j]
for i:=1 to m do begin
for i:=1 to m do begin
Writeln (`a11[.ij.]=` , A1[ij]:1Æ:4); end;end;
Writeln (’ Перевірка ’);
For i:=1 to m do begin
For j:=1 to m do begin
S:=Æ;
For k:=1 to m do begin
S:=S+A[i,k]*A11[kj];end;
II[i,j]:= S; Writeln (`II, [`,ij],` ]=`, I1[i,j]); end;end;goto 99;
2: Writeln (` A1[2,2]=Æ` ); goto 99;
3: Writeln (` A2[3,3]=Æ` ); goto 99;
4: Writeln (` A3[4,4]=Æ` );
99: End.
Програма "ABC":
05 PRINT"……….PROGRAM "ABC……….."
10 REM ОБЕРНЕНА МАТРИЦЯ +1
20 INPUT N,M
30DIM
Al(M,N),A2(M,N),A3(M,N),A4(M,N),A0(M,N)A0(M,N),A(M,N)
31 REM ЗАПИС МАТРИЦІ +ОДИНИЧНА
40 FOR 1=1 TO M
50 FOR J=1 TO N
60 PRINT "A0(“І”, “J”)=”
70 INPUT AO(I,J)
80 NEXT J
90 NEXT I
100 REM ПЕРША ІТЕРАЦІЯ
110 FOR J=l TO N
120 Al(l,J)=A0(l,J)/A0(l,l)
130 NEXT J
140 FOR І=2 TO M
150 FOR J=l TO N
160 A1(I,J)=AO(I,J)-A1(1,J> A0(U)
170 NEXT J
180 NEXT І
190 REM ДРУГА ІТЕРАЦІЯ
200 IF Al(2,2)-0 GOTO 661
210 FOR J=l TO N
220 A2(2,J)-A1(2,J)/A1(2,2)
230 NEXT J
240 FOR І=1 TO M
250 FOR J=l TO N
260 IF 1=2 THEN І=І+1
270 A2(U)-A1(I,J)-A2(2,J)* A1(I,2)
280 NEXT J
290 NEXT І
300 REM ТРЕТЯ ІТЕРАЦІЯ
310 IF A2(3,3)=0 GOTO 662
320 FOR J=l TO N
330 A3(3,J)=A2(3,J)/A2(3,3)
340 NEXT J
350 FOR І=1 TO M
360 FOR J=l TO N
361 IF І=3 THEN І=І+1
370 A3(I,J)=A2(I,J)-A3(3,J)* A2(I,3)
380 NEXT J
390 NEXT I
400 REM ЧЕТВЕРТА ІТЕРАЦІЯ
410 IF A3(4,4)=0 GOTO 663
420 FOR J=l TO N
430 A4(4,J)=A3(4,J)/A3(4,4)
440 NEXT J
450 FOR 1=1 TO M-l
460 FOR J=l TO N
470 A4(I,J)=A3(I,J)-A4(4,J)* A3(I,4)
480 NEXT J
490 NEXT I
500 FOR І=1 TO M
510 FOR J=l TO N
520 A0(I,J)=A4(I,J+M)
530 A(I,J)=A0(I,J)
531 PRINT “A0(“І”,“J”)=”;A0(I,J)
540 NEXT J
550 NEXT I
560 FOR І=1 TO M
570 FOR J=l TO N
590 REM ПЕРЕВІРКА A^-1 * A=l
600 A0(I,J)=0
610 FOR K=l TOM
620 А0(І,J)=А0(І,J)+А(І,К)* A0(K,J)
640 NEXT К
641 PRINT “A0(“І”,“J”)=”;A0(I,J)
650 NEXT J
660 NEXT I
661 PRINT “Al (2,2)=0”
662 PRINT “A2(3,3)=0”
663 PRINT “A3(4,4)=0”
680 END
