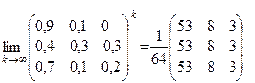Властивості стохастичних матриць

Визначення: Матриця D = P - I, де I - одинична матриця того ж порядку, що і Р, називається динамічною матрицею D= ||d_ij||,

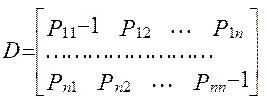(2.6).

Причому її елементи 0 < d_ij < 1, i = j; -1 < d_ii < 0 i = =1, ... , n

Тоді рівняння (3) можна переписати у вигляді

P(k) - P(k-1) = P(k-1) × D (2.7)

де (2.7) матрична форма запису системи рівнянь у кінцевих різницях ймовірностей переходу в однорідному марківському ланцюзі на k-ому кроці.

ВЛАСТИВОСТІ СТОХАСТИЧНИХ МАТРИЦЬ І ДЕЯКІ ЇХ РІЗНОВИДИ.

1. Якщо Р - стохастична матриця, то і P^(k) = P × P× ... ×P - стохастична.

2. Якщо всі рядки Р однакові, то P^(k) = Р.

3. Якщо

Р = 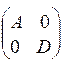(2.8),

де А та D - квадратні підматриці, то система із станів, що відповідають А, не перейде ніколи у стан, що відповідає D і навпаки. Р у цьому випадку називається такою, що розкладається, а дві розглянуті множини станів замкнутими.

4. Якщо

Р = 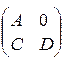(2.9),

де А, С, D - квадратні підматриці, то при Р^(k) можливість того, що система буде знаходитися в одному з станів, що відповідають D, не зростає. Перехід із стану D у А можливий, зворотне ж не вірне. Стани, що відповідають D називаються такими, що не повертаються.

Аналогічна властивість справедлива і для

Р = 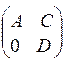(2.10)

Причому Р^(k), k -ціле > 0, зберігає вигляд Р.

У випадку (2.9) і (2.10) матрицю Р також називають такою, що розкладається.

5. Якщо

Р = 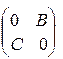(2.11),

де B, С - квадратні підматриці, то Р^(2m) дадуть матрицю вигляду (2.8), а Р^(2m+1) - вигляду (2.10).

Система буде по черзі переходити від станів, що відповідають В, до станів, що відповідають С та навпаки; така система називається періодичною.

Ергодична властивість ланцюгів Маркова.

Перехідний режим

Дуже істотною є ергодична властивість відповідно до якої існує граничний, або сталий, режим марковського процесу. Наступна теорема Маркова формулює цю властивість для ланцюгів Маркова.

Теорема: Якщо матриця переходу Р не являється такою, що розкладається або періодичною, то

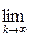P(k)=P( 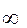)=Р (2.12),

де Р = (P₁, P₂, ... , P_n), (P_m> 0), тобто ймовірності станів прагнуть до граничних значень P₁, P₂, ... , P_n, що не залежить від початкового розподілу Р(0). У цьому випадку система статично стійка і має ергодичну властивість, а матриця переходу Р - ергодичною.

Сталим режимом називається режим переходу, що відповідає вектору Р( ) у випадку, коли система має ергодичну властивість. Всякий інший режим називається перехідним. У перехідному режимі Р(k) (для дискретного випадку) або Р(t) (для безупинного випадку) являється функціями часу.

Якщо існує сталий режим, то його ймовірностні стани знаходяться із розв’язання матричного рівняння

Р( 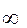) = Р( 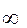)´P(2.13)

або

Р( 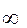)´D = 0 (2.14)

Можна показати, що якщо Р ергодична, то

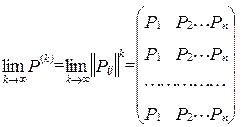(2.15 )

тобто при достатньо великому k усі рядки P^(k) будуть близькі до граничного вектора Р( ) = (P₁, P₂, ... , P_n).

Яким би не був вектор початкових станів Р(0), завжди при достатньо великих k P(k) = (P₁, P₂, ... , P_n).

Таким чином, якщо Р - ергодична, то система

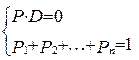(2.16 )

має єдине рішення.

Приклад 6. Нехай є 3 конкуруючих предмети споживання (продукти) В₁, В₂, В₃. З метою визначення попиту на ці продукти провадиться привселюдне опитування. Спочатку клієнтів опитують про те, яким із продуктів В₁, В₂, В₃ вони користуються. Нехай частки (або частоти) клієнтів утворилися Р₁(0)=0,5; Р₂(0)=0,2; Р₃(0)=0,3. Через місяць клієнтів опитують, чи користуються вони старим продуктом, наприклад В₁ або перейшли до нових, В₂ або В_3. При цьому нехай утворилися такі частоти P_ij (i, j = 1, 3), що відображають ймовірності переходу із станів S₁, S₂, S₃, де S_i - користування продуктом B_i (i = 1, 2, 3), що утворюють матрицю переходу

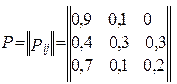
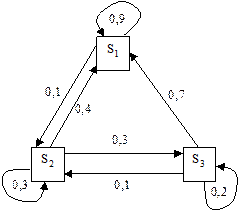Якщо поведінка клієнтури не змінюється з часом, то маємо стаціонарний ланцюг Маркова з матрицею переходу Р і графом переходів, мал.6. Так як Р не змінюється (за припущенням), то це однорідний марковський ланцюг.

Мал.6

Знайдемо сталий режим переходів. Так як матриця Р така, що не розкладається і не періодична, то за теоремою Маркова він існує. Для його визначення лишаємо і вирішуємо рівняння (2.16). Динамічна матриця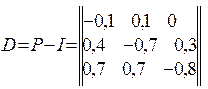

Система рівнянь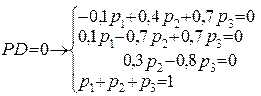

p₁+p₂+p₃ = 1

p = (p₁; p₂; p₃)

Вирішуючи цю систему, одержуємо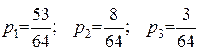

Отже,